Applichiamo il teorema della
media a
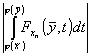
.
Poiché 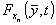 è positiva e continua, e C è compatto si ha che il
minimo di
è positiva e continua, e C è compatto si ha che il
minimo di 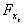 è ancora positivo.
è ancora positivo.
Quindi:
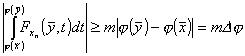 con
m>0.
con
m>0.
Dunque:
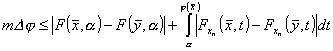
e, introducendo una particolare notazione
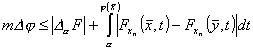 .
.
Per la relazione
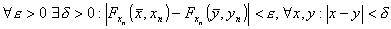
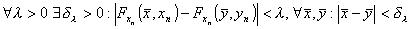 .
.
Questo implica che:
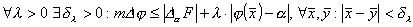 ,
,
poiché anche
F è uniformemente continua (si ripete
per essa il discorso fatto per
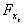
) si ha:
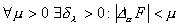 se
se 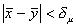 .
.
Posto
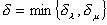
,
possiamo concludere che
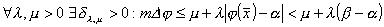 se
se 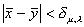 ,
,
e poiché
m>0:
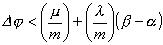 se
se 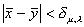 .
.
La precedente disuguaglianza
è valida per ogni valore di
l
e m.
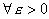
scelti
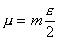
e
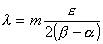
possiamo concludere che
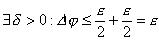
cioè
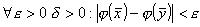 se
se 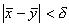
quindi
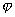
è continua.
Proviamo che le derivate
prime di
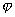
sono continue, cioè che
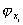
con
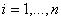
e
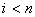
perché
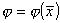
.
Indichiamo 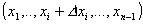 con
con 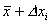 (in
altre parole
(in
altre parole 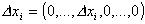 ). Supposto di considerare solo incrementi per cui rimaniamo nel disco
W
in cui è definita la
). Supposto di considerare solo incrementi per cui rimaniamo nel disco
W
in cui è definita la 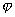 si ha:
si ha:
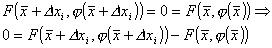
è positiva e continua, e C è compatto si ha che il
minimo di
è ancora positivo.
con
m>0.
con
(in
altre parole
). Supposto di considerare solo incrementi per cui rimaniamo nel disco
W
in cui è definita la
si ha: