Sería útil, a fin de comprender las splines, si tuviéramos un ejemplo donde pudiéramos practicar manipulando puntos y tipos de splines y ver cuales son los efectos. Así que, ¡hagamos uno! Ahora que sabemos como crear un torno básico, será fácil (ver fichero lathdem2.pov):

#include "colors.inc"
camera {
        orthographic
        up <0, 5, 0>
        right <5, 0, 0>
        location <2.5, 2.5, -100>
        look_at <2.5, 2.5, 0>
       }
/* Definir los puntos de control que serán usados */
#declare Red_Point    = <1.00, 0.00, 0>;
#declare Orange_Point = <1.75, 1.00, 0>;
#declare Yellow_Point = <2.50, 2.00, 0>;
#declare Green_Point  = <2.00, 3.00, 0>;
#declare Blue_Point   = <1.50, 4.00, 0>;
/* Hacer visibles los puntos de control */
cylinder { 
          Red_Point, Red_Point - 20*z, .1
          pigment { Red }
          finish { ambient 1 }
         }
cylinder {
          Orange_Point, Orange_Point - 20*z, .1
          pigment { Orange }
          finish { ambient 1 }
         }
cylinder { 
          Yellow_Point, Yellow_Point - 20*z, .1
          pigment { Yellow }
          finish { ambient 1 }
         }
cylinder {
          Green_Point, Green_Point - 20*z, .1
          pigment { Green }
          finish { ambient 1 }
         }
cylinder { 
          Blue_Point, Blue_Point- 20*z, .1
          pigment { Blue }
          finish { ambient 1 }
         }
/* Algo para hacer aparecer la curva */
lathe {
       linear_spline
       5,
       Red_Point,
       Orange_Point,
       Yellow_Point,
       Green_Point,
       Blue_Point
       pigment { White }
       finish { ambient 1 }
      }

Ahora, retomamos el aliento. Vemos que tiene una apariencia un poco rara, pero con algunas simples explicaciones, podremos ver fácilmente qué es lo que hace todo esto.

En primer lugar decir que estamos usando la cámara ortográfica. Si aún no hemos leído nada sobre ella, aquí hay un breve resumen: traza la escena plana, eliminando la distorsión de la perspectiva para que, en una vista lateral, los objetos tengan la misma apariencia que si hubieran sido dibujado en un plano de papel (como en la vista lateral de un modelador o programa de CAD). Hay varios usos para este nuevo y práctico tipo de cámara, pero aquí nos permitirá ver nuestro torno y cilindros como si fueran una sección transversal de la curva que forma el torno, más que el torno en sí mismo. Para reforzar el efecto hemos eliminado el sombreado con el acabado ambient 1 que, en efecto también elimina la necesidad de una fuente de luz. También hemos posicionado esta particular vista lateral para que el punto <0, 0> aparezca en la esquina inferior izquierda de nuestra escena.

A continuación hemos declarado un conjunto de puntos. Nótese que hemos usado vectores de tres componentes para estos puntos, en lugar de los vectores de dos que solemos usar en un torno. Esta es una excepción que ya mencionamos antes. Cuando declaramos un punto 3D y lo usamos en un torno, este solo usa las dos primeras componentes del vector y la tercera componente es ignorada. Esto es práctico aquí, ya que hace posible este ejemplo.

Ahora hacemos dos cosas con los puntos declarados. Primeros los usamos para colocar cilindros de pequeño diámetro con las bases apuntando hacia la cámara. Entonces volvemos a usar esos mismos vectores para determinar el torno. Ya que intentar declarar vectores en 2D puede ocasionar resultados no esperados y no es lo que necesitan nuestras declaraciones de cilindros, podemos aprovechar la tendencia del torno a ignorar la tercera componente poniendo la coordenada z a 0 en los vectores en 3D.

El resultado final es: cuando trazamos este código, vemos un torno de color blanco contra un fondo negro mostrándonos la forma de la curva que hemos declarado y las bases circulares de los cilindros nos muestran nuestros puntos de control sobre el plano xy. En este caso, es muy simple. La spline lineal ha sido usada de forma que nuestra curva está compuesta por una serie de líneas conectando los puntos. Ahora cambiamos las declaraciones de Red_Point y Blue_Point de la siguiente forma (ver fichero lathdem3.pov).

#declare Red_Point  = <2.00, 0.00, 0>;
#declare Blue_Point = <0.00, 4.00, 0>;

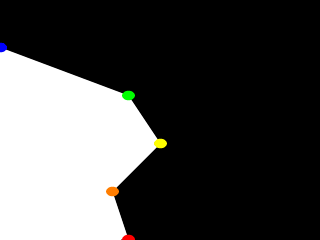
Trazamos de nuevo y lo que podemos ver es que los segmentos rectos se han movido para acomodarse a las nuevas posiciones de los puntos rojo y azul.

Vamos a intentar algo distinto. Primero cambiamos los puntos por estos otros (ver fichero lathdem4.pov).

#declare Red_Point    = <1.00, 0.00, 0>;
#declare Orange_Point = <2.00, 1.00, 0>;
#declare Yellow_Point = <3.50, 2.00, 0>;
#declare Green_Point  = <2.00, 3.00, 0>;
#declare Blue_Point   = <1.50, 4.00, 0>;

Ahora vamos a la declaración del torno y cambiamos linear_spline por quadratic_spline. Trazamos de nuevo y ¿qué tenemos? Bien, esta vez hay varias cosas que comentar. Primero, vemos que, en lugar de líneas rectas, tenemos arcos redondeados conectando los puntos. Estos arcos están formados a partir de curvas cuadráticas, de manera que ahora nuestro torno parece mucho más interesante. También vemos que Red_Point no está conectado a la curva. ¿Qué ha pasado?

Bien, mientras que cualquier pareja de puntos puede determinar una línea recta, se necesitan tres para determinar una curva cuadrática. POV-Ray no solo tiene en cuenta los dos puntos a ser conectados, si no también el punto que los precede para determinar la fórmula de la curva cuadrática que será usada para conectarlos. El problema está al principio de la curva. Más allá de su primer punto no hay punto previo. Así que necesitamos declarar uno. Por lo tanto, cuando se usa una spline cuadrática, debemos recordar que el primer punto que especificamos solo está allí para que POV-Ray pueda determinar la curva para conectar los dos primeros puntos. No se mostrarán como parte de la curva.

Solo hay una cosa más acerca de este ejemplo. A pesar de que nuestra curva está formada ahora por líneas redondeadas, las transiciones entre estas líneas son... bueno, un poco picadas. Parece que las líneas hubieran sido conectadas en los puntos de forma equivocada. Dependiendo de lo que intentemos hacer, esto puede ser aceptable, o podemos desear una forma más redondeada. Afortunadamente tenemos otra opción.

La spline cuadrática necesita más tiempo de trazado que la lineal. La fórmula matemática es más compleja. Más tiempo necesita aún la spline cúbica, aunque para una figura realmente redondeada, esta es la única opción. Volvemos a nuestro ejemplo y reemplazamos quadratic_spline por cubic_spline (ver archivo lathdem5.pov). Trazamos una vez más y vemos lo que tenemos.

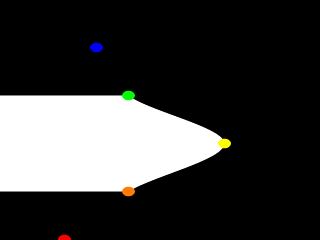
Mientras que una spline cuadrática necesita tres puntos para determinar la curva, una cúbica necesita cuatro. Así que, como esperábamos, el punto azul ha dejado de formar parte de la curva, como antes pasó con el punto rojo. Ahora el primer y el último punto de la curva son solo puntos de control para determinar las curvas entre los restantes puntos. Pero echemos un vistazo a las transiciones desde el punto naranja hasta el punto amarillo y después hasta el verde. Ahora, en lugar de parecer equivocados, los segmentos forman una sola curva completamente redondeada.

El concepto de las splines es algo útil y necesario, que se volverá a ver de nuevo en los objetos prisma y polígono. Con un poco de práctica podemos aprenderlo a usar rápidamente.