Untitled

Welcome to IMO Question Library
All questions here are in IMO (International Mathematical Olympiad) format.Answers of each questions will be posted in this page some days after the questions are posted.If anyone who would like to have an answer first,just contact me by e-mail:

As it is difficult to give all answers of the questions by myself,you are always welcomed to send me answer if you can solve it. Questions that I don't have the answer will have the sign: <!!> I need your help for all these questions.Send the complete answer to me by mail :

Past Question ~Questions~ 2/6/98 Answer to be posted on 6/6/98 Number 1:

Let a,b are positive number. n is a natural number greater or equal to 2
Prove:
[(a+b)/2]^n 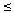(a^n+ a^(n-1)b+.....+b^n)/(n+1)

Number 2: Let A1A2......An be a regular polygon with sides of the same length.The polygon is inscribed inside a circle with center O, and with radius r.
P is a point on the extension of OA1.
Prove that:
PA1 x PA2 x............xPAn= OP^n - r^n

ANSWER Of Number 1 (2/6/98)
Let x= a/b
then, [(x+1)/2]^n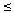

(x^n+x^(n-1)+.......+1)/(n+1)
when n=2,
[(x+1)/2]^2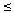

(x^2+x+1)/3
<=>3x^2+6x+3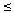

4x^2+4x+4
<=> 0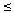

(x-1)^2
it is true for n=2
let n=(k-1) is true(k>=3)
when n=k,
as, x^(k-i)-1 and x^i -1 must have same sign or all of them are zero.
where i= 1,2,3,.......,k-1
so ,0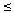

(x^(k-i)-1)(x^i -1)
ie,x^k +1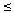

x^(k-i) +x^i
so,

add (k+1)(x^k+1)+2k(x^(k-1)+.....+x) at both side.
we get [x^k +2(x^(k-1)+....+x)+1]/2k
=[(x^(k-1)+....+x+1)/k ][(x+1)/2]

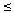[ [(x+1)/2]^(k-1)] [ (x+1)/2]

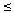(x^n+x^(n-1)+.......+1)/(n+1)

so ,by MI ,it's true for n>or=2
QED

ANSWER Of Number 2 (2/6/98)
Let A1,A2,.......An be n points on a Argand diagram and let them be the
roots of the equation: z^n = r^n .Also let P be a real number a represented on the Argand
diagram.O is the origin of the Argand diagram.
PA1 x PA2 x.........xPAn
= | a - A1|x.........x|a- An|
= | a ^n - A1 x A2 x.......x An |
= | a^n - r^n|
so PA1 x PA2 x............xPAn= OP^n - r^n

ANSWER of Number 2 (31/5/98)