VECTORS AND FORCES
III. Elevators and Gravity
Before you start, it would be most helpful if you understood what weight and
gravity is about (see: Weight,
Mass and Gravity).
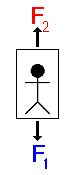 |
When you're standing still, there is actually a force pushing you up
(remember Newton's Third Law of Motion?) It doesn't matter if you're standing on
the grass or in a motionless lift, you will experience 2 forces: Gravity
and a reactive force. The reactive
force only exists if there is another force present.
The 2 forces can be combined to find the resultant force
(daya paduan).
F2
+ (- F1)
= F
(Remember, they are in opposite directions so one
has to be negative!) |
To distinguish between the different forces in the
following examples, let's write F2
as R. F1
is Weight, so let's write is as mg
R
- mg
= F
When the elevator is still, the person inside is not accelerating (a
= 0). Therefore:
| R
- mg |
=
ma |
| R
- mg |
=
m(0) |
| R
- mg |
=
0 |
| R |
=
0
+ mg |
| R |
=
mg |
So when standing still, R
= mg
That makes sense, doesn't it? If you're being
forced downwards by
gravity, you need an upwards
force that has the same magnitude (strength) to prevent your from moving. If one
of the forces is greater than the other, you will start moving in that
direction.
When the elevator is accelerating downwards, the
acceleration has a negative value (up is positive)
| R
- mg |
=
m(-a) |
| R
- mg |
=
-ma |
| R |
=
-ma
+ mg |
| R |
=
mg
- ma |
So when accelerating downwards, R
= mg
- ma<
In the 1st equation,
R is the same as
mg. But now, R
is LESS than mg.
(The equation says "mg MINUS something," which means the value of R is reduced)
This makes sense: The upwards force is not strong enough to cancel out the
downwards force, which is why the lift accelerates downwards.
When the elevator is accelerating upwards, the
acceleration has a positive value.
So when accelerating upwards, R
= mg
+
ma
Now, R
is GREATER than mg.
(The equation says "mg PLUS something," which means the value of R is increased)
This makes sense: Some of the upwards force has to be greater than the downwards
force in order to lift an objectThe upwards force is not strong enough to cancel
out the downwards force, which is why the lift accelerates downwards.
Ok, we've dealt with acceleration. What about
moving up/down with constant velocity (halaju seragam)? Well, remember
that there is no acceleration here, so R
= mg as if the lift was not moving
Important note: No extra force is needed to
keep an object moving at a constant velocity. Inertia causes it to
continue moving, even when there is no more force involved.
Page: 1 | 2 | 3
The Notes Portal Home
