 |
Remember Case 6 from Section
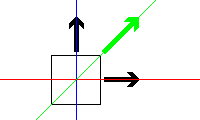
I? When the box is pulled to the right and up, it's as if
there was only one force pulling the box diagonally. Therefore, we say
that the diagonal arrow is the resultant force
(daya paduan) of the 2 original forces.
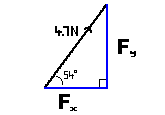
Similarly, if the box was pulled diagonally by only 1 force, that force can be separated into 2 components (dileraikan kepada 2 komponen): The horizontal component (komponen ufuk) and the vertical component (komponen tegak) |
|
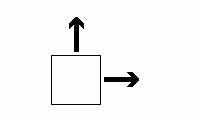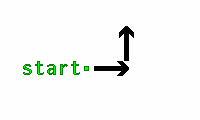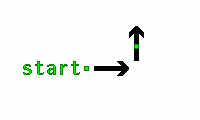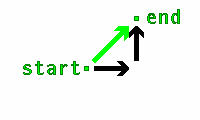
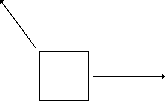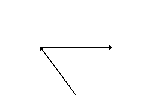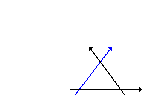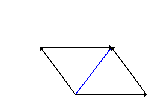
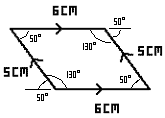
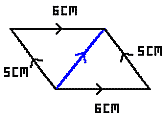
When given two or more forces, you can work out the resultant force by rearranging the arrows. Line them up so to form a continuous chain, starting from the 'tail' of one arrow and following their directions to the end. Draw a line from the start to the end, and that line is your resultant force.
|
|