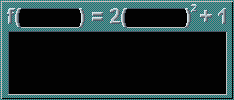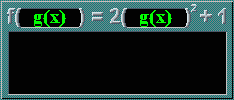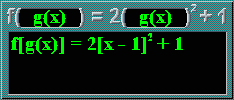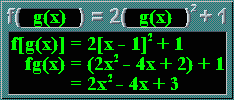

FUNCTIONS
II. Compound Functions
If you can take a simple number and put it into a function, you can also
take a function and put it into another function. Consider these:
f(x) = 2x2 + 1
g(x) = x - 1
If you put 3 into Function f(x), you get f(3) = 19. If you put 3 into Function g(x), you get g(3) = 2.
Now before we continue, let's pause for a while and consider what an 'equal' sign means. In the above situation, you can say that "f(3)" is the same as "19". If you write "2" on a piece of paper, I know that you are talking about "g(3)". When I mention "x - 1", you will know that I am talking about "g(x)".
So what does this mean? It means... you can substitute a part of a mathematical equation with its partner! Consider this question:
"Given f(x) = 2x2 + 1 and g(x) = x - 1, find fg(3)."
Complicated, is it? You don't know the 'instructions' for Function fg(x)... however, fg(3) is another way of writing f(g(3)). Ok, you know that g(3) = 2. Aha! You can substitute "g(3)" with "2", giving you... f(2). Now we're getting somewhere!
| f(2) | = 2(2)2 + 1 |
| = 2(4) + 1 = 9 |
Therefore, fg(3) = 9
Similarly, using g(x) = x - 1 and f(3) = 19 to solve gf(3):
| gf(3) | = g[f(3)] |
| = g(19) = (19) - 1 = 18 |
Note carefully that fg(x) is NOT gf(x).
Alright, moving on! Working out f(x) or g(x) individually before combining with fg(x) or gf(x) is a perfectly correct way of doing it. However, you might want to work out the 'instructions' for the compound functions themselves.
To do that, you must remember 2 things:
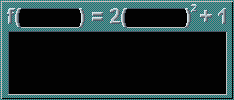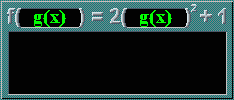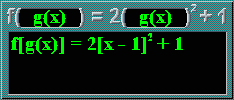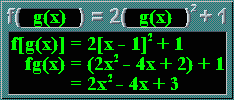

The green 'flashes' in the machines represent replacement of a section. However, they didn't quite look as good as I intended, hehe... No worries, here's a recap, with f(x) = 2x2 + 1 and g(x) = x - 1:
| fg(x) | = f[g(x)] |
| = f(x - 1) = 2(x - 1)2 + 1 = 2(x2 - 2x + 1) + 1 = (2x2 - 4x + 2) + 1 = 2x2 - 4x + 3 |
|
| gf(x) | = g[f(x)] |
| = g(2x2 + 1) = (2x2 + 1) - 1 = 2x2 |
So, fg(x) = 2x2 - 4x + 3 and gf(x) = 2x2. Use your new equations to find fg(3) and gf(3). You will see that the answers match those at the top of the page.
Since you can combine 2 different functions, you can also combine a function with itself!
| f[f(x)] | = f(2x2 + 1) |
| = 2(2x2
+ 1)2 + 1 = 2(4x4 + 4x2 + 1) + 1 = (8x4 - 8x2 + 2) + 1 = 8x4 + 8x2 + 3 |
|
| g[g(x)] | = g(x - 1) |
| = (x - 1)
- 1 = x - 2 |
A self-combining function is written as f2(x). Be careful, do not confuse this with a square (kuasa dua)! While g2(x) = x - 2, [g(x)]2 = [x - 1]2 = x2 - 2x + 1
You can also keep adding on more functions: f3(x) = f( f( f(x) ) ), f4(x) = f( f( f( f(x) ) ) ) and so on.
Similarly, you can have a chain of different functions, like fgh(x). In this case, you have to work 'inside out': Find gh(x) 1st, then put it into f(x).
Page: 1 | 2
The Notes
Portal Home