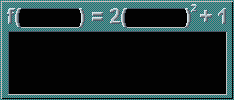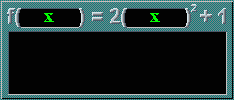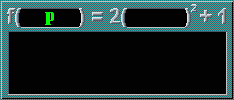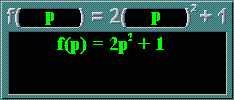
FUNCTIONS
I. How They Function
A function is more or less another algebraic equation, like y = 6x - 1
or 3a - 2 = 5b, only with a few distinct methods of writing. In analogy,
a function can be seen as a molding machine. When you put a number into it, the
number is shaped (transformed) into something else.
Here's an example:
f(x) = 2x2 + 1
The left side of the equation tells you the function's name (in this case, the name is 'f'. 'f' is the most common name, but any other letter can be used.), and what it's transforming (in this case, it is transforming x). The right side of the equation tells you how the transforming is done.
Here, the left side tells us that Function f is working on x. The instructions on the right side says:
i) Take x and square it
ii) Multiply it by 2
iii) Add 1
People are often confused by the different x's in the equation. Actually, the function can be seen like this:
f(.....) = 2.....2 + 1
The blank sections are 'waiting' for a number to be put inside them. It's just that in writing, you can't leave black spaces in equations, so an x is put there to to 'stand in' until a number comes along. Sometimes, other letters can be used too. The following all say the same thing:
f(x) = 2x2 + 1
f(y) = 2y2 + 1
f(p) = 2p2 + 1
f(q) = 2q2 + 1
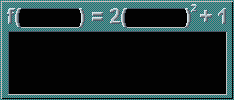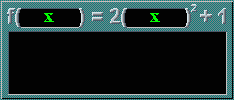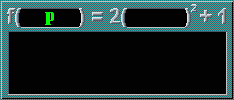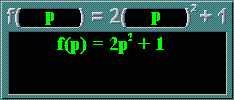
In the 'machine' above, only the spaces can be changed. Notice that all the other numbers are 'fixed'. Remember, when the spaces are filled, the same number (or unknown ['anu'], or expression ['sebutan']) must be placed in ALL the spaces.
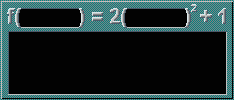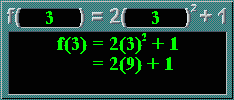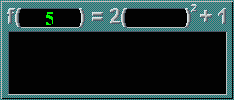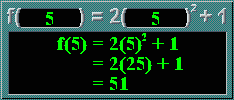
So far, you have only dealt with simple, straightforward functions. However, these concepts are important when dealing with more complicated ones in later sections.
Page: 1 | 2
The Notes
Portal Home