Creazione di funzione hash

per archivi statici: possibili miglioramenti

 

Si può dimostrare che dato un qualche insieme di chiavi, tutte distinte e conosciute, si può costruire una funzione hash minima e perfetta. Tuttavia l’algoritmo che si ottiene dalla dimostrazione ha una complessità in tempo esponenziale e quindi non può essere usato in modo conveniente per un numero di chiavi abbastanza elevato. Si è quindi cercato di ottenere algoritmi con complessità minore, in particolare con complessità polinomiale. L’algoritmo illustrato in seguito ha una complessità lineare in tempo e spazio, se il numero delle chiavi è infinito: ovvero la probabilità di ottenere una funzione hash perfetta e minima tende ad 1 al crescere del numero delle chiavi e analogamente la complessità tende ad allinearsi con quella lineare. Quindi non ci dovrà preoccupare una complessità non esattamente lineare per un numero basso di chiavi.

L’algoritmo proposto cerca a caso una funzione hash opportuna dopo aver diviso le chiavi in gruppi più piccoli: anche questa divisione avviene in modo casuale. È importante per il corretto funzionamento dell’algoritmo che i numeri casuali siano davvero tali, o almeno un’ottima approssimazione, e per questo mi sono preoccupato di costruire un generatore di numeri casuale e di testarlo per verificarne l’attendibilità. Inoltre sono necessarie al funzionamento dell’algoritmo un numero di chiavi, nel nostro caso, parole, sufficientemente alto, ma tutte distinte. Perciò ho approntato un programma per generare un certo numero di parole, di dimensioni variabili, tutte differenti, in modo da simulare un vero dizionario.

Infatti un interessante uso per questo algoritmo è quello di creare un efficiente sistema di ricerca in database molto grandi e statici. Infatti una volta trovata la funzione hash si può ricercare una chiave in questo database in tempo nullo. Il tempo per calcolare la funzione hash sappiamo essere un tempo umanamente accettabile per la complessità lineare tendenziale dell’algoritmo. È inoltre opportuno ricordare che il calcolo della funzione hash va fatto una sola volta e quindi non è negativo che il tempo di creazione di questa sia elevato, anche perché la complessità lineare ci garantisce la non esplosione di questi tempi.

II. Idee generali

L’idea generale su cui si basa l’algoritmo è quella di dividere le chiavi in tanti piccoli gruppi con le seguenti caratteristiche:

Le chiavi devono essere distribuite in modo uniforme in questi gruppi, e quindi ognuno deve contenerne il minor numero possibile

Non deve esserci alcuna relazione tra le chiavi contenute in ciascun gruppo: in altre parole la suddivisione deve essere quanto più casuale possibile.

È ovviamente impossibile ottenere le due caratteristiche al meglio e una parte del programma cerca appunto di risolvere questo problema: in particolare si ottimizza il primo punto rispetto al secondo, cioè si cerca di ottenere gruppi il più possibile uniformi di chiavi scelte casualmente. Una volta che abbiamo ottenuto questi gruppi applichiamo la seguente funzione hash:

Espressione -1- Funzione Hash 1

Ove "key" è la chiave, h0 e h2 sono due funzioni opportune, mentre "i" indica il gruppo di cui "key" fa parte. L’ultimo passo dell’algoritmo è appunto dedicato alla ricerca di tale funzione g(.) in modo che tutte le h(key) risultino distinte. Si può dimostrare che con delle opportune h0 e h2, la ricerca di tale funzione g ha sempre successo in un tempo che cresce linearmente con il numero delle chiavi se questo numero è molto grande. Grande importanza per l’algoritmo riveste come si può capire fin d’ora il poter disporre di numeri realmente casuali. Questo non è possibile e poiché i normali generatori di numeri casuali hanno un range molto limitato ho preferito utilizzare un diverso generatore di numeri casuali, secondo il metodo della congruenza lineare che poi ho testato.

Tutti i programmi sono stati scritti in C++ ad oggetti. Questa scelta è stata fatta perché nel procedere con il programma si devono creare delle strutture che poi possono essere facilmente riutilizzate in altri programmi. Per cercare di superare il limite dei 640 KB imposti dal sistema operativo DOS ho compilato i programmi per Windows a 16 bit, per poter sfruttare la compilazione EasyWindows che permette di aggirare la gestione dell’interfaccia e si vede come un programma DOS.

III. Generatori di numeri casuali

Il metodo seguito è quello di D. Lehmer, detto della congruenza lineare. La sua implementazione non richiede particolari difficoltà tranne alcuni semplici accorgimenti che illustro.

Algoritmo -1 - Definizione dell’oggetto TRandom

Questo è l’oggetto che genera numeri casuali. Nella parte riservata ci sono le variabili "a", "m" e "b" necessarie per l’algoritmo. È inoltre presente una variabile m1 di appoggio perché, essendo necessario eseguire moltiplicazioni tra numeri molto grandi di cui si deve poi fare il modulo, è probabile che durante la moltiplicazione si verifichi un overflow. A ciò si rimedia con un’apposita funzione mult() che accetta in ingresso due interi p e q, per restituire (p*q)%m. Per questo deve essere m1^2 = m.

Il costruttore Trandom provvede ad inizializzare tutte le variabile ed a porre "a" pari al valore passato come argomento, il seme della sequenza casuale. In seguito si è posto anche il problema di come trovare un seme sempre diverso, in modo da ottenere numeri casuali differenti.

La funzione succ richiede come argomento un range e restituisce un numero casuale opportuno, calcolato secondo il noto algoritmo:

Algoritmo -2 - Calcolo del numero pseud. casuale successivo 1

Con quest’oggetto poss ottenere numeri casuali tra 0 e 2^32-1.

Ho eseguito quattro gruppi di prove, generando rispettivamente numeri fino a 100, 1000, 10000, 20000 per verificare l’efficienza del sistema proposto in confronto con la funzione random del C, per la quale sono state svolte le medesime prove.

Ci si è avvalsi della formula

Espressione -1 - Test 1 di casualità

Dove Nprove è il numero di numeri casuali generati; Range è il range e Freq(i) rappresenta la frequenza con cui ogni numero da 0 a Range è stato generato durante le Nprove. Ovviamente Nprove >> range (per la precisione si è fissato il rapporto Nprove/range pari a 100).

Notiamo che se le frequenze sono tutte uguali, pari a Nprove/range, test è uguale a 0. Quindi un numero pari a 0 indica numeri molto casuali, mentre un numero molto lontano indica che ci sono delle preferenze. Eseguendo i test si ottengono i seguenti risultati

Figura -1 Test Casualità

A questo grafico è associata la Tabella 1 (*) per vedere i numeri esatti. Come si vede bene dal grafico il generatore standard del C (tratteggiato) tende a non funzionare bene per Range alti, mentre quello implementato, secondo il modello di Lehmer funziona sempre con la stessa regolarità. Questo pregio lo paghiamo in velocità: non utilizzando routine assembler questo sistema è circa 10 volte più lento.

Ho avuto modo di notare che anche il generatore nuovo tende ad esplodere per range elevati, ma questo è probabilmente dovuto ad un problema di overflow nel calcolo del numero casuale nella funzione succ. Per evitare questo si può sostituire Algoritmo III-2 sopra definito con la seguente:

Algoritmo -3 - Calcolo del numero pseud. casuale successivo 2

long double TRandom::succ(void)

{

a = (mult(a, b) + 1) % m;

return (((long double)a)/m);

}

che genera un numero tra 0 e 1 estremamente preciso. Sarà poi sufficiente moltiplicarlo per il Range per ottenere il risultato voluto. I dati del grafico di sopra sono stati ottenuti con questa nuova funzione.

IV. Dizionario

Abbiamo detto che per costruire una hash perfetta e minima dobbiamo conoscere in anticipo tutte le chiavi e queste devono essere, ovviamente, tutte distinte. Per testare l’algoritmo servono molte parole differenti e non disponendo di un vero dizionario ho ideato un programma per generare un dizionario casuale con queste caratteristiche:

possa generare almeno un centomila parole;

generi parole tutte differenti tra di loro;

queste parole siano di dimensione variabile.

Quindi ho pensato di utilizzare il seguente schema:

<I1I2I3>[(I3)(I3+1)...(I3+18)]

Cioè ogni parola è composta da un gruppo di tre lettere a cui si aggiungono altre lettere (da 0 a 18) che sono la lettera dopo i3, la lettera dopo ancora, e così via. Per le prime tre lettere si effettuano delle permutazioni. Così si ottiene, per esempio:

aaa aaaa aaaab aaaabc ...

aab aabb aabbc aabbcd...

aaz aazz aazza aazzab..

...

Si ottengono così 26^3*19 > 300000 parole. Queste poi sono tutte differenti perché, a parità delle prime tre lettere che sono tutte differenti, cambia la lunghezza. Inoltre vengono coinvolte velocemente tutte le lettere dell’alfabeto. Come alfabeto semplicemente quello inglese, ma non c’è nessuna difficoltà a considerare anche numeri o altri simboli.

Per ottenere i risultati di cui sopra è stato creato un apposito oggetto chiamato TParolaCasuale.

Algoritmo -1 - Definizione dell’oggetto per creare un dizionario casuale

Le variabili id e par contengono le due parti della parola; max contiene il numero massimo delle parole, att la parola che viene generata in quel momento. Le due funzioni riservate Forma e Calcola rispettivamente formano e calcolano la seconda e la prima parte della parola, basandosi sulla precedente. Vengono chiamate dal costruttore e dai due operatori.

Il costruttore viene chiamato senza argomenti e inizializza le variabili e forma la prima parola. Leggi() restituisce la parola attuale, mentre per spostarsi alla parola successiva o tornare alla precedente è sufficiente usare gli operatori ++ e -- in forma postfissa che sono stati ridefiniti. Per esempio

Algoritmo -2 - Esempio di uso di TParolaCasuale

TParolaCasuale miapar();

char buf[30];

strcpy(buf, miapar.Leggi()); miapar++;

Ovviamente non è stato implementato un metodo per accedere ad una parola qualunque perché oltre ad essere inutile è dispendioso in tempo in quanto le permutazioni sono un tipico problema esponenziale non riducibile. Per scrivere su disco le varie parole man mano create si è fatto uso degli stream predisposti nelle librerie del C++. Le possibilità che si superi il numero massimo di parole consentito o si scenda sotto il valore zero sono gestite all’interno degli operatori ++ e -- che in tali casi restituiscono 0 e gestiscono l’errore, altrimenti restituiscono 1.

Non ci sono problemi di complessità che per generare una nuova parola è dell’ordine di O(1) e anche lo spazio occupato è insignificante.

V. Funzione Hash

Abbiamo detto che la gran parte dell’algoritmo serve per definire la funzione g(i) presente all’interno di h(key). Tuttavia sono lì presenti altre due funzioni h0 e h2 e indirettamente anche una terza funzione h1. L’algoritmo si suddivide in tre parti delle quali la prima serve per definire queste funzioni.

Mapping. Questo passo crea anzitutto tre tabelle di dimensione MAXCAR x MAXLUNG di numeri casuali. MAXCAR rappresenta la cardinalità dell’alfabeto considerato, nel nostro caso 26. MAXLUNG rappresenta la massima lunghezza delle parole, nel nostro caso 22. È necessario conoscere questi valori in anticipo per poterli comunicare al programma. A questo punto definiamo

Espressione -1 - Funzioni h0, h1, h2

dove % indica l’operazione modulo e la k vale il numero delle parole se i = 0 e 2, mentre vale r nel caso i = 1. "r" è un valore definito in modo opportuno all’aumentare del quale diminuisce la memoria occupata ed aumenta il tempo di calcolo. Il valore minimo per r è dato da: dove c in genere vale 4. Qualora n sia troppo piccolo questa espressione assume valori troppo grandi e se supera la metà del numero delle parole si prende r uguale a quest’ultimo valore.

Ordering. Questo passo si occupa formare i citati gruppetti, uniformi e casuali: questo è molto semplice in quanto questi gruppetti corrispondo a quelli che hanno la medesima h1. Si verranno perciò a creare r insiemi di cardinalità varia o anche vuoti, detti in seguito K-Liste. Si stabilisce inoltre l’ordine con cui tali gruppetti dovranno essere trattati nel passo successivo nel seguente modo: prima quelli di cardinalità maggiore, a parità di questa quelli con h1 più piccola.

Searching. Come dice il nome questo passo cerca il valore per la funzione g. Procede nel seguente modo. Considera il primo gruppetto del passo 2 e assegna un valore casuale di g per quel gruppetto e calcola la funzione h(key) per tutte le chiavi del gruppetto. Se vengono assegnate a posizioni vuote le alloca, altrimenti cerca un nuovo valore di g. Poiché il valore della funzione g deve essere compreso tra 0 e numero delle parole anziché un generatore di numeri casuali si considera il resto nelle divisioni con un qualche numero primo e con i suoi multipli. Quindi si prova con il secondo gruppo, dove l’ordine è stato stabilito nel passo 2, e così via. Se l’allocazione di un gruppetto non riesce alla prima (cosa probabile) si effettua un backtracking o all’interno dello stesso passo o se è necessario dal passo 1, ricalcolando le tabelle e la suddivisione in gruppetti.

Per costruire la mia tabella Hash ho creato una libreria di oggetti standard. Questa contiene oltre al già citato generato di numeri casuali una struttura per gestire vettori dinamici di interi positivi.

Algoritmo -1 - Oggetto Vettore dinamico di interi positivi

class TVettoreDin

{

private:

unsigned dim; ulong* p;

 

public:

TVettoreDin(unsigned ddim) { ... }

~TVettoreDin(void) {...}

void Init(ulong a = 0);

void scrivi(unsigned x, ulong cosa) { ...}

ulong operator[](unsigned x) { ...}

friend ostream& operator << (ostream& s, TVettoreDin* q);

};

Il costruttore richiede la dimensione. Per leggerlo è sufficiente utilizzare il solito operatore [] opportunamente sovrascritto, analogamente per l’output si può usare l’operatore <<. Per scrivere si deve chiamare la funzioni scrivi con argomenti la posizione ed il valore da scrivere. Init() azzera il vettore e viene sempre chiamata dal costruttore.

Algoritmo -2 - Oggetto Tabella dinamica di interi positivi

class TTab

{

protected:

unsigned x, y;

ulong** p;

public:

TTab(unsigned dx, unsigned dy);

TTab(char*);

TTab(istream *f) {... }

~TTab (void);

virtual void Init(void);

void scrivi(unsigned x, unsigned y, ulong cosa) { ... }

ulong* operator[] (unsigned dx) {...}

friend ostream& operator<< (ostream& s, TTab* q);

friend istream& operator>> (istream& s, TTab* q);

virtual void Salva(char*);

virtual void Salva(ofstream *f) { ... }

};

I costruttori sono di tre tipi: il primo richiede le due dimensioni e prepara una tabella vuota; il secondo chiede il nome di un file da cui caricarla; il terzo chiede uno stream da cui caricarla. Questo stream può derivare dal nome di un file. Per la scrittura di un valore viene definita la funzioni scrivi, analogamente per la lettura viene ridefinito l’operatore []. Vengono ridefiniti gli operatori << e >> per l’ingresso e l’uscita dell’intera tabella; la funzione Salva trasmette la tabella ad un file o ad uno stream a seconda di come viene chiamata.

Algoritmo -3 - Oggetto Tabella dinamica di interi positivi random

class TTabRand : public TTab

{

private:

ulong max;

PTRandom rand;

unsigned userandom;

 

public:

TTabRand(unsigned dx, unsigned dy, unsigned m) : TTab(dx, dy)

{ ... }

TTabRand(unsigned dx, unsigned dy, ulong m, PTRandom r) : TTab(dx,dy) {... }

TTabRand(ifstream *f) : TTab(f) {};

TTabRand(char* nome) : TTab(nome) {};

void Init(void);

};

Derivata da TTab. I costruttori qui sono quattro: due caricano la tabella da stream o da file e si limitano a chiamare il costruttore in TTab; il primo chiede la dimensione x, y ed un valore massimo che non può superare 65535: la tabella viene costruita utilizzando la funzione random del C; il terzo costruttore oltre agli argomenti precedenti un puntatore all’oggetto Generatori numeri casuali e questa volta la tabella viene inizializzata utilizzando questo generatore ed la variabile m può valere fino a 4 miliardi circa. Se non servono numeri molto grandi è più veloce chiamare il costruttore 1. La funzione Init viene ridefinita. Anziché azzerare la tabella, assegna nuovi valori casuali.

Algoritmo -4 - Oggetto Vettore dinamico di stringhe di lunghezza variabile.

class TVetString

{

protected:

unsigned dim;

char** p;

 

public:

TVetString(char*, unsigned);

TVetString(unsigned, ...);

~TVetString(void);

char* operator[] (unsigned dx) {...}

friend ostream& operator <<(ostream& s, TVetString q);

};

Il costruttore 1 carica le stringhe da un file e richiede come secondo argomento il numero di stringhe da caricare. Per ogni stringa viene allocata la memoria strettamente necessaria. Il costruttore 2 chiede anzitutto il numero delle stringhe che poi devono essere scritte una di seguito all’altra separate da una virgola. Vengono ridefiniti gli operatori [] e << per la lettura rispettivamente di una e di tutte le stringhe. Questo oggetto funziona solo in lettura.

La creazione di queste strutture è il minimo necessario per il funzionamento dell’algoritmo senza decidere a priori il numero delle chiavi. Sono state tolte tutte le implementazioni che si trovano nell’allegato, quelle inline sono state tutte sostituite da { ... }.

Anche la tabella Hash è un oggetto

Algoritmo -5 - Oggetto Tabella hash

class THash : public TVetString

{

private:

PTRandom rand;

PTTabRand tab0, tab1, tab2;

PTVettoreDin h0, h1, h2;

PTVettoreDin cardin;

PTVettoreDin* Kliste;

PTVettoreDin assegnati;

PTVettoreDin Gvalori;

PTVettoreDin Mark;

unsigned* ordins;

PTVettoreDin Hash;

 

unsigned maxcard;

unsigned r;

unsigned primo;

unsigned cardmag1;

 

void Init(unsigned);

void Creah1(void);

void CreaKliste();

void verifica(void);

void AssegnaKLista(unsigned, unsigned, unsigned *ok);

int CreaHash(void);

void CercaHash(void);

public:

THash(unsigned c, char *nome, unsigned ddim) : TVetString(nome, ddim) { ... }

~THash();

};

 

Come si vede THash deriva dal vettore di stringhe dinamico perché alla fine è solo un particolare tipo di vettore di stringhe dinamico. Come si vede dalla dichiarazioni delle variabili vengono utilizzate tutte le strutture del precedente paragrafo. Il funzionamento dei punti cruciali verrà illustrato in seguito. Qui mi limito ad esporre il funzionamento. Disponendo di quest’oggetto e di un file con le stringhe è sufficiente scrivere:

Algoritmo -6 - Utilizzo dell’oggetto THash

void main ()

{

THash* h;

h = new THash(c, nomefile, numkey);

delete h;

}

per creare la Tabella Hash. ‘c’ è un valore che deve essere scelto opportunamente in base a numkey ed alla memoria disponibile, generalmente si sceglie 4. È inutile allocare staticamente la tabelle Hash in quando una volta chiamato il costruttore e creata la tabella la struttura diviene inutile. Questa istruzione chiama il costruttore e questo procede costruendo la tabella Hash e salvando le tre tabelle; il vettore Gvalori e il vettore Mark. Il meccanismo con cui la tabella Hash viene creata è il seguente:

Il costruttore THash chiama il costruttore di TVetString e carica le stringhe in memoria; quindi chiama Init().

Init alloca tutte le strutture dinamiche di cui adesso è nota la dimensione, tranne le KListe di cui ancora non si conosce la dimensione; quindi chiama verifica()

Verifica chiama Creah1() che calcola i valori per h0, h1, h2 dalla tre tabelle e dalle chiavi; calcola inoltre il vettore delle cardinalità in base ai valori di h1 e trova il valore massimo tra queste cardinalità. Chiama CreaKListe()

Alloca le KListe e gli assegna i valori opportuni. Viene determinato e memorizzato l’ordine con cui le KListe dovranno essere allocate nella tabella Hash. A questo punto Klista per Klista, ovvero a parità di h1, si verifica se non ci sono triple uguali. Se ci sono le KListe vengono deallocate e si torna al punto 3, altrimenti si procede.

Si esce da verifica() e si torna ad Init(). Quest’ultima chiama CercaHash()

Viene chiamata CreaHash() la quale cerca di collocare nella tabella tutte le Kliste una per una chiamando AssegnaKLista(...). CreaHash() procede finché AssegnaKLista(...) non restituisce un valore zero. In tal caso anche CreaHash si chiude restituendo il valore del massimo gruppo allocato. Se tutte le KListe vengono assegnate CreaHash restituisce zero.

Se in ritorno da CreaHash non c’è zero questa viene richiamata di nuovo con diverse condizioni. Dopo un numero elevato di chiamate a CreaHash viene rifatto tutto dal punto 3. Quando CreaHash restituisce 0 si passa avanti

Vengono salvate le tabelle e i tre vettore e si esce da Init(). Quindi si esce anche dal costruttore.

Ai fini dei test ho considerato

MAPPING il punto 2.

ORDERING il punto 3 e 4

SEARCHING i punti 6 e 7

Con n, numkey, dim si intende sempre e solo il numero delle chiavi. Con r in tutto il programma si farà riferimento al valore di r sopra definito.

Questo passo è abbastanza semplice. Le tre tabelle vengono create utilizzando l’oggetto TTabRand, derivato da TTab. Inoltre viene calcolata r come sopra definita. Per il calcolo del logaritmo di 2 non ho usato le funzioni standard, ma ho contato il numero di shift a destra necessari per azzerare dim. Infine vengono allocati tutti i vari vettori dinamici.

Algoritmo -7 - Calcolo di r

Algoritmo -8 - Allocazione e calcolo delle tabelle Random

tab2 = new TTabRand(MAXCAR, MAXLUNG);

I tempi necessari per questo non bassi e crescono sub linearmente con la dim. In realtà le tabelle sono tutte uguali, ma forse incide il fatto che si debbano utilizzare puntatori lunghi con dim molto alta.

Figura -1 - Tempi per l’allocazione dei dati e la creazione delle tabelle (ms)

Ricordo che ogni funzione polinomiale si presenta lineare in un grafico con scala logaritmica che sono costretto ad usare per leggibilità: per valutare la linearità è necessario vedere qual è la funzione esponenziale "interpolante" e ricavare quindi il grado del polinomio. Se per esempio la funzione esponenziale è 10*exp(0.69x) allora l’andamento è circa lineare: infatti exp(0.69) = 2 e lungo le ascisse la scala raddoppia ad ogni segno. Se 10*exp(1.79x) è cubica perché exp(1.79) = 6 e 6/ 2 = 3 se la scala delle ascisse segue un andamento tipo k*2^x

Nel caso specifico abbiamo una sub-linearità, in quanto il grado ottenuto è leggermente superiore ad 0 (grado = 0.16), come d’altra parte ci si aspettava in quanto questa parte è abbastanza indipendente da numkey.

Questi tempi quindi, già trascurabili con 16000 chiavi, resteranno tali anche per qualche milione di chiavi. I tempi per il calcolo di h0, h1, h2 sono inclusi nei tempi successivi.

Questo passo si occupa solo di dividere nei vari gruppetti le chiavi. A tal proposito si utilizza un vettore di puntatori a TVettoriDin, chiamato Kliste. Ci sono r puntatori a TVettoreDin, uno per ciascun valore di h1 e ogni TVettoreDin ha una dimensione pari alla cardinalità per quel valore di h1. In pratica KListe[i] punta al vettore che conterrà tutte le chiavi con h1(key) = i e KListe[i][0] ... KListe[i][cardin(h1)] contengono tutti i valori del numero della chiave con h1(key) = i.

Algoritmo -9- Allocazione in memoria delle KListe

Kliste[i] = new TVettoreDin((unsigned)(*cardin)[i]);

7Queste righe allocano KListe. Il vettore dinamico pos viene posto a 0 dal costruttore e serve nella carte successiva per sapere in quale posizione poter memorizzare la chiave. La memorizzazione delle chiavi avviene nel semplice ciclo:

Algoritmo -10 - Creazione delle KListe

Complessità di scrittura dovuta ai puntatori il seguente ciclo si comporta nel modo seguente:

Memorizza il numero della chiave i-esima (quindi il valore i) in KListe[h1(key)][a]. Qual è "a"? Questo valore è scritto in Pos[h1(key)] e all’inizio è zero, poi mano a mano che si inseriscono chiavi con medesimo h1 si incrementa Pos.

Incrementa di uno Pos[h1(key)] in modo da memorizzare la successiva chiave con medesimo h1 nella posizione successiva.

Quindi sostanzialmente un ciclo for: difatti non c’è possibilità di errore nella creazione delle KListe.

Algoritmo -11 - Calcolo dell’ordine di inserimento

nt = 0;

for (i = maxcard; i > 1; i--) for (j = 0; j < r; j++)

if ((*cardin)[j] == i) ordins[nt++] = j+1;

 

Questi due cicli nidificati calcolano l’ordine con cui le K-Liste dovranno essere inserite nella tabella hash, ovvero da quella con cardinalità maggiore fino a quelle con cardinalità 2. Pur essendo due cicli uno interno all’altro la complessità resta lineare. Infatti maxcard cresce come O(log(n)), mentre r è per definizione O(n/log(n)). Dunque la complessità del ciclo è proprio O(n). Nel caso in cui r sia n/2 la complessità di questo ciclo sale a O(n*logn).

Più difficile l’analisi del ciclo successivo che si preoccupa di verificare che le triple siano distinte. Per migliorare la complessità si effettuano solo confronti all’interno di ciascuna K-Lista con almeno due elementi, dove già sappiamo essere uguale il valore di h1.

Algoritmo -12 - Verifica della non coincidenza delle triple h0,h1,h2

for (k = 0; k < cardmag1 && !l ; k++)

{

nkl = ordins[k] - 1;

c = (unsigned)(*cardin)[nkl];

for (i = 0; i < c && !l; i++)

for (j = i+1; j < c && !l; j++)

{

nk1 = (unsigned)(*(Kliste[nkl]))[i];

nk2 = (unsigned)(*(Kliste[nkl]))[j];

if ((*h0)[nk1] == (*h0)[nk2] &&

(*h2)[nk1] == (*h2)[nk2])

{

tab0->Init(); tab1->Init(); tab2->Init();

cardin->Init();

for (l = 0; l < r; l++) delete (Kliste[l]);

delete[] Kliste;

for (l = 0; l < r; l++) ordins[l] = 0;

l = 1;

collisioni++;

}

}

}

Essendoci tre cicli nidificati la complessità asintotica è data dal prodotto di cardmag1*c*c; il primo è dell’ordine di O(n/log(n)) in quanto dipende direttamente da r e nel caso migliore vale esattamente r; c come sopra è dell’ordine di O(log(n)) e nel caso migliore tutti i valori di c sono uguali pari esattamente ad log(n). Quindi il limite inferiore della complessità è O(n*log(n)). Nel caso peggiore cardmag1 vale esattamente 1, mentre c vale n ed è il caso in cui tutti i valori di h1 sono uguali. In questa situazione del tutto improbabile per l’efficienza dei generatori di numeri casuali proposti la complessità è proporzionale a n^2, ma questo caso oltre ad essere improbabile è anche inaccettabile per il funzionamento del programma: il suo verificarsi dovrebbe far rivedere tutto.

Figura -2 - Tempi per il calcolo di h1 e di verifica triple distinte(ms) nel caso di r minimo

Il grado ottenuto è leggermente inferiore ad 1, 0,97 per la precisione. Come si vede le previsione teoriche vengono rispettate e si evidenzia una linearità netta. Nel caso r = n/2, previsto non lineare non si riescono comunque a notare scostamenti dalla linearità (grado = 0.97 nuovamente), anche se i tempi risultano tutti più alti (vedi Tabella 2 *).

Questo passo si occupa di allocare nella tabella Hash le K-Liste. Si compone di tre funzioni:

AssegnaKLista cerca di allocare una ben precisa K-Lista, ovvero tutte le sue chiavi. Questa funzione può non riuscire se il valore Hash di una chiave, al variare di tutti i possibili valori di g, coincide con una posizione precedentemente assegnata. È quindi importante che la funzione Hash, fissati h0 e h2 generi il maggior numero di posizioni differenti al variare di g.

CreaHash cerca di allocare tutte le chiavi chiamando AssegnaKLista. In un primo tempo si era costruito all’interno di questa funzione un meccanismo di backtracking che forse può avvantaggiare per valori di n molto alti e solo quando quasi tutte le K-Liste sono state assegnate. Nella versione proposta non appena una Klista non viene allocata CreaHash si interrompe comunicando il fallimento.

CercaHash chiama CreaHash finché la tabella hash non viene creata. Nel caso, frequente, che non riesca opera due forme di backtracking che fanno in ogni caso ripartire CreaHash dalla prima K-Lista. Nel primo caso, detto semplicemente backtracking, si limita a richiamare CreaHash variando il valore di g iniziale e molto probabilmente tutti i valori seguenti; nel secondo, detto ricalcolo, vengono calcolate di nuovo le tabelle e quindi rifatte le K-Liste.

L’efficienza di questo passo dipende sostanzialmente dalla funzione Hash che deve avere la caratteristica di essere un buon generatore di numeri casuali ed anche di generare molte posizioni differenti al variare di g. Non si può fare una semplice analisi della complessità di questi algoritmi, in quanto sono nettamente probabilistici. Mi limiterò a trarre delle conclusioni dai test effettuati.

Riscontrando problemi nella ricerca della funzione Hash, ovvero dei valori della funzione g(i), i = 0, ..., r ho pensato di testare il comportamento casuale della funzione proposta e anche di una mia funzione Hash, sempre quadratica data dalla seguente:

Espressione -2 - Funzione Hash 2

Poiché riscontravo valori del tutto non accettabili con il test di casualità precedente l’ho sostituito in questa nuova serie di test con il seguente.

Espressione -3 - Test di casualità 2

Anche questo test come il precedente tende a zero se la distribuzione è uniforme, tuttavia ha una precisione molto maggiore. Durante i test eseguiti è stato fatto assumere a g tutti i valori possibili, h0 e h2 sono stati calcolati attraverso il generatore di numeri casuali, in quanto l’effetto che si ottiene con la funzione h0 e h2 è esattamente quello. Sono stati fatti test al variare del numero delle chiavi, mantenendo r fisso pari alla metà del numero delle chiavi. Poi con due numeri di chiavi particolare sono stati fatti test al variare di r, in quanto come vedremo è soprattutto questo numero ad influenzare i risultati. Riportiamo il primo grafico con i valori del test, al crescere del numero delle chiavi per il generatore di numeri casuali utilizzato; la funzione Hash proposta dall’algoritmo (Hash 1) e dalla funzione Hash di cui sopra (Hash 2).

Figura -3 - Casualità delle funzioni Hash

 

Come si vede dal grafico, in scala logaritmica su ambedue gli assi, soltanto la funzione Hash 2 segue l’andamento del generatore di numeri casuali, mentre la prima se ne discosta molto per valori inferiori a 4000. Peraltro proprio per quel valore cambia l’andamento della curva, prima fortemente lineare. Questo indica un difetto del generatore di numeri casuali che tuttavia ritroviamo anche con il generatore del C. Per valori elevati il generatore random tende a scendere verso lo zero e così anche le due funzioni Hash, d’altra parte sono esse stesse generatori random, e la prima segue il generatore random meglio della seconda. Sembra infine che la prima sia leggermente migliore della seconda per valori alti, ma del tutto insoddisfacente per un numero di chiavi bassi. I valori ottenuti da questo grafico sono riassunti nella  

Tabella 9

.

Detto questo l’algoritmo di Searching non funziona con nessuna delle due: in particolare riusciamo ad ottenere un qualche risultato con la Hash 1, ma non si riesce ad ottenere alcun risultato ragionevole con la Hash 2. A questo punto mi sono chiesto quale deve essere la caratteristica non tanto di una generica funzione Hash, ma della funzione Hash per il mio algoritmo. Si nota che il comportamento casuale è necessario a garantire una elevata velocità, ma non sufficiente: difatti se non riesce subito l’allocazione variando g è utile che vari anche la funzione hash. Ho perciò definito due indici per misurare ciò:

Valori differenti complessivi (VDC): dato dal numero di valori differenti per la funzione hash generati da differenti valori di g.

Valori differenti utili (VDU): dato dal rapporto tra il numero di volte che la funzione hash è riuscita a generare al variare di g almeno la metà dei valori possibili e il numero di prove totali.

Espressione -4 - Test VDU

Freq(i) contiene il numero di volte che nelle numerose prove sono state generati i posizioni differenti.

Il primo indica la possibilità che vengano generate tutte le posizioni in un ciclo al variare di g; il secondo è come il primo, ma vengono escluse tutte le frequenze più piccole ed è quindi un indice più severo, ma più indicativo. Vale generalmente:

Esistono funzioni hash in grado di raggiungere il valore massimo, come la seguente:

Espressione -5 - Funzione Hash 4

Si vede bene che se fissiamo h0 ed h2 al variare di g tra 0 e quanti otteniamo, per definizione di modulo, tutti i valori tra 0 e quanti. Quindi in tal caso VDU = VDC = 1. Chiameremo questa funzione Hash 4. Definiamo inoltre una funzione Hash 3:

Espressione -6 - Funzione Hash 3

Sia la Hash 3 sia la Hash 4 ha un comportamento nel test di casualità come la Hash 2. Tuttavia per la Hash 4 troviamo che non è un buon generatore di numeri casuali perché il suo periodo, a parità di h0 e h2, è numkey. Inoltre la Hash 1 e la Hash 2 non hanno dei buoni valori di VDC e VDU, anzi il secondo che è il più importante è molto, troppo, basso. A scopo di esemplificazione un VDU pari a 0,18 significa che c’è solo il 18% di probabilità che al variare di g da 0 a numkey la funzione Hash assuma più di numkey/2 valori differenti o anche che generalmente vengono generati numkey/10 valori differenti. Questi valori sono casuali, con h0 e h2 differenti, tuttavia quando la tabella è già molto piena è molto utile che la funzione hash sia in grado di scandirla quasi tutta e comunque maggiore è il numero di posizioni differenti rintracciate dalla funzione Hash, maggiore è la possibilità che il gruppetto venga allocato. Allora la soluzione migliore sembrerebbe la Hash 4, ma non è così: questa infatti scandisce tutta la tabella, ma è poco casuale e quando deve allocare due chiavi e quindi se è sempre in grado di trovare un valore buono per la prima chiave, la scarsa casualità "impedisce" che tale valore di g sia buono anche per la seconda chiave. In parole povere la Hash 4 è molto buona quando teniamo fermi h0 ed h2 e facciamo variare g, ma non altrettanto quando g è fissa e variano h0 ed h2. Riepilogando:

la Hash 1 (2) al variare di h0 ed h2 con g fissa produce pochi numeri differenti e produce molti numeri differenti con h0 ed h2 fisse, al variare di g;

la Hash 4 al variare di g produce numeri sempre differenti e produce numeri poco differenti con h0 e h2 variabili e g fissata.

La Hash 3 è un compromesso tra le due ed è quella con cui condurrò gran parte dei miei test. In ogni caso ho effettuato test anche con la Hash 1 e la Hash 4 per controprova di queste considerazioni.

Ho eseguito vari test per verificare:

I tempi di costruzione della tabella al variare della funzione Hash, del numero delle chiavi e di r

Il numero dei backtracking ed il numero dei ricalcoli.

Sono stati fatti anche test utilizzando tecniche di backtracking "interno", ovvero nella funzione CreaHash stessa, ma non sono riportati in quanto non significanti: i tempi ottenuti non sono affatto accettabili, anche se è presumibile che quando il numero delle chiavi cresce di molto oltre il mio limite massimo (16000) potrebbe essere utile considerare un backtracking "interno" quando si arriva alle ultime K-Liste. Cominciamo con i test effettuati con la Hash 3.

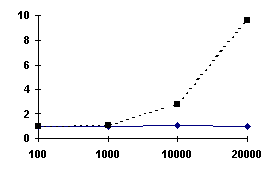
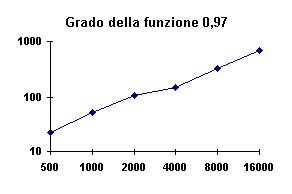
Figura -4 - Tempi (s) di creazione tabelle Hash con r minimo

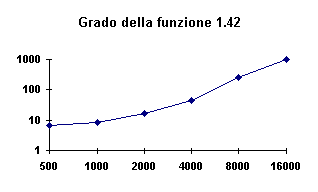
La funzione presenta un andamento non del tutto lineare: grado = 1.42, ma dal grafico sembra evidenziarsi un andamento quadratico che fuori dalla scala logaritmica indica un andamento esponenziale. Questo è dovuto in parte al numero delle prove, in parte alla variazione di r ed in ogni caso il tutto è attribuibile solo al numero di backtracking esterni effettuati, in quanto il tempo che ogni chiamata a CreaHash cresce linearmente come si vede nella figura successiva. D’altra parte con la variazione di r verso il valore minimo è ragionevole aspettarsi un aumento dei tempi.

Figura -5 - Tempi necessari per una chiamata a CreaHash (ms) con r minimo

 

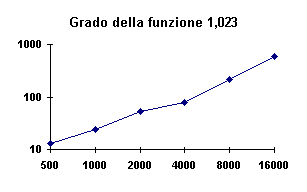
Oltre al tempo per creare la tabella ho contato anche il numero di chiamate a CreaHash ed il numero di ricalcoli (vedi Tabella 3*). I tempi rappresentati nella figura di sopra sono quelli necessari per effettuare una chiamata a CreaHash e quindi si vede che, in condizioni ideali o comunque con un numero di prove infinito, la crescita è nettamente lineare (grado = 1,023), anche se notiamo uno scostamento per valori elevati a causa della variazione di r che inizia farsi sentire. Le stesse prove sono state fatte utilizzando un valore di r costante ed elevato pari ad n/2.

Figura -6 - Tempi (ms) di creazione della tabella Hash con r costante

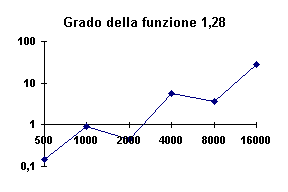
Il grado di questa funzione è circa 1,28 e quindi non molto lineare, ma questo è dovuto probabilmente a causa di due valori molto incerti, per 2000 e 8000 chiavi. In ogni caso la costanza di r ha portato il tutto verso una maggiore linearità rispetto alla Figura V-4 *

Figura -7 - Tempi (ms) di chiamata della funzione CreaHash con r costante

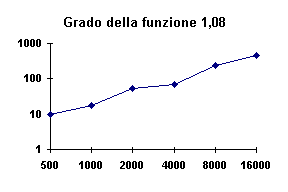
Si nota che sono gli stessi della Figura V-6 (grado di questo 1,08). Anche per questo caso è stato calcolato il numero di backtracking e il numero di ricalcoli: vedi Tabella 1 *. Di seguito vediamo come quando r tende al valore minimo i tempi salgono bruscamente.

Figura -8 - Tempi(s) searching al variare di r con n costante

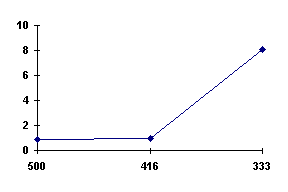
Questi dati fanno riferimento alla Tabella 5, *. Come si può notare avvicinandosi al valore minimo i tempi subiscono una forte impennata. Vediamo adesso i tempi globali attraverso alcuni grafici cumulativi in scala logaritmica.

Figura -9 - Tempi (ms) cumulativi nelle varie fasi

 

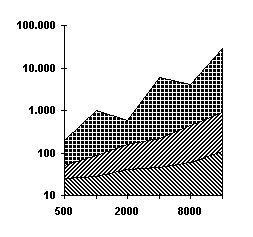
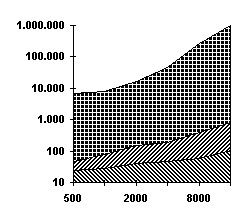
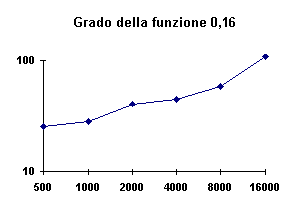
Qui possiamo notare in scala logaritmica i tempi delle tre fasi: dal basso verso l’alto troviamo Mapping, Ordering e Searching. Si può notare che c’è un ordine di grandezza di differenza tra i due grafici che hanno rispettivamente r costante pari ad n/2 e r minima. Notiamo altresì che la velocità con cui crescono i tempi è sempre maggiore: si va dalla quasi costanza del Mapping (grado = 0.18) fino alla scarsa linearità del Searching (grado = 1.3 circa). Questi grafici riassumo i dati della Tabella 6* e della Tabella 7*.

Detto ciò, considerando che i tempi per il Mapping e l’Ordering non dipendono dalla funzione Hash vediamo quali risultati otteniamo con le funzioni Hash 1 ed Hash 4 nel caso specifico in cui r è numkey/2 e confrontiamo con gli stessi dati ottenuti dalla Hash 3. Vedremo che i risultati di cui al paragrafo 7 * troveranno conferma.

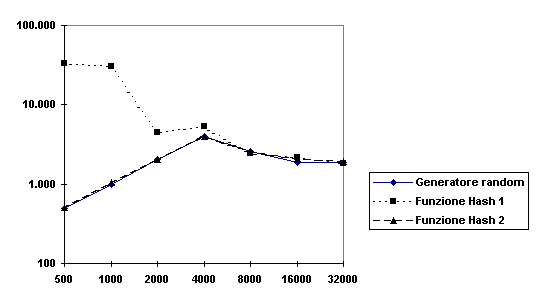
Figura -10 - Confronto tra funzioni Hash

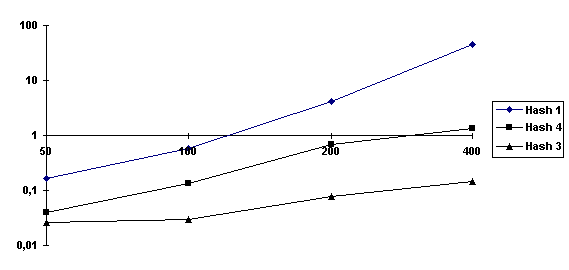
Ricordo che la Hash 3 è data dall’Espressione V-6*, la Hash 4 dall’Espressione V-5* e la Hash 1 dall’Espressione II-1*. Notiamo che la crescita della Hash 1 sembra essere quadratica nel grafico, cioè esponenziale nella realtà, in ogni caso il grado del polinomio che si ottiene è 3,27. Le altre due crescono abbastanza linearmente sul grafico. Tuttavia questo per la Hash 4 corrisponde ad un grado pari a 1,67 e quindi possiamo parlare di crescita quadratica. Per la Hash 3 otteniamo un grado 1,12 abbastanza lineare: anzi è il migliore ottenuto e questo conferma che se r è costante la crescita è poco più che lineare.

In conclusione posso dire che:

la migliore funzione hash è la Hash 3 data dall’Espressione V-6* in quanto non solo presenta i tempi più bassi rispetto alle altre, ma in ogni caso il grado che si ottiene è il più piccolo rispetto alle altre funzioni. Da escludere la Hash 1 che si è rivelata, come previsto dalla misure di VDC e VDU del tutto inutilizzabile anche per il comportamento quasi esponenziale dei tempi nella fase di Searching: ad esempio non sono mai riuscito a far calcolare una tabella di 1000 elementi.

Il comportamento trovato è poco più che lineare (NlogN?). Questo si trova considerando i due casi ad r costante in cui abbiamo trovato un grado minore di 1,3. Questo è in linea con quanto previsto teoricamente a parte la differente funzione Hash. Gli altri tempi, trascurabili in ogni caso, crescono comunque al massimo linearmente o sub-linearmente.

Non sembra rendersi utile un meccanismo di backtracking interno alla funzione CreaHash, se non per valori molto maggiori di quelli da me considerati. Questo comunque porta ad un minor numero di backtracking esterni, anche se cresce notevolmente il tempo per una chiamata a CreaHash. Tuttavia è semplice dimostrare che se si continua a prendere il valore più piccolo per r, la probabilità di allocare l’ultima K-Lista tende a 0 quando numkey tende ad infinito. Ovvero all’aumentare del numero delle chiavi potrebbe essere utile cercare di ricominciare dagli ultimi gruppi invece che dal primo per amplificare questa probabilità.

La dipendenza tra r e numkey è molto stretta: per quanto sembra è impossibile scendere sotto il valore indicato come minimo ed anzi avendo a disposizione molta memoria sarà opportuno tenere alto r anche e sopra numkey/2: i tempi decadono esponenzialmente.

VI. Allegati

Tabella 1- Risultati test casualità

Tabella 2 - Tempi nelle varie fasi iniziali (MAPPING e ORDERING)

Tabella 3 - Risultati del test di creazione tabella con r minimo

Tabella 4 - Risultati del test di creazione tabella con r costante pari a n/2.

Tabella 5 - Risultati al variare di r con n = 1000 costante

Tabella 6 - Tempi complessivi (ms) con r costante

Tabella 7 - Tempi complessivi (ms) con r minima

Tabella 8 - Confronto tra le funzioni Hash

Tabella 9 - Verifica della casualità delle funzioni Hash al crescere del numero delle chiavi

Tabella 10 - Valori di VDC e VDU per le varie funzione Hash con numkey = 50