Il Teorema di Fermat
Questa sezione si suddivide:
Cliccando qui invece tornate alla mia HomePage
Introduzione
Dunque come tutti sanno dati due numeri naturali, per semplicita' a e b si ha che esiste sempre unico c tale che
a + b = c
(dati 2 e 3 esiste unico 5 per cui 2+3 = 5. Partendo dagli assiomi fondamentali dei numeri naturali che garantiscono l'esistenza, si puo' dimostrare l'unicita'. Tanto per divertivi ecco la dimostrazione che quel numero z per cui a + z = a, chiamato in genere zero e' unico(esiste davvero, non e' uno scherzo!!). Per assurdo sia z' per cui a + z' = a con z' differente da z. Allora se scegliamo a = z si ha z + z' = z, ma anche z' + z = z' quindi z=z' assurdo peche' si erano supposti differenti, quindi lo zero e' unico)
Fino adesso e' un po' la scoperta dell'acqua calda. Pitagora dimostrò che la somma dei
quadrati costruiti sui cateti e' uguale al quadrato costruito sull'ipotenusa (se volete qui c'è una prova).
Questo teorema lo si puo' vedere da un punto di vista geometrico (costruendo fisicamente i
quadrati) ed allora si può dimostrare che vale per un qualunque poligono regolare di lato
n (ad esempio gli la somma dell'area degli eptagoni costruiti sui cateti e' uguale alla
somma dell'eptagono costruito sull'ipotenusa, dove l'eptagono e' il poligono regolare con
sette lati).
Se lo osserviamo da un punto di vista piu' algebrico si ha che detti a,b,c le misure dei
lati vale a^2 + b^2 = c^2. Interessante e' notare come questo teorema portò storicamente
alla scoperta dei numeri irrazionali, ovvero numeri non esprimibili come rapporto tra due
numeri interi, ovvero numeri che ammettono una rappresentazione infinita non periodica,
... Ad esempio se considerate il triangolo rettangolo isoscele (con due lati uguali che
non possono che esseri i cateti) di cateto 1 si ha che l'ipotenusa vale radice quadrata di
2. Questo numero e' irrazionale (pare che Pitagora fosse convinto della loro inesistenza e
la leggenda narra che il suo allievo che fece questa scoperta, una conseguenza immediata
del teorema, venne annegato). In genere il risultato di una radice quadrata e' un numero
irrazionale (a meno che non sia un quadrato, come il 4). Questi numeri si dicono
irrazionali algebrici, per distinguerli dagli irrazionali transcendenti, come il pi greco,
il numero di Nepero,...
Abbiamo gia' detto che esistono infinite terne di numeri naturali per cui a+b = c.
Pitagora ha dimostraro che esistono infinite terne di numeri naturali per cui a^2 + b^2 =
c^2. Ad esempio 3,4,5 (9 + 16 = 25).
Sono terne anche i loro multipli 6,8,10; 9,12, 15;... Se consideriamo fondamentali quelle
terne per cui il massimo comun divisore tra i tre numeri e' 1 (ad esempio 3,4,5) allora
vale:
Dato n pari si ha la terna 2n, n^2-1, n^2+1 comunque si scelga n. Inoltre MCD(2n,
n^2-1, n^2+1) = 1 in quanto 2n e' pari mentre n^2-1 e' dispari.
Dato n dispari si ha la terna n, (n^2-1)/2, (n^2+1)/2 comunque si scelga n. Inoltre MCD(n,
(n^2-1)/2, (n^2+1)/2) = 1 in quanto n e' dispari, mentre o (n^2-1)/2 o (n^2+1)/2 e' pari.
Infatti la loro differenza e' 1 (sono cioe' due numeri consecutivi).
Quindi le prime terne fondamentali sono:
| 3 | 4 | 5 |
| 8 | 15 | 17 |
| 5 | 12 | 13 |
| 12 | 35 | 37 |
| 7 | 24 | 25 |
| 16 | 63 | 65 |
Ben presto si penso' ad un'estensione.
Teorema di Fermat
Abbiamo visto che esistono infinite terne per cui a^2+b^2 = c^2; ed erano anche infinite quelle per cui a+b =c. Se uno cerca di estrapolare da questi due casi il caso generico con a^k + b^k = c^k dovrebbe concludere che le terne sono sempre infinite.
Non provate a cercarle o a farle cercare dal vostro computer perche' ecco cosa scrisse (piu' o meno) il grande matematico Fermat a margine del "Aritmetica" di Diofanto di Alessandria, dove parlava delle terne pitagoriche.
Non esiste nessuna terna a,b,c di numeri naturali per cui a^k+b^k= c^k se k e' numero naturale maggiore di due.
Chi l'avrebbe detto? Di seguito ci si aspettava di trovare la dimostrazione invece Fermat scrisse: "ho una dimostrazione veramente meravigliosa di questa proposizione, ma il margine e' troppo piccolo per contenerla". Lui non era nuovo a cose del genere e tutti gli altri teoremi proposti in modo simile furono in breve dimostrati. Ma non questo che quindi viene chiamato l'ultimo teorema di Fermat, nel senso di ultimo da provare. Vari matematici cercarono la soluzione: addirittura Eulero, grande matematico del '700 arrivò a far perquisire la casa che fu di Fermat in cerca di una traccia di quella dimostrazione!
Mancando una dimostrazione per circa trecento anni si brancolo' nel buio finche' un matematico a fine ottocento dimostro' che se queste terne esistono sono al piu' un numero finito. Sembrava proprio che il vecchio avesse avuto il giusto intuito, ma sono trascorsi altri cento anni prima che qualcuno dimostrasse il suo teorema. La dimostrazione e' del 1994 di J. Wiles attraverso strumenti matematici sconosciuti naturalmente a Fermat (ed anche a me :-( ). E' stata cosi' svelata una stranissima proprieta' dei numeri naturali che per comprendere dovremmo leggere e capire la dimostrazione (e forse non sara' sufficiente a farci capire quale sia il motivo che separa il 2 dal 3, cioe' a^2+b^2 = c^2, va bene; a^3+b^3 = c^3, non va bene...)
Se sapete nuove notizie a questo proposito fatemele
sapere![]() , altrimenti potete tornare alla HomePage
, altrimenti potete tornare alla HomePage
Teorema di Pitagora
Dimostrazione (una delle oltre 300, forse la stessa fatta dalla scuola di Pitagora). Volendo potete farla sulla sabbia come gli antichi greci, o comunque utilizzando solo riga e compasso. Dove la riga naturalmente non riporta alcuna misurazione (come un pezzo di legno)
Considerate due quadrati uguali qualsiasi e suddivideteli come indicato:
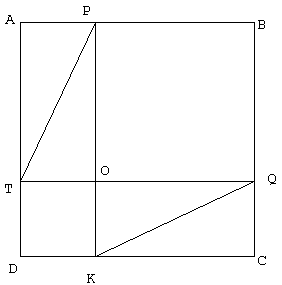
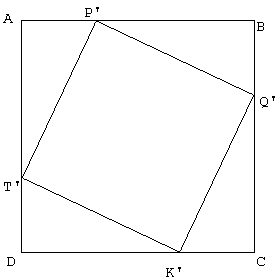
In modo che AP = QC = DK = TD = TO = OK = DT' = AP'= BQ'= K'C ed anche PB = BQ = KC = AT = PO = OQ = AT' = P'B = Q'C = DK'. Si puo' fare in quanto i due quadrati sono uguali.
Si nota subito che la somma delle aree di AP'T' + T'DK' + K'CQ' + Q'BP' = APOT + OQCK. Infatti per esempio il triangolo POT e' uguale al triangolo P'BQ' in quanto PO = P'B; BQ' = TO e l'angolo POT e' uguale all'angolo P'BQ'. Quest'ultimo e' ver: infatti TO = DT = DK = OK e l'angolo in D e' retto per costruzione, allora DTOK e' un quadrato, ma anche POBQ e' un quadrato e poiche' l'angolo POT e' opposto, quindi uguale all'angolo KOQ, POT e' retto quindi uguale a P'BQ'.
Per cui se togliamo ad entrambi i quadrati queste aree cio' che rimane sara' uguale: cio' che rimane nel primo quadrato e' la somma dei quadrati costruiti sui cateti, cio' che rimane nel secondo e' il quadrato costruito sull'ipotenusa. Questo e' un quadrato in quanto i triangoli T'AP' = P'BQ' = Q'CK' = K'DT', quindi le ipotenuse sono tutte uguali; inoltre l'angolo T'K'Q' = 180° - T'K'D - Q'K'C, ma Q'K'C = K'T'D, poiche' i triangoli sono uguali. Allora T'K'Q' = 180° - T'K'D - K'T'D, ma la somma degli angoli interni di un triangolo e' 180°, ovvero 180° = T'DK' + DT'K' + T'K'D, con T'DK' = 90° per costruzione. Allora T'K'D + K'TD = 90°, allora T'K'Q' = 180° - 90° = 90°. Se nel rombo T'K'Q'P' un angolo e' retto, anche tutti gli altri lo sono, quindi e' un quadrato. Come volevasi dimostrare.