[Home] [Research] [NOMaD] [ETBib] [Publications] [Students] [Links] [CV]

Minimum cost routing and wavelength allocation using a genetic-algorithm/heuristic hybrid approach

M. C. Sinclair

Proc. Sixth IEE Conf. on Telecommunications, Edinburgh, UK, March/April 1998

Introduction

This paper describes early results in minimum cost routing and wavelength allocation of multi-wavelength all-optical transport networks using a genetic-algorithm (GA)/heuristic hybrid approach. The results were obtained using a tool for optical network optimisation, modelling and design (NOMaD) developed by the author, see Sinclair (1, 2).

NOMaD is used as part of the author's research into the application of GA/heuristic hybrid optimisation techniques to network design, as well as in several research projects at Essex, including two under the European Commission funded research programme in Advanced Communications Technologies and Services (ACTS): WOTAN (Wavelength-agile Optical Transport and Access Network) and OPEN (Optical Pan-European Network); and the Fujitsu Telecommunications Europe Ltd. ``Future Broadband Networks'' project.

Wavelength Allocation

Although NOMaD has previously been used on multi-wavelength all-optical networks by Sinclair for virtual topology design (2), the focus here is on minimum cost routing and wavelength allocation. It is assumed that node (optical cross connect) locations have been selected, and a suitable topology determined, including the number of fibres available in the links (cables) between node pairs. Further, that the static traffic requirements need to be allocated to as many 10 Gbit/s (duplex) wavelength channels as required, each of which will be routed independently on a single wavelength, end-to-end (i.e. wavelength-path routing). In addition, although some authors have included failure restoration and restrictions on the number of wavelengths per fibre, see Nagatsu et al. (3), for simplicity, these will not be considered here.

Many authors have considered a low network wavelength requirement (i.e. the number of distinct wavelengths in the network) to be desirable as a design objective due to the technological limitations, and resulting cost implications, of carrying more than a small number of wavelengths over national or even international distances. However, an objective that consists of a simplified assessment of the cost of the whole network including, at an appropriate level, the cost of exceeding the minimum network wavelength requirement, is arguably superior, and is the approach used here.

This problem and its variants have attracted considerable interest recently, with a variety of solution approaches including heuristics, genetic algorithms and mathematical programming. To provide benchmarks against which to compare the GA/heuristic hybrid approach adopted here, three recent wavelength allocation algorithms have been selected.

Wuttisittikulkij and O'Mahony (4) developed a simple, fast and non-iterative algorithm, which works with k-lowest hop count paths to obtain a low network wavelength requirement. Wauters and Demeester (5) describe two algorithms, one based on a version of Dijkstra's algorithm modified such that in `extend[ing] an already found part of a route, only those arcs are considered which have a wavelength channel free which is available on all [links] of the already found part of the route'; this algorithm produces a low-cost allocation, whilst also keeping network wavelength requirement low. Their second algorithm (HRWA), is based on iterative application of a modified version of Yen's k-shortest path algorithm, and aims to produce the lowest cost allocation that still achieves minimum network wavelength requirement.

Cost Model

The cost model used is a development of one suggested by Sinclair (6). To determine the cost of a given network, separate models for both links and nodes are required.

Given the network paths, the capacity of link $(i,j)$ is taken to be:

V_{ij} = \lambda_{ij}V_{\lambda}

where $\lambda_{ij}$ is the total number of wavelengths in use on the link (i.e. across all its fibres) and $V_{\lambda}$ is the granularity of the wavelength channels (i.e. 10Gbit/s). The wavelength-requirement capacity of link $(i,j)$ is taken to be:

V_{\lambda,ij} = \lambda_{\mathrm{req},ij}F_{ij}V_{\lambda}

where $\lambda_{\mathrm{req},ij}$ is the wavelength requirement of link $(i,j)$ (i.e. the highest wavelength number of any fibre on the link) and $F_{ij}$ is the number of fibres in use on link $(i,j)$. The wavelength-requirement capacity is thus the capacity that would result if all the dark wavelengths on all the (partially-used) fibres of the link were filled, up to the current link wavelength requirement. The capacity cost of link $(i,j)$ is:

C_{V,ij} = V_{ij}^{\alpha}L_{ij}

where $\alpha$ is a constant and $L_{ij}$ is the length of link $(i,j)$ in km. The wavelength-requirement cost of link $(i,j)$ is:

C_{\lambda,ij} = V_{\lambda,ij}^{\beta}L_{ij}

where $\beta$ is a constant. The overall cost of link $(i,j)$ is then taken to be:

C_{ij} = \gamma C_{V,ij} + (1-\gamma) C_{\lambda,ij}

where $\gamma$ is a constant ($0 \leq \gamma \leq 1$). With $\gamma = 0$, the link model only takes account of the capacity used, and ignores the link wavelength requirement; whereas, with $\gamma = 1$, the actual capacity used is ignored, and the focus is entirely on the wavelength requirement. An intermediate value of $\gamma$, such as 0.5, is regarded as being more representative of the actual costs involved.

For the nodes, a node effective distance was used as a way of representing the cost of nodes in an optical network in equivalent distance terms. It can be regarded as the effective distance added to a path as a result of traversing a node. Although Sinclair (6) used it to influence the selection of paths in minimum cost virtual topology design, thereby reflecting the relatively high costs of optical switching, here it is only used as part of the node cost model. The node effective distance of node $i$ was taken to be:

N_i = K_{0} + n_{i}K_{n}

where $n_{i}$ is the degree of node $i$, i.e. the number of links attached to it. The constants $K_{0}$ and $K_{n}$ were taken to be 200km and 100km respectively. Node effective distance thus increases as the switch grows more complex. Node capacity is the sum of the effective capacities of all the attached links, where the effective capacity of link $(i,j)$ is given by:

V_{e,ij} = \gamma V_{ij} + (1-\gamma)V_{\lambda,ij}

The node capacity is therefore dependent to some extent on the wavelength requirements of its attached links. The node cost was then taken to be:

C_{i} = 0.5N_{i}V_{i}

where $V_{i}$ is the capacity of node $i$ in Gbit/s. The cost is thus derived as if the node was a star of links, each of half the node effective length, and each having the same capacity as the node itself.

The network cost is then taken to be the sum of the costs of all the individual links and nodes comprising the network. However, the actual metric used also includes a penalty (say 250,000) added for each individual traffic requirement unsatisfied, to avoid the false minimum of carrying no traffic at all, which would otherwise have a network cost of zero.

GA/Heuristic Hybrids

The simple or `traditional' GA is based on a simplification of the mechanisms of natural selection and genetics. It uses a population of binary strings, each one of which encodes a potential solution in the problem space. Every generation, the fitness of the strings is determined by decoding them and assessing their worth as solutions; the strings then reproduce in accordance with their fitness, with some strings exchanging part of their genetic material (crossover), and all strings subject to small perturbations at low probability (mutation); the new population of child strings then replaces the old. This process continues until a stopping condition, such as a maximum number of generations, is reached; the solution corresponding to the best string found in the course of a run is taken as the result. For more details, see Goldberg (7).

However, within the field of GA research, there are two `schools of thought' with respect to GAs. One approach is to try and develop an algorithm that is robust and general in its application i.e. it makes use of no problem-specific information---the focus of the research is on the development of a better GA for all problems, see Goldberg (7). The other is to blend the traditional GA with problem-specific operators (complementing or replacing crossover and mutation), often based on existing heuristic algorithms for a particular problem (or problem domain), such that the combined algorithm performs better than either a `pure' GA or the heuristic alone, see Davis (8). This latter approach is more pragmatic in nature, with the better solution of particular engineering problems being the primary focus of research.

The GA/heuristic hybrid approach thus adopts a problem-specific encoding, and then develops and employs problem-specific operators that together combine the best existing heuristics for the problem with an overall GA framework. The motivation for this approach is simple, according to Davis (8): ``Although genetic algorithms using binary representation and single-point crossover and binary mutation are robust algorithms, they are almost never the \textbf{best} algorithms to use for any [specific] problem''. It is almost always possible to develop a problem-specific heuristic/GA hybrid that will outperform either the heuristic or a traditional GA alone, and this is one of the approaches that is used in NOMaD.

For a brief survey of work on the application of GAs to network design, see Proestaki and Sinclair (9), which indicates that even without the incorporation of heuristic-based operators, GAs are often able to match heuristics alone in terms of results, if not in speed. Building on this promise, GA/heuristic hybrids should prove even better for network design.

The Algorithm

NOMaD's toolset represents networks as objects, coded in C++, composed not only of nodes, links and ordered sequences of paths, but also objects representing the network's adjacency matrix, connection matrix (which records link levels in hierarchical networks) and the traffic requirements. In addition, networks include additional objects to represent the cable, fibre and wavelength-routed structure of a multi-wavelength optical network. Consequently, within NOMaD, rather than using a binary representation, network objects are themselves the structures undergoing adaptation---a highly-structured and very problem-specific representation that requires no decoding or interpretation.

Similarly, the GA is also implemented using object technology, with a population of individuals (simply consisting of a single network object and some additional accounting information) and an operator pool of operators. As in Davis (8), the probabilities of individual operators being applied to an individual adapt through the course of a run using a credit-assignment algorithm, rather than being chosen with a fixed probability throughout. Whenever an individual is created whose fitness exceeds that of the best individual up to the end of the previous generation, the improvement in fitness is credited to the operator responsible. In addition, a decreasing fraction of the credit (say, 0.5 and 0.25) is awarded to the parent operator (i.e. the operator that created this individual's parent) and grandparent operator, to ensure that two- and three-operator sequences are rewarded appropriately. After a few generations (say, 4), a small proportion (say, 0.15) of the operator probabilities is reassigned according to the average credit earned per child each operator has generated. In addition, operators are given a minimum probability (say, 0.05) to ensure they do not lose the opportunity to gain some credit if they, having decayed to the minimum level, are later found to be useful to further evolve the population.

A variety of operators have been incorporated within NOMaD including those used in this paper: wavelength-allocation path mutation (WKM), wavelength-allocation path single-point crossover (WKCO), wavelength-allocation path reroute operator (WWRR) and wavelength-allocation path shift-out operator (WWSO).

Path mutation simply selects a path at random from the k-shortest paths (where k is an operator parameter), and routes the requirement on the lowest available wavelength on that path (irrespective of fibres used).

Path single-point crossover operates on two networks. The first is modified such that up to a randomly selected individual requirement (considered in order of their end node ids), all the paths remain unchanged, but from then on the paths used are those in the second network, except that the lowest wavelength actually available is used in each case. (However, if any requirement was unsatisfied in the second network, then a random k-shortest path is used instead.) The second network undergoes the complementary recombination.

The path reroute operator locates the first path in the network which has the highest wavelength number (found by searching the cables in order of their end node ids), and attempts to reroute it on a lower (and the lowest available) wavelength number using one of the k-shortest paths (where k is an operator parameter, and the shortest path is selected if there is more than one at the lowest available wavelength number). It is based on Step 2a in Wauters and Demeester's HRWA algorithm (5).

The path shift-out operator locates the first path in the network which has the highest wavelength number, and attempts to shift it to a lower wavelength number by shifting out (rerouting) all the paths blocking that particular wavelength number. The wavelength chosen is the one that results in the smallest increase in overall path length, given the constraint that all rerouting must be to lower wavelength numbers than the original wavelength of the path being shifted down. It is based on Step 2b in Wauters and Demeester's HRWA algorithm (5).

Experimental Results

For the relative assessment of heuristic and GA/heuristic hybrid approaches to minimum cost routing and wavelength allocation, it was decided to use five test networks (see Fig. 1). The initial node locations and traffic requirements were generated using the approach described by Griffith et al. (10), although further modified to ensure reasonable node separations. Each network has fifteen nodes, covers a 1,000 km x 1,000 km area and carries an overall traffic of 1,500 Gbit/s. The network topologies used are the best obtained using the GA/heuristic hybrid algorithm described by Sinclair (2), or better results obtained since, with each link consisting of two fibres.

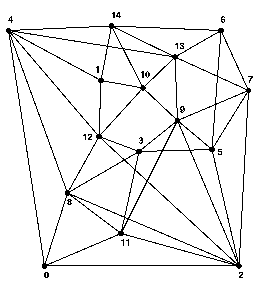Network 1 Network 2
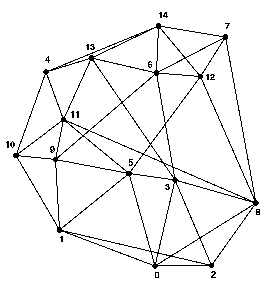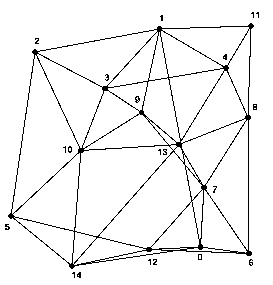Network 3 Network 4
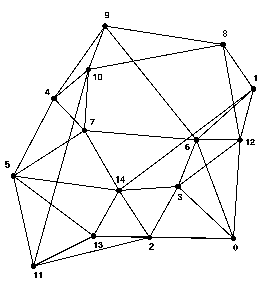Network 5

Figure 1: Test Networks

The GA/heuristic hybrids applied had a population size of 500, a maximum of 100,000 trials, and used tournament selection (of size 4). The operators, and their initial probabilities, are given in Table 1. The latter were selected by a few trial runs, aiming for settings that would remain approximately constant for 50 or so generations. It could be argued that such starting values best promote high quality solutions, by approximately matching operator probabilities to their initial productivities. Throughout, the operator-probability adaptation algorithm parameters were set to the values suggested above.

Table 1 - Initial operator probabilities
GA WKM WKCO WWRR WWSO
1 0.05 0.25 0.15 0.45
2 0.05 0.30 0.10 0.40
3 0.05 0.20 0.25 0.40

The hybrids were each applied five times with different random seeds (i.e. best of five runs) to the five test networks, with $\gamma$ set to 0.5, 1 and 0 for GA1, GA2 and GA3, respectively; in all cases both $\alpha$ and $\beta$ were set to 1.0. In addition Wuttisittikulkij and O'Mahony's heuristic (sorted order; best of five runs) (4) (W&O), Wauters and Demeester's (5) modified Dijkstra based heuristic (W&D1) and their HRWA heuristic (W&D2) were applied to each network for each value of $\gamma$. For both the hybrids and heuristics, k was set to 8 throughout. The results are given in Tables 2, 3 and 4, with the lowest cost in each table for a given network shown in bold.

Table 2 - Network cost for $\gamma = 0.5$
Network W&O W&D1 W&D2 GA1
x 10^6 x 10^6 x 10^6 x 10^6
1 5.909 6.007 6.358 5.579
2 5.151 5.241 5.278 4.886
3 5.153 5.707 5.637 4.976
4 5.413 5.528 5.765 5.117
5 5.424 5.773 5.658 5.108
Table 3 - Network cost for $\gamma = 1$
Network W&O W&D1 W&D2 GA2
x 10^6 x 10^6 x 10^6 x 10^6
1 5.704 5.172 5.896 4.994
2 5.081 4.589 5.046 4.436
3 5.051 4.625 5.446 4.394
4 5.313 4.808 5.388 4.645
5 5.302 4.806 5.326 4.640
Table 4 - Network cost for $\gamma = 0$
Network W&O W&D1 W&D2 GA3
x 10^6 x 10^6 x 10^6 x 10^6
1 6.036 6.843 6.820 6.116
2 5.213 5.893 5.510 5.228
3 5.229 6.789 5.828 5.362
4 5.503 6.247 6.142 5.499
5 5.544 6.740 5.991 5.523

For $\gamma = 0.5$, a value regarded as being reasonably representative of actual costs, the best heuristic was found to be W&O, which is thus providing a good trade-off between capacity cost and link wavelength requirements. Nevertheless, for all five networks the lowest network costs were actually obtained by the hybrid algorithm, GA1 (Table 2).

With $\gamma = 1$, focusing the network cost on capacity rather than wavelength requirement, the best heuristic was W&D1, and by a wide margin; this is perhaps to be expected, as W&D1 uses shortest paths, thereby placing the emphasis on cost over wavelength requirement, rather than k-lowest hop count or k-shortest paths, as do W&O and W&D2. However, once again, the hybrid algorithm, GA2, provided the best results for all five networks (Table 3).

Finally, setting $\gamma = 0$, so that the network cost depends entirely on the link wavelength requirements, the best heuristic was W&O; this is no doubt due to the superiority of W&O, with respect to network wavelength requirement, compared to the other two heuristics. (Unpublished comparison on the basis of network wavelength requirement.) Disappointingly, however, the hybrid algorithm, GA3, was only able to obtain the best overall cost for two networks, although its results were close to those of W&O on the other three (Table 4).

Conclusions & Further Work

The use of a genetic-algorithm (GA)/heuristic hybrid approach for minimum cost routing and wavelength allocation in multi-wavelength all-optical transport networks has been described. The experimental results show that the GA/heuristic hybrid approach is as promising as has been hoped, as in competition with three recent heuristics, it was able to obtain the lowest network costs for $\gamma$ set to both 0.5 and 1; and in the case of $\gamma = 0$, was able to match the results of the best heuristic yet implemented by the author. It is anticipated that, as well as further exploring both those operators already developed and the operator-probability adaptation algorithm, future work will investigate additional heuristic operators, the impact of non-linear link-cost models (i.e. $\alpha \neq 1, \beta \neq 1$) and combining both topology and wavelength allocation into a single design process.

Acknowledgements

The author is grateful to Prof. Rob Massara for his guidance of my Ph.D. project, and to Katerina Proestaki and Noel Parnis (all three from E.S.E., University of Essex) for the many interesting and stimulating discussions during the continuing development of NOMaD. Ms. Proestaki was until recently supported by the European Commission on ACTS project AC029 (WOTAN), but is now the Fujitsu Research Fellow. Mr. Parnis is supported by ACTS project AC066 (OPEN).

References

  1. Sinclair, M.C., 1996, ``NOMaD: Initial architecture of an optical network optimisation, modelling and design tool'', Proc. 12th UK Performance Engineering Workshop University of Edinburgh, 157-167

  2. Sinclair, M.C., 1997, ``NOMaD: Applying a genetic-algorithm/heuristic hybrid approach to optical network topology design'', Proc. Intl. Conf. on Artificial Neural Networks and Genetic Algorithms (ICANNGA'97), Norwich, UK, 301-305

  3. Nagatsu, N., Okamoto, S. & Sato, K.I., 1996, ``Optical path cross-connect system scale evaluation using path accommodation design for restricted wavelength multiplexing'', IEEE J. Select. Areas Commun., 14, 893-902

  4. Wuttisittikulkij, L. & O'Mahony, M.J., 1995, ``A simple algorithm for wavelength assignment in optical networks'', Proc. 21st Eur. Conf. on Opt. Comm. (ECOC'95), Brussels, 859-862

  5. Wauters, N. & Demeester, P., 1996, ``Design of the optical-path layer in multiwavelength cross-connected networks'', IEEE J. Select. Areas Commun., 14, 881-892

  6. Sinclair, M.C., 1995, ``Minimum cost topology optimisation of the COST 239 European optical network'', Proc. Intl. Conf. on Artificial Neural Networks and Genetic Algorithms (ICANNGA'95), Ales, France, 26-29

  7. Goldberg, D.E., 1989, ``Genetic Algorithms in Search, Optimization and Machine Learning'', Addison-Wesley

  8. Davis, L., 1991, ``Handbook of Genetic Algorithms'', Van Nostrand Reinhold

  9. Proestaki, A. & Sinclair, M.C., 1996, ``Initial survey of heuristics for optical core network design in ACTS WOTAN'', Proc. 13th UK Teletraffic Symposium, University of Strathclyde, Glasgow, 20/1-20/8

  10. Griffith, P.S., Proestaki, A. & Sinclair, M.C., 1996, ``Heuristic topological design of low-cost optical telecommunication networks'', Proc. 12th UK Performance Engineering Workshop, University of Edinburgh, 129-140

Please feel free to comment on this page.
Creator: Mark C Sinclair <mcs@ieee.org>
Date: 14 vi 1999
[Home] [Research] [NOMaD] [ETBib] [Publications] [Students] [Links] [CV]
1