[Home] [Research] [NOMaD] [ETBib] [Publications] [Students] [Links] [CV]

Operator-probability adaptation in a genetic-algorithm/heuristic hybrid for optical network wavelength allocation

M. C. Sinclair

Proc. IEEE Intl. Conf. on Evolutionary Computation (ICEC'98), Anchorage, Alaska, USA, May 1998

Abstract

Operator-probability adaptation in a genetic-algorithm/heuristic hybrid for minimum cost routing and wavelength allocation of multi-wavelength all-optical transport networks is described. The hybrid algorithm uses an object-oriented representation of networks, and incorporates four operators: path mutation, single-point crossover, reroute and shift-out. The adaptation algorithm is based on that by Davis, but uses simplified operator accounting. Experimental results from three fifteen-node test networks, obtained using a tool for optical network optimisation, modelling and design (NOMaD), illustrate the interesting dynamic behaviour of the adaptation algorithm. They suggest that, in this application, with powerful problem-specific operators, the main benefits of operator-probability adaptation are in relieving the experimenter of the burden of setting initial probabilities and in the early performance of the hybrid, rather than in improvements of the final solution quality obtained.

Introduction

This paper describes an investigation into the use of operator-probability adaptation in a genetic-algorithm (GA)/heuristic hybrid for minimum cost routing and wavelength allocation of multi-wavelength all-optical transport networks. The results were obtained with a tool for optical network optimisation, modelling and design (NOMaD) developed by the author [1]. Although it has previously been used on multi-wavelength all-optical networks for virtual topology design [2] and wavelength allocation [3], the focus here is on NOMaD's operator-probability adaptation mechanism.

Operator-probability adaptation

Although most GAs use fixed operator probabilities, several researchers have described operator-probability adaptation algorithms. Tuson, in his extensive study [4], classifies these into two groups: co-evolutionary methods, that encode operator probabilities into each member of the population [5]; and learning-rule methods, that adapt the probabilities based on measurement of the operator productivities [6, 7, 8] (although another, more detailed, classification was recently proposed by Hinterding et al. [9]).

In the latter group, Davis' well-known mechanism [6] computes operator productivity by crediting operators with any improvement over the best member of the population; a decreasing fraction of this credit is also passed back to the operators responsible for creating the individual's parents, and so on, to a given depth. After a defined interval, the productivity of an operator is taken to be its total credit over the interval divided by the number of individuals it has created. Operator probabilities are then adjusted by reassigning a fraction of their probabilities in proportion to their productivity. Davis also mentions the possibility of preventing an operator's probability falling below an assigned minimum value, as well as the potential of his approach to measure the productivity of individual problem-specific heuristic operators.

More recently, Julstrom [7] presented ADOPP, an approach for steady-state GAs, in which all operators back to a given depth in an operator tree are credited with a decreasing fraction of any improvement over population median fitness. At all times, actual operator probabilities (and not just a fractional part) are determined by their recently earned credit. However, his study was limited to two-operator GAs, and provided no comparison with fixed operator probabilities.

Finally, Tuson & Ross [8] describe an investigation of Corne's COBRA (COst Based operator Rate Adaptation) algorithm, which instead of adjusting individual operator probabilities, assigns operators to a fixed set of probabilities according to their operator-productivity rank over a given interval. The operator productivity is determined by the average improvement of a child individual over its parent(s). Although COBRA has shown itself to be beneficial for timetabling problems, Tuson & Ross found it provided only equal or worse solution quality over a wide range of other test problems, compared with carefully chosen fixed operator probabilities (for both steady-state and generational GAs). They concluded that operator productivity (at least as Corne defines it) may misguide COBRA as, in some cases, although an operator's productivity is high, its preferred probability is low.

Wavelength allocation

In recent years there has been a growing interest in the potential of multi-wavelength all-optical transport networks to provide the huge bandwidths necessary if broadband services are widely adopted. One aspect of the design of such networks is determining the route and wavelength to be used by each of the individual traffic requirements. This problem and its variants have attracted considerable interest, with a variety of solution approaches including heuristics, GAs and mathematical programming.

Many authors have considered a low network wavelength requirement (i.e. the number of distinct wavelengths in the network) to be desirable as a design objective due to the technological limitations, and resulting cost implications, of carrying more than a small number of wavelengths over national or even international distances. However, an objective that consists of a simplified assessment of the cost of the whole network including, at an appropriate level, the cost of exceeding the minimum network wavelength requirement, is arguably superior, and is the approach used here (after [3], with $\alpha = 1.0$, $\beta = 1.0$ and $\gamma = 0.5$).

It is assumed that node (optical cross connect) locations have been selected, and a suitable topology determined, including the number of fibres available in the links (cables) between node pairs. Further, that the static traffic requirements need to be allocated to as many 10 Gbit/s (duplex) wavelength channels as required, each of which will be routed independently on a single wavelength, end-to-end (i.e. wavelength-path routing). In addition, although some authors have included failure restoration and restrictions on the number of wavelengths per fibre, for simplicity, these will not be considered here.

GA/heuristic hybrids

According to Davis: "Although genetic algorithms using binary representation and single-point crossover and binary mutation are robust algorithms, they are almost never the best algorithms to use for any [specific] problem" [6]. However, another possibility is to adopt a problem-specific encoding, and then develop and employ problem-specific operators that together combine the best existing heuristics for the problem with an overall GA framework. Using this approach, it is almost always possible to develop a problem-specific GA/heuristic hybrid that will outperform either the heuristic or a traditional GA alone.

Indeed, the recent work of the author has shown this to be the case for two aspects of optical network design: virtual topology design [2] and minimum cost routing and wavelength allocation [3]. For example, in the latter case, experimental results on five fifteen-node test networks suggest that a GA/heuristic hybrid algorithm provides superior results compared to three recent wavelength allocation heuristics, except when the network cost depends most heavily on wavelength requirement [3]. It is that same hybrid which is further investigated here.

The GA/heuristic hybrid algorithm

NOMaD represents networks as objects, coded in C++, composed not only of nodes, links and ordered sequences of paths, but also objects representing the network's adjacency matrix, connection matrix (which records link levels in hierarchical networks) and the traffic requirements. Further, networks include additional objects to represent the cable, fibre and wavelength-routed structure of a multi-wavelength optical network. Consequently, within NOMaD, rather than using a binary representation, network objects are themselves the structures undergoing adaptation---a highly-structured and very problem-specific representation that requires no decoding or interpretation.

Similarly, the GA is also implemented using object technology, with a population of individuals (each simply consisting of a single network object and some additional accounting information) and an operator pool of operators. A number of these operators have been incorporated within NOMaD including the four used in this paper [3]: wavelength-allocation path mutation (WKM), wavelength-allocation path single-point crossover (WKCO), wavelength-allocation path reroute operator (WWRR) and wavelength-allocation path shift-out operator (WWSO).

For a random requirement, path mutation simply reroutes on a randomly chosen $k$-shortest path (where $k$ is an operator parameter), using the lowest available wavelength on that path (irrespective of fibre choice).

Path single-point crossover operates on two networks. The first is modified such that up to a randomly selected individual requirement (considered in order of their end node ids), all the paths remain unchanged, but from then on the paths used are those in the second network, except that the lowest wavelength actually available is used in each case. (However, if any requirement was unsatisfied in the second network, then a random $k$-shortest path is used instead.) The second network undergoes the complementary recombination.

The path reroute operator locates the first path in the network which has the highest wavelength number (found by searching the cables in order of their end node ids), and attempts to reroute it on a lower (and the lowest available) wavelength number using one of the $k$-shortest paths (where $k$ is an operator parameter, and the shortest path is selected if there is more than one at the lowest available wavelength number). It is based on Step 2a in Wauters and Demeester's HRWA algorithm [10].

The path shift-out operator locates the first path in the network which has the highest wavelength number, and attempts to shift it to a lower wavelength number by shifting out (rerouting) all the paths blocking that particular wavelength number. The wavelength chosen is the one that results in the smallest increase in overall path length, given the constraint that all rerouting must be to lower wavelength numbers than the original wavelength of the path being shifted down. It is based on Step 2b in Wauters and Demeester's HRWA algorithm [10].

The adaptation algorithm

As a variety of operators are incorporated in NOMaD's different GA/heuristic hybrid algorithms, it might be thought necessary to determine appropriate operator probabilities for each of the distinct combinations of operators used. However, given the large computational effort that this would imply, instead the probabilities of individual operators being applied to an individual adapt through the course of a run using a credit-assignment algorithm, rather than being chosen with a fixed probability throughout.

As well as avoiding the need to determine appropriate fixed operator probabilities (except for the initial probabilities, which could be determined from a few trial runs), it was also hoped that there might be performance gains in allowing the probabilities to vary during the course of a run, such that the most appropriate blend of operators was used at each stage, as determined by the observed operator productivity.

The operator-probability adaptation algorithm adopted [2] is based on that of Davis [6]. Whenever an individual is created whose fitness exceeds that of the best individual found up to the end of the previous generation, the improvement in fitness is credited to the operator responsible. In addition, a decreasing fraction of the credit (say, $\kappa = 0.5$ and $\kappa^{2} = 0.25$) is awarded to the parent operator (i.e. the operator that created this individual's parent) and grandparent operator, to ensure that two- and three-operator sequences are rewarded appropriately. However, while Davis [6] maintained a complete tree (although of finite depth) of the operators responsible for the creation of an individual, here only a single (arbitrary) parent is recorded for binary operators. This greatly simplifies accounting, as instead of up to two parents, four grandparents, eight great-grandparents, etc., only a single parent and grandparent operator have to be recorded. Indeed, the overhead of maintaining and crediting a complete operator tree has already been noted elsewhere [4]. Further, although the selection of a single arbitrary parent operator means that all the operators responsible for a superior individual are not rewarded, nevertheless it would be expected that such operators would have subsequent opportunities to acquire credit, and it is their relative accumulation of credit, rather than the absolute value, that is important.

After a few generations (say, 4), a small proportion (say, $\psi = 0.15$) of the operator probabilities is reassigned according to the average credit earned per child each operator has generated. In addition, operators are given a minimum probability (say, 0.05) to ensure they do not lose the opportunity to gain some credit if they, having decayed to the minimum level, are later found to be useful to further evolve the population.

Experimental results

To investigate the use of operator-probability adaptation in a GA/heuristic hybrid for minimum cost routing and wavelength allocation, it was decided to use three test networks (Networks 1, 3 & 5 in [3]). The initial node locations and traffic requirements were generated using the approach described by Griffith et al. [11], although further modified to ensure reasonable node separations. Each network has fifteen nodes, covers a 1,000 km $\times$ 1,000 km area and carries an overall traffic of 1,500 Gbit/s. The network topologies used are the best obtained using the GA/heuristic hybrid algorithm described by Sinclair [2], or better results obtained since, with each link consisting of two fibres.

The GA/heuristic hybrids had a population size of 500, a maximum of 100,000 trials, used tournament selection (of size 4), and had $k$ set to 8 throughout.

In applying NOMaD to specific problems [2, 3], initial operator probabilities have so far been selected by a few trial runs, aiming for settings that would remain approximately constant for 50 or so generations. It was believed that such starting values would best promote high quality solutions, by approximately matching operator probabilities to their initial productivities. However, here, to avoid the potential bias of pre-tuned values, the initial probabilities of all four operators, and the reproduction (i.e. null) operator, REPR, have been set to 0.2.

To explore the influence of the adaptation proportion, $\psi$, three values were selected, 0.15, 0.00 and 0.30, and combined with a credit constant, $\kappa = 0.5$, these are denoted GA1, GA2 and GA3 in Table 1. The levels in GA1 are those that have been used by the author on specific applications [2, 3]; in GA2, the adaptation algorithm is completely deactivated, as with $\psi = 0.00$, the initial operator probabilities will remain unchanged for the entire run; GA3 represents a higher than usual rate of adaptation.

In examining the influence of the credit constant, the adaptation proportion was fixed to its usual value ($\psi = 0.15$), and $\kappa$ set to 0.5, 0.0 and 1.0 in GA1, GA4 and GA5 respectively (Table 1). While the usual value of $\kappa = 0.5$ allows reasonable credit to parent and grandparent operators, in GA4, credit is only awarded to the actual operator responsible for an improvement, whereas in GA5, the operator, parent and grandparent operators are all rewarded equally.

Table 1. Adaptation algorithm parameters
GA $\psi$ $\kappa$
1 0.15 0.5
2 0.00 0.5
3 0.30 0.5
4 0.15 0.0
5 0.15 1.0

Typical graphs of the changing operator probabilities during the course of a run for GA1, GA3, GA4 and GA5 are given in Fig. 1, 2, 3 and 4 respectively. All four graphs are for Network 1 with the same random seed, and hence have identical initial populations. A graph is not given for GA2, as the operator probabilities remain fixed at 0.2 throughout the run.

Figure 1

Figure 1. Operator probabilities for GA1

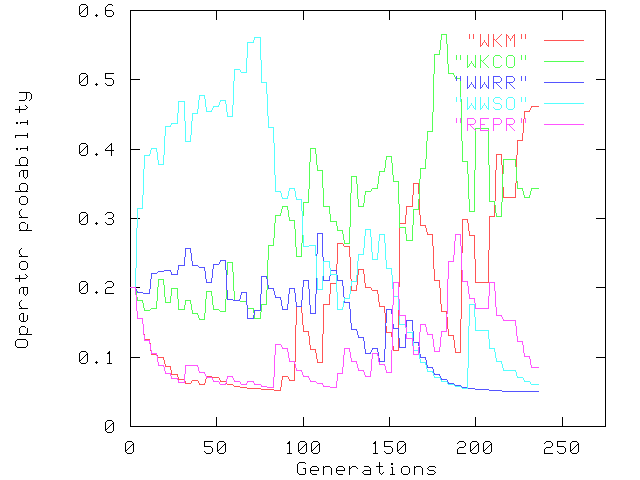Figure 2

Figure 2. Operator probabilities for GA3

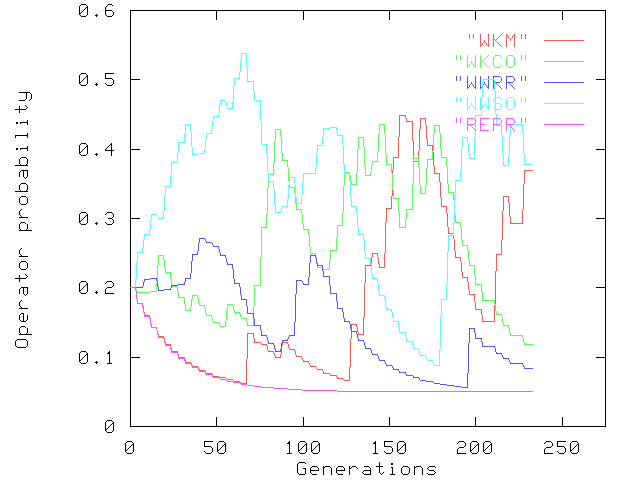Figure 3

Figure 3. Operator probabilities for GA4

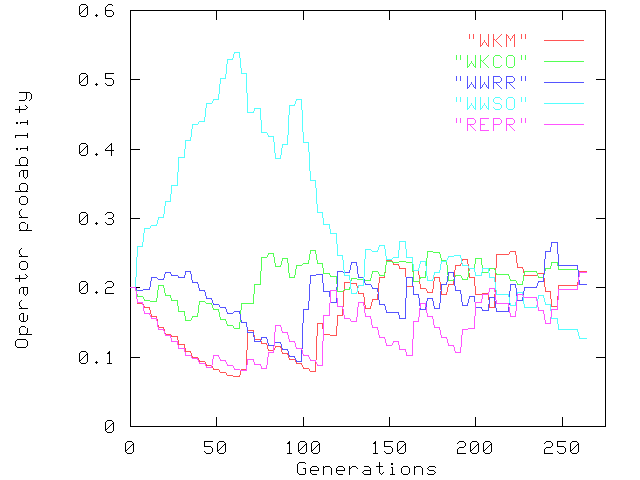Figure 4

Figure 4. Operator probabilities for GA5

For GA1 (Fig. 1), the effect of the adaptation algorithm can be clearly seen. For example, the early productivity of the heuristic path shift-out operator, WWSO, results in its probability rising from 0.2 to nearly 0.6 in the first 50 generations, although it subsequently reduces to below 0.2. In contrast, the far simpler path mutation, WKM, falls from 0.2 to below 0.1 before generation 50, only then to rise to over 0.3 due to higher productivity in the latter part of the run.

Comparing GA1 and GA3, the impact of the higher adaptation proportion ($\psi$) in the latter is obvious in the greater variability of the probability curves (Fig. 2). A similar effect is also apparent in Fig. 3, where in GA4 setting the credit constant ($\kappa$) to 0.0 resulted in wide fluctuations of operator probability, due to the hybrid's exclusive focus on operators producing direct improvements in fitness. In contrast, for GA5 (Fig. 4), although there is some initial variation of probabilities, particularly for the productive path shift-out operator (WWSO), after 120 generations all the operators settle to an approximately equal share of probability. This would seem to indicate that with grandparent and parent operators receiving equal credit ($\kappa = 1.0$), the algorithm is unable to respond to all but the widest differences in relative productivity.

Statistical comparison of the quality of results from the five hybrids is given in Tables 2 and 3. These record the best and median results at both the end (100,000 trials) and the early part (25,000 trials) of ten runs on all three networks. In each table, the best result for a given network is displayed in bold. In addition, as the same random seeds were used for each set of runs on a network, the sign test could be applied to matched pairs [12] from different hybrids to establish if there were significant differences in their medians. The resulting significance levels are included in the tables, with e.g. $s_{21}$ representing the significance level of the comparison of GA2 with GA1. Where a sufficiently low significance level for identical medians was obtained (i.e. in Table 2 at 25,000 trials), the best median for each network is also displayed in bold.

Table 2. Results with adaptation proportion $\psi$ = 0.00, 0.15 and 0.30 for ten runs
GA2 GA1 GA3 Significance Level
Network $\psi = 0.00$ $\psi = 0.15$ $\psi = 0.30$ (%)
Best Median Best Median Best Median $s_{21}$ $s_{13}$ $s_{23}$
$\times10^{6}$ $\times10^{6}$ $\times10^{6}$ $\times10^{6}$ $\times10^{6}$ $\times10^{6}$
100,000 trials
1 5.621 5.681 5.582 5.659 5.609 5.658 --- --- ---
3 4.861 4.917 4.879 4.945 4.833 4.924 --- --- ---
5 5.063 5.171 5.081 5.144 5.090 5.140 --- --- ---
25,000 trials
1 6.527 6.680 6.222 6.517 6.306 6.558 1.1 --- 5.5
3 5.642 & 5.722 5.468 5.604 5.535 5.739 0.1 5.5 ---
5 5.922 6.070 5.869 5.967 5.784 6.038 1.1 --- 5.5
Table 2. Results with credit constant $\kappa$ = 0.0, 0.5 and 1.0 for ten runs
GA4 GA1 GA5 Significance Level
Network $\kappa = 0.0$ $\kappa = 0.5$ $\kappa = 1.0$ (%)
Best Median Best Median Best Median $s_{41}$ $s_{15}$ $s_{45}$
$\times10^{6}$ $\times10^{6}$ $\times10^{6}$ $\times10^{6}$ $\times10^{6}$ $\times10^{6}$
100,000 trials
1 5.613 5.659 5.582 5.659 5.445 5.635 --- --- 5.5
3 4.887 4.932 4.879 4.945 4.875 4.928 --- --- ---
5 5.079 5.158 5.081 5.144 5.079 5.145 --- --- ---
25,000 trials
1 6.331 6.520 6.222 6.517 6.222 6.476 --- --- ---
3 5.460 5.610 5.468 5.604 5.545 5.631 --- --- ---
5 5.875 6.026 5.869 5.967 5.819 5.998 --- --- ---

Surprisingly, Table 2 at 100,000 trials shows that despite the wide differences in dynamic behaviour observed on individual runs, and discussed above, the final quality of results is unaffected by the choice of adaptation proportion ($\psi$). However, this can perhaps best be explained by also considering the relative performance in the early part of the same runs. The best results at this stage were achieved, as expected, by GA1 ($\psi = 0.15$), both in comparison with GA2 ($\psi = 0.00$; highly significant median differences) and GA3 ($\psi = 0.30$; significant median differences). It would appear, therefore, that although at 25,000 trials, GA1 is out-performing the other two, by 100,000 trials the productivity of the combination of problem-specific operators used is such as to allow both GA2 (fixed probabilities) and GA3 (high adaptation rate) to obtain final results of equal quality to GA1.

Different values of credit constant ($\kappa$) also produced much less dramatic variations in solution quality than expected. Table 3 records that at the end of the runs, the best results were obtained by GA5 ($\kappa = 1.0$). However, there was little significant difference in medians, with only some indication that GA5 ($\kappa = 1.0$) was better than GA4 ($\kappa = 0.0$). Evidence from the early part of the runs is inconclusive, indicating little effect by the credit constant on the initial quality of results. Taking account of the final results though, there is nevertheless some indication both that crediting parent and grandparent operators is to be preferred over simply rewarding the operator responsible for an improvement, and also that a higher credit constant than the usual $\kappa = 0.5$ may be beneficial.

Conclusions & further work

An investigation into the use of operator-probability adaptation in a genetic-algorithm/heuristic hybrid for minimum cost routing and wavelength allocation of multi-wavelength all-optical transport networks has been described. The experimental results indicate that in this application, with powerful problem-specific operators, the main benefits of operator-probability adaptation are in relieving the experimenter of the burden of setting initial probabilities and in the early performance of the hybrid, rather than in improvements of the final solution quality obtained. It is anticipated that future work will also explore the effectiveness of the operator-probability adaptation algorithm with a wider range of heuristic operators for wavelength allocation, as well as in other areas, such as virtual topology design. In addition, other measures of productivity could be examined, such as rewarding operators for improvements over either the median population fitness (at the end of the previous generation) [7] or their parents' fitness [8], rather than just over the best individual found.

Acknowledgements

The author is grateful to Prof. Rob Massara for his guidance of my Ph.D. project, and to Katerina Proestaki and Noel Parnis (all three from E.S.E., University of Essex) for many interesting discussions during the continuing development of NOMaD.

References

  1. M.C. Sinclair. NOMaD: Initial architecture of an optical network optimisation, modelling and design tool, Proc. 12th UK Performance Engineering Workshop, University of Edinburgh, UK, 157-167, Sep 1996.

  2. M.C. Sinclair. NOMaD: Applying a genetic-algorithm/heuristic hybrid approach to optical network topology design, Proc. Intl. Conf. on Artificial Neural Networks and Genetic Algorithms (ICANNGA'97), Norwich, UK, 301-305, Apr 1997.

  3. M.C. Sinclair. Minimum cost routing and wavelength allocation using a genetic-algorithm/heuristic hybrid approach, Proc. Sixth IEE Conf. on Telecommunications, Heriot-Watt University, Edinburgh, UK, Mar/Apr 1998.

  4. A.L. Tuson. Adapting Operator Probabilities in Genetic Algorithms, M.Sc. thesis, Dept. of Artificial Intelligence, University of Edinburgh, UK, 1995.

  5. A. Tuson & P. Ross. Co-evolution of operator settings in genetic algorithms, AISB Workshop on Evolutionary Computation, 1996.

  6. L. Davis. Handbook of Genetic Algorithms, Van Nostrand Reinhold, 1991.

  7. B.A. Julstrom. What have you done for me lately? Adapting operator probabilities in a steady-state genetic algorithm, Proc. Sixth Intl. Conf. on Genetic Algorithms, University of Pittsburgh, USA, 81-87, Jul 1995.

  8. A. Tuson & P. Ross. Cost based operator rate adaptation: An investigation, Proc. Fourth Intl. Conf. on Parallel Problem Solving From Nature (PPSN IV), 1996.

  9. R. Hinterding, Z. Michalewicz & A.E. Eiben. Adaptation in evolutionary computation: A survey, Proc. 1997 IEEE Intl. Conf. on Evolutionary Computation (ICEC'97), Indianapolis, Indiana, USA, 65-69, Apr 1997.

  10. N. Wauters & P. Demeester. Design of the optical-path layer in multiwavelength cross-connected networks, IEEE J. Select. Areas Commun., 14(5):881-892, Jun 1996.

  11. P.S. Griffith, A. Proestaki & M.C. Sinclair. Heuristic topological design of low-cost optical telecommunication networks, Proc. 12th UK Performance Engineering Workshop, University of Edinburgh, UK, 129-140, Sep 1996.

  12. P. Sprent. Applied Nonparametric Statistical Methods, Chapman & Hall, 1989.

Please feel free to comment on this page.
Creator: Mark C Sinclair <mcs@ieee.org>
Date: 14 vi 1999
[Home] [Research] [NOMaD] [ETBib] [Publications] [Students] [Links] [CV]
1