費波拿契數列中的素數

意大利數學家費波拿契 (Leonardo Pisano Fibonacci 約1170 - 約1250)

(照片取自「The MacTutor History of Mathematics Achieve」http://www-gap.dcs.st-and.ac.uk/~history/ )

 

費波拿契數列

所謂費波拿契數列 (Fibonacci Sequence) 簡稱 Fn，即 1, 1, 2, 3, 5, 8, 13, 21,... (OEIS A000045)

當中 F1 = F2 = 1，Fn+2 = Fn+1 + Fn (其中 n = 1,2,3,...)

我們也可定義 F0 = 0 。

當中的數便是費波拿契數 (Fibonacci Number)。

它是 13世紀意大利數學家費波拿契 (Leonardo Pisano Fibonacci 約1170-約1250) 研究一有趣的問題而產生，故以之為名。

什麼有趣的問題啊？

設每一對兔子每月會產下一對小兔，小兔一個月後會長大變成大兔。如果沒有死亡，問由一對大兔開始，一年後有多少對大兔呢？

我們不妨設開始時大兔的對數為 F1 ，一個月後的大兔的對數為 F2，兩個月後的大兔的對數為 F3，一般地 n 個月後的大兔的對數為 Fn+1 。

由題可知 F1 = 1，一個月後，牠們了生了一對小兔，但大兔的對數仍為 1，即 F2 = 1。再過了一個月，小兔長大了，大兔又生了一對小兔，大兔的對數成了 2 ，即 F3 = 2 。如此下起，我們有 F4 = 3 、 F5 = 5 、 F6 = 8 ....

一般的，第 n+1 個月以後的大兔對數是包含了兩個部份：一是原本第 n 個月以後的大兔對數，二上個月的小兔對數，因牠們成長了，成了大兔，這實是第 n-1 個月以後的大兔對數。故有 Fn+2 = Fn+1 + Fn 。

這數列 Fn 便是我們現在所言及的費波拿契數列。回到問題，一年以後，即 12 個月以後，即 F13 = 233 便是我們耍的答案了。

其實費波拿契數有很多特別的地方：

F1 + F2 + F3 +...+ Fn = Fn+2 -1

F2 + F4 + F6 +...+ F2n = F2n+1 -1

F1 + F3 + F5 +...+ F2n-1 = F2n

F12 + F22 + F32 +...+ Fn2 = Fn Fn+1

Fn+12 = FnFn+2 + (-1)n

F2n = Fn+12 - Fn-12

F3n = Fn+13 + Fn3 - Fn-13

 

當中亦有一些著名的恒等式 (Identity) 和費波拿契數相關：

Fn2 - Fn+rFn-r = (-1)n-rFr2 (卡塔蘭恒等式 Catalan's Identity)

FmFn+1 - Fnm+1 = (-1)nFn+m (迪奧卡尼恒等式 d'Ocagne's Identity)

Fn4 - Fn-2Fn-1Fn+1Fn+2 = 1 (格林 - 切薩羅恒等式 Gelin - Cesaro's Identity)

Fn-1Fn+1 - Fn2 = (-1)n (卡西尼恒等式 Cassini's Identity)

 

我們亦可以下式計出費波拿契數的值：

 

費波拿契數列的生成函數 (Generating Function) 為：

 

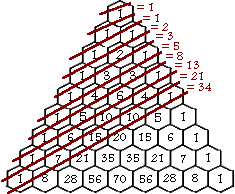
我們亦可從柏斯卡三角形 (Pascal's Triangle) 中找到費波拿契數列：

 

費波拿契素數

而我們有興趣是當中出現的素數：F3=2 、 F4=3 、 F5=5 、 F7=13 、 F11=89 、 F13=233 、 F17=1597 、F23=28657 、 F29=514229 、 ... 我們稱這些素數為費波拿契素數 (Fibonacci Prime)。 (OEIS A005478 及 A001605)

下表列出十大費波拿契素數：

n
數位
發現者
年份
81839
17103
禾達 (Bouk de Water) / 布靴斯特 (David Broadhurst)
2001
50833
10624
歐文 (Sean A. Irvine) / 布靴斯特 (David Broadhurst) /
禾達 (Bouk de Water) / 倫斯 (John Renze)
2005
37511
7839
倫斯 (John Renze)
2005
35999
7523
禾達 (Bouk de Water) / 布靴斯特 (David Broadhurst)
2001
30757
6428
禾達 (Bouk de Water) / 布靴斯特 (David Broadhurst)
2001
25561
5342
禾達 (Bouk de Water) / 布靴斯特 (David Broadhurst)
2001
14431
3016
禾達 (Bouk de Water) / 布靴斯特 (David Broadhurst)
2001
9677
2023
禾達 (Bouk de Water)
2000
9311
1946
都伯納 (Harvey Dubner) / 凱勒 (Wilfrid Keller)
1995
5387
1126
莫蘭 (Francois Morain) / 威廉士 (Hugh C. Williams)
1990

若我們考慮的是擬素數 (Probable Prime)，即那些通過費馬小定理的逆命題 (Converse of Fermat's Little Theorem) 來測試的數，這有很大機會是素數，或可能是卡邁克爾數 (Carmichael Number)。那我們可把 n 推至 433781。但正因為 n 很大，要判斷該數的素性的確不易。

我們不難發現除了 F4 = 3 以外，其餘的第 p 個費波拿契數 ( p 是素數) Fp 也是素數。原來所有費波拿契素數，除了 F4 = 3 以外，都有一素次數。但反之則未必成立，如 F19 = 4181 = 37 * 113、 F31 = 1346269 = 557 * 2417 ：即不是所有有素次數的費波拿契數也是素數。故是否有無限多個費波拿契素數也是未知之事，但數學家們傾向認為這存有無限多個費波拿契素數。

 

參考文獻及網址：

Caldwell, C. K. "The Top Twenty: Fibonacci Number." http://primes.utm.edu/top20/page.php?id=39.

Gardner, M. Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments from Scientific American. New York: Knopf, 1979.

Weisstein, E. W. "Fibonacci Number." From MathWorld. http://mathworld.wolfram.com/FibonacciNumber.html.

 

1