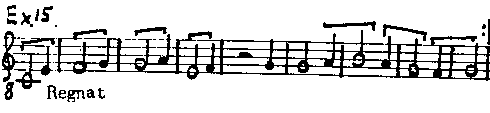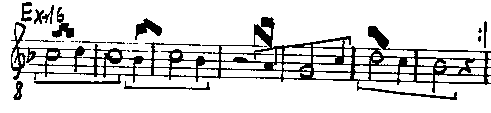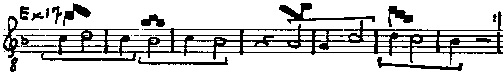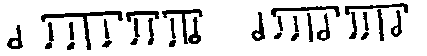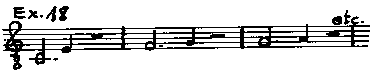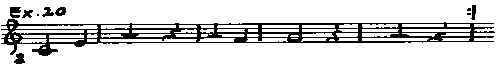39
ligated. The two ligated notes with the brevis and longa following
could be ligated and they would be the equivalent of four ligated notes cum
proprietate and cum perfectione1. If there are three ligated
notes to one syllable cum proprietate and cum perfectione, if a
brevis longa follow, or if they are treated as an absolute, their quantity is shown,
since they are equal to a longa, brevis, longa, according to the rule, which
states: Every figure cum proprietate, etc.... If, however, the three
afore-mentioned ligated notes are sine perfectione, then they will be made
perfect by the following brevis and longa. In such a case, they will
form the equivalence of five ligated notes cum proprietate and cum
perfectione. Five notes, however, may be reduced to four, and four notes to three;
thus, all the notes, from the first to the last, will be equal in durational value to
three ligated notes cum proprietate and cum perfectione2.
Again, if two ligated notes to a syllable are formed sine
proprietate and cum perfectione, which, however, is not used too often, and
there is a longa to the following syllable, together they form the equivalence of
three ligated notes cum proprietate and cum perfectione. Again, if there
are two ligated notes sine proprietate and sine perfectione to one
syllable and the same to another syllable, and a longa to a further syllable,
they form the equivalence of three ligated notes cum proprietate and cum
perfectione, and of two notes cum proprietate and cum perfectione.
Thus, any one who knows the rules given above has all the information necessary to figure
these out, as shall be shown fully below3.
Coussemaker p. 343b19 to p. 344a5
1) It makes more sense to have the following
series of ligatures 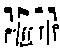 than
than 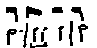 as suggested by Coussemaker,
since the first one fulfills the conditions more exactly, whereby the text syllables would
not extend over the perfection. Thus, if the four notes at the end were combined in one
ligature, they would be notated in the following fashion:
as suggested by Coussemaker,
since the first one fulfills the conditions more exactly, whereby the text syllables would
not extend over the perfection. Thus, if the four notes at the end were combined in one
ligature, they would be notated in the following fashion: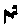 Actually, the initial longa could be
combined in one ligature, they would be notated in the following manner:
Actually, the initial longa could be
combined in one ligature, they would be notated in the following manner: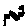 but since the first longa
would have three durational units, and since for our theorist the ligatures cum
proprietate are used for the beginning of the first mode, it would be ambiguous to
have included the first longa.
but since the first longa
would have three durational units, and since for our theorist the ligatures cum
proprietate are used for the beginning of the first mode, it would be ambiguous to
have included the first longa.
2) This would necessitate that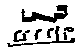 would become the equivalence of
would become the equivalence of 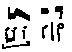 . If five notes are the
equivalence of three, then they would have to be cum opposita proprietate,
whereas four notes would be cum proprietats. In this regard, we again see that
the three-note ligature cum proprietate and cum perfectione is measured longa
brevis, longa according to this theorist.
. If five notes are the
equivalence of three, then they would have to be cum opposita proprietate,
whereas four notes would be cum proprietats. In this regard, we again see that
the three-note ligature cum proprietate and cum perfectione is measured longa
brevis, longa according to this theorist.
3) In the first case, our theorist evidently feels that a
three-note ligature cum proprietate and cum perfectione may equal three
consecutive longæ, as in the first ordo of the fifth mode, scilicet: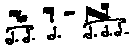 The second case is more
straightforward
The second case is more
straightforward 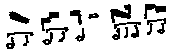 where
the three-note ligature still has the modal significance of an initial longa, whereas the
substitute form has been made mensural (id est, sine proprietate).
where
the three-note ligature still has the modal significance of an initial longa, whereas the
substitute form has been made mensural (id est, sine proprietate).
40
Thus, from what has been said, we gather that every
ligated figure containing more than three notes, or two ligated and one, or one and two
ligated, can be related to a form having three ligated notes. As far as those which are
said to be cum proprietate and sine perfectione are concerned, initially
there were many different ways of notating them. They were treated, however, in an
ambiguous manner, since there was no real way of notating them1. In the older
books there was an exceedingly large number of ambiguous note-forms, since all of the notæ
simplices had the same form. The musicians at this time could only reason things out,
saying: I know this note to be a longa, this one to be a brevis. They
suffered under this for an exceedingly long time before they knew that which we all know
and which, by means of what has just been stated, makes all of the difficulties inherent
in notational problems simple of solution. Thus, one progresses more in one hour in this
fashion, than in seven previous.
Concerning what we have just discussed, the greater part of
the knowledge of the ancients did not take into consideration the formal shapes of notes.
They had based their knowledge of consonances on entire melodies, especially on the
octave, fifth and fourth. More information about these intervals will be given below in
the fourth and fifth chapters of this treatise. Accordingly, the upper-voice respected the
lower-voices. These persons taught others, saying: Listen to them and be guided by them
while singing. They had, however, few distinct notational forms, and they said: The
upper-voice must form a good consonance with the lower-part, and that is enough. This was
the way they stated the problem for a long time, before they began to teach.
The notational symbols were codified about the time of
Perotinus the Great, and a little before him, and they were taught in a more abbreviated
fashion. After this, there was Master Robert de Sabilone, although he taught rather
extensively, but he made the vocal melodies too pretentious.
For this reason, a notable Parisian, Master Petrus Trothun,
Aurelianus, concerned himself with plain chant. nevertheless, he knew too little, as was
rumored, about durational values. These were matters, however, which the afore-mentioned
Master Robert knew intimately and was able to teach well.
After this, there was Master Petrus, the greatest notator,
who followed these teachings, and who notated his books in a manner which was exceedingly
faithful to the uses and habits of his master.
At this time, there was a person, who was called Thomas de
Sancto Iuliano, an old Parisian; he did not notate according to the method of the others,
but followed closely the method of the older notators.
There was also another Englishman, and he followed the
English method of notating, and he taught there also.
Coussemaker p. 344a6 to p. 344b15
1) This ligature is only really important in
compositions with rhythmic text. 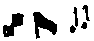 or
or 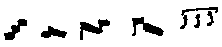 For the
ambiguities of form in this ligature in the Montpellier manuscript (H 196),
confer my article in Musica Disciplina IX 1955.
For the
ambiguities of form in this ligature in the Montpellier manuscript (H 196),
confer my article in Musica Disciplina IX 1955.
41
A certain Iohannes, mentioned above, continued all of the
methods of notation alluded to above after these theorists and during his own life time
and until the time of, Master France, with other masters, such as Master Theobaldus
Gallicus, and Master Simon de Sacalia, a certain Master (Iohannes) de Burgundia, and a
certain honourable gentleman from the Picardy, whose name was Iohannes le Fauconer.
There were good singers in England, and they sang
beautifully, like Master Iohannes filius Dei1, or like Makeblith in Winchester
at the imperial court of King Henry the Last2. There was also another good
singer of many different kinds of songs and polyphonic compositions and other types of
music. We shall have cause to mention these other kinds below, etc.
Again, two ligated notes cum proprietate and sine
perfectione above one syllable with a longa following, may be related to
three ligated notes cum proprietate and cum perfectione, or if a brevis
and a longa follow, they may be reduced to three, in a similar manner3.
In a similar fashion, we can conceive of four, five and six
notes, cum proprietate and sine perfectione, with a following longa
above one syllable, as being related to three ligated notes. In the books of certain of
the older writers, no such significance was paid to the notational forms. They were able
to proceed only according to their understanding, always using forms which were cum
proprietate and cum perfectione. Such notation is found in the books of the
Spanish and the Pamplonians, as well as in the books of the English; there were different
gradations of this, sometimes more (attention was paid to notational devices), sometimes
less.
The French, or the Parisians, had all of the above mentioned
methods annotating, as is shown in different books by different notators. In the
following, we shall concern ourselves with the methods of evaluating these.
The first mode utilized note forms as in the first chapter
in this fashion: three ligated notes cum proprietate and cum perfectione,
after this two ligated notes cum proprietate and cum perfectione, and in
a similar manner two, two, two ligated notes, to as great an extent as desired. The
principle underlying this mode is treated below.
Again, the first ordo of this mode consists of
three ligated notes cum proprietate and cum perfectione, with a brevis
rest, etc.
Coussemaker p. 344b16 to p. 345a23
1) Ludwig (Archiv für Musikwissenschaft, V
1923 p. 315) draws attention to the fact that W. Dugdale (The History of St. Paul's
Cathedral in London, 1658 p. 220) lists the presentation in 1295 of a good proper to the
library of St. Paul's Cathedral by a Iohannes filius Dei.
2) Identified by J. Wolf, Geschichte der Mensuralnotation, I, p.
15-16 as Henry III (1216-72). This note is important for dating this treatise, since, as
Wolf points out Henricus ultimus probably refers to the fact that the king has
just recently died, which makes the date of this treatise as circa 1275.
3)  or
or 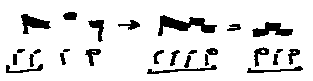 . The following paragraph is repetitious in Coussemaker's text and is
omitted.
. The following paragraph is repetitious in Coussemaker's text and is
omitted.
42
The second ordo adds two ligated notes cum
proprietate and cum perfectione to the first ordo. The third ordo
adds two notes to the second, in a similar manner. The fourth ordo similarly adds
two notes to the third, and this may be continued as far as one wishes, whereby the rule
follows: There will always be one more group of two ligated notes after the three, always cum
proprietate and cum perfectione, than the number of the ordo.
Because the ordo must always involve an increase by two ligated notes, you will
find that a single note can not be added, since this is not used; however, one note added
to three notes is in use, at least among those persons who do such things1.
The principle underlying the second mode is realized in the
following notational manner: two, two, two etc. ligated notes cum proprietate and
cum perfectione, with three notes at the end sine proprietate and cum
perfectione. The first ordo of this mode is notated in the following
fashion: three ligated notes sine proprietate and cum perfectione, with
a longa rest of two durational units, etc. This may be repeated as often as one
wishes. The second ordo is formed with two ligated notes cum proprietate
and cum perfectione, and three notes sine proprietate and cum
perfectione, with a longa rest of two durational units. The third ordo
increases the second ordo by two ligated notes. These are added at the beginning
and not at the end of the ordo. In the case of the first mode, as mentioned
above, the notes were added at the end of the ordo, and not at the beginning,
that is after the three and two notes. Thus, in the second mode, the fourth ordo
adds two ligated notes before the third ordo. You can check practical examples by
these rules to see what the principle of notation is, as was done with the chorale
fragment Latus above. In this fashion, we are able to understand the perfect
modes.
The principle underlying the first imperfect mode can be
realized in two notational manners. The first method proceeds like the first perfect mode,
namely: three, two, two, two etc. ligated notes all cum proprietate and cum
perfectione; at the end, however, a single brevis is added, which makes the
mode imperfect. Others say that the second method of notating is better, namely: two, two,
two, two etc. ligated notes all sine proprietate and cum perfectione;
thus, there will never be a single note alone at the end, since one of their rules is:
Nothing must be written disjunctly, that can be ligated. There is, however, another rule
which is in opposition to this one, namely: that you must not notate sine proprietate,
if you can notate cum proprietate; and that nothing must be made sine
perfectione, which may be fashioned cum proprietate. That which expresses
one's meaning best, however, should be used. The first ordo of the first
imperfect mode is realized in the following manner: two ligated notes sine proprietate
and sine perfectione followed by a longa rest of two durational
units; then, two ligated notes cum proprietate and cum perfectione and a
brevis rest of one durational unit. This is the best known ordo, but is
seldom used; and this may be repeated over and over again, as often as you wish.
Coussemaker p. 345a24 to p. 345b33
43
The second ordo adds two ligated notes similar
to the first ones (id est, sine proprietate and sine perfectione) for
the first group and two notes similar to the second ones (id est, cum proprietate and
cum perfectione) for the second group; the rests consist of a longa for
the first group, and a brevis for the second. The third ordo adds two
ligated notes similar to the first group to the second ordo, and two ligated
notes similar to the second group. The fourth ordo adds two ligated notes to the
third ordo, and two ligated notes to the second part, as stated above.
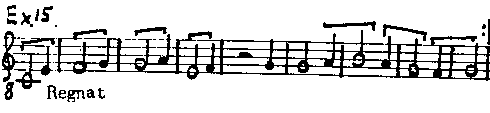
The principle of notation may also be realized in the
following manner: three ligated notes cum proprietate and cum perfectione
followed by three ligated notes sine proprietate and sine perfectione, etc.
Others, however, don't consider this to be proper, as stated above, whereby it is not used
except in a certain type of song, as shall be aptly demonstrated below, as well as above
in the examples using Latus.
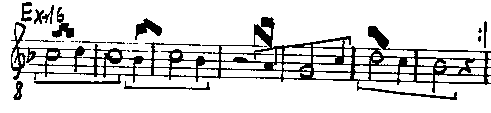
The principle underlying the second
imperfect mode is realized in the following manner: two, two, two etc. ligated notes
always cum proprietate and cum perfectione. Another form of this mode
has three ligated notes sine proprietate and cum perfectione, and three cum
proprietate and cum perfectione, etc. This is, however, not used, as also
was said concerning the similar form of the opposite, first mode.
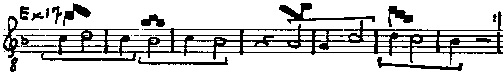
The first ordo of this is formed in the
following manner: two ligated notes cum proprietate and cum perfectione in
form, although actually to be understood as being sine perfectione (id est, really
because the perfection is not complete) followed by a brevis rest of one
durational unit which completes the perfection of the previous note1;
Coussemaker p. 345b34 to p. 346a21
1) The point is not that the previous note of
two durational units and the following brevis rest form a perfection
43
The second ordo adds two ligated notes similar
to the first ones (id est, sine proprietate and sine perfectione) for
the first group and two notes similar to the second ones (id est, cum proprietate and
cum perfectione) for the second group; the rests consist of a longa for
the first group, and a brevis for the second. The third ordo adds two
ligated notes similar to the first group to the second ordo, and two ligated
notes similar to the second group. The fourth ordo adds two ligated notes to the
third ordo, and two ligated notes to the second part, as stated above.
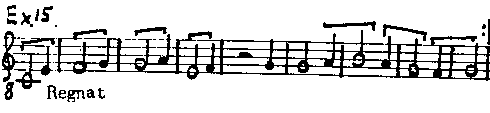
The principle of notation may also be realized in the
following manner: three ligated notes cum proprietate and cum perfectione
followed by three ligated notes sine proprietate and sine perfectione, etc.
Others, however, don't consider this to be proper, as stated above, whereby it is not used
except in a certain type of song, as shall be aptly demonstrated below, as well as above
in the examples using Latus.
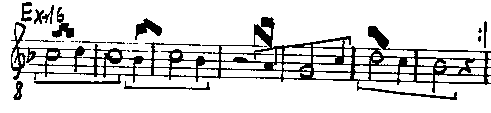
The principle underlying the second
imperfect mode is realized in the following manner: two, two, two etc. ligated notes
always cum proprietate and cum perfectione. Another form of this mode
has three ligated notes sine proprietate and cum perfectione, and three cum
proprietate and cum perfectione, etc. This is, however, not used, as also
was said concerning the similar form of the opposite, first mode.
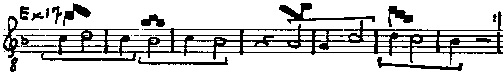
The first ordo of this is formed in the
following manner: two ligated notes cum proprietate and cum perfectione in
form, although actually to be understood as being sine perfectione (id est, really
because the perfection is not complete) followed by a brevis rest of one
durational unit which completes the perfection of the previous note1; after
this, there are two
Coussemaker p. 345b34 to p. 346a21
1) The point is not that the previous note of
two durational units and the following brevis rest form a perfection but rather
that the group is conceived of as a ligature of three notes. 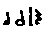 The two-note ligature is perfect in form,
accordingly, but to be conceived as imperfect, since it is only completed by the final
note, in this case a rest.
The two-note ligature is perfect in form,
accordingly, but to be conceived as imperfect, since it is only completed by the final
note, in this case a rest.
44
ligated notes cum proprietate and sine perfectione in form, followed
by a longa, or two ligated notes cum proprietate and cum perfectione
in form, but not understood as such. Actually, they are understood as being sine
perfectione and the perfection (of this ligature) is completed by the longa
rest which follows, etc. Fashion all of the ordines of this imperfect mode in a
similar manner, in the same way as stated above for the first imperfect mode. The
propriety and the perfection of this mode, however, will be just the opposite as for that
mode, etc. According to this last rule, and with the help of consonances, you will be able
to solve the greater part of the ambiguous places in the books of our predecessors. This
is possible either when text is present, or when there is none if repeated notes should
cause the ligature to be broken up, etc. Because of this, it is not necessary in such
sciences always to hold completely to the precise propriety and perfection, but the result
is always better and the music can be presented better and in a more compact manner, as
shall be sufficiently demonstrated below.
The principle underlying the third perfect mode is realized
in the following manner: a longa, three, three, three etc. ligated notes cum
proprietate and cum perfectione, with a longa rest of three
durational units.
The first ordo of the third perfect mode is formed
in the following manner: a longa and three ligated notes, with a longa
rest of three durational units, etc.
The second ordo adds (three ligated notes) to the
first ordo.
The third ordo adds three ligated notes to the
second ordo.
The fourth ordo adds three ligated notes to
the third ordo, and these groups are always cum proprietate and cum
perfectione, and are followed by a longa rest. Whereby it follows that of
the three ligated notes after the longa, the first two are breves. The
English sing in this irregular mode. They speak of this mode as consisting of two ligated
notes and a brevis, etc. Quite often the brevis is equal in durational
value to the two ligated notes, and quite often it is not1.
The principle underlying the fourth perfect mode is realized
in the following manner: three, three, three etc. ligated notes cum proprietate
and cum perfectione, with two ligated notes sine perfectione at the end.
It is intended that the perfection of these two ligated notes be completed in the
longa rest, although the rest can not be counted, as is often shown2, when
the first longa of the third mode and one at the end have been removed.
Coussemaker p. 346a21 to p. 34622
1) This may be a reference to a binary version
of the third mode as practiced in England and elsewhere, confer my Binary Rhythm,
Musical Theory and the Worcester Fragments, in Musica Disciplina, VII 1953
p. 48, footnote 7.
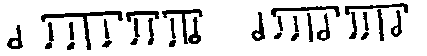
2) The difference between the third and fourth modes is that in
the third [Continuation of text, confer p. 73]
45
The first ordo of the fourth perfect mode is
formed in the following way: three ligated notes cum proprietate and cum
perfectione and two cum proprietate and sine perfectione, followed
by a longa rest.
The second ordo adds three ligated notes cum
proprietate and cum perfectione ahead of the two ligated notes cum
proprietate and sine perfectione; this then is followed by a longa
rest.
The third ordo similarly adds three ligated notes
to these.
The fourth ordo similarly adds three ligated notes
to these.
The principle underlying the third imperfect mode is
realized in the following manner: a longa, three, three, three etc. ligated notes
always cum proprietate and cum perfectione, followed by two ligated
notes cum proprietate and sine perfectione, etc. The first ordo
of the third imperfect mode which has been reduced by one note from its perfect form, is
realized in the following manner: Remove the last note from the ligature of three notes,
no matter how it was notated, and retain the rest, letting them be formed as a longa and
two ligated notes cum proprietate and sine perfectione, or understood as
such, or both, and followed by a longa rest. In this way, we can derive the first
ordo of the third imperfect mode from the first ordo of the third perfect
mode. In the same fashion, we can derive the second ordo of the third perfect
mode from the second ordo of the third perfect mode, and the third ordo
from the third, and the same is true for all ordines.
Again, there is the first ordo of the third
imperfect mode which is reduced by two notes from its perfect form, or by one note from
the first ordo of the third imperfect mode as depicted above; this is notated in
the following manner: a longa and a brevis with a brevis rest
of two durational units.
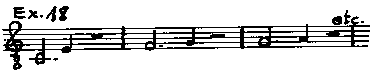
It is to be noted, that it is not possible to shorten the
other imperfect modes mentioned above. For the continuation of the mode which was
mentioned above (id est, the third imperfect mode reduced by one note from its
perfect form), after the longa and the two breves with a longa
rest, put three ligated notes cum proprietate and cum perfectione,
followed by a longa rest which is equal to the two breves. Thus, you
will be able to distinguish the above-mentioned modes from all of the other imperfect
ones. The individual ordines have thus been exemplified adequately with the
consideration of this one mode, as explained more fully in the first chapter.

Coussemaker p. 346b23 to p. 347a23
46
The principle underlying the fifth perfect mode is
realized in longæ which are not ligated, and which have no rests in any position
corresponding to an odd number of notes. The first ordo of this mode is found in
two different ways both in older and more recent books; the one method uses three longæ
not ligated followed by a longa rest, etc. There will always be three, that is an
uneven number of notes. The other way is to have three ligated notes cum proprietate
and cum perfectione, and a longa rest of three durational units, and
then three and three more ligated notes, etc. Actually, these ligatures are not exactly
proper, when one takes into account all that we have stated. This notational device is
used, however, in the tenores of descants or motets, because of the excellence of notation
and according to the following rule: Whatever can be ligated, should not be written
disjunctly. In other ordines of this mode, however, the notes are never ligated,
but are always written disjunctly. This mode always involves odd numbers of notes, so that
the second ordo consists of five longæ all disjunct with a longa rest.
Similarly, the third ordo consists of seven longæ all disjunct, with a longa
rest, etc.
The principle underlying the sixth mode is realized in two
ways, according to whether the mode is reducible to the first or to the second mode. If
the sixth is reducible to the second mode, the following pattern is realized: two ligated
notes cum proprietate and cum perfectione with a stem (plica) at
the end drawn either upwards or downwards, and two more ligated notes with a stem, and two
with a stem etc. without any rest. There will be a single brevis at the end to
make the mode perfect, since without this the series would exemplify the principle of the
imperfect mode, and it would become the sixth imperfect mode. If, however, the sixth mode
is reducible to the first, one proceeds as follows: four ligated notes cum proprietate
and cum perfectione with a stem drawn either upwards or downwards, then two
ligated notes cum proprietate and cum perfectione with a stem, and two
ligated notes with a stem, two, two, two etc. without a rest etc.
This stem, however, quite often fools performers because
they don't know how far to go up or down, unless they are excellent musicians.
Accordingly, others have used four ligated notes at the beginning without a stem, and
after that three and three and three ligated notes, all cum proprietate and cum
perfectione. They are able to recognize the sixth mode by this pattern, and this is
easily seen in the Alleluia Vs Posui adiutorium1 after the
first longa rest. Others will speak of the passage after the first clausula,
which still others call a period, using the language of instrumentalists; they say, that
this is sufficiently the first period.
Another such passage is offered in the second period (clausula)
2, of this Alleluia etc., accordingly, we can proceed with the
discussion of its ordines.
Coussemaker p. 347a24 to p. 347b35
1) Reference is made to M 51, most easily
available in transcription in Y. Rokseth, Polyphonies du 13e siècle,
II 1936 p. 31ff. measures 9ff. Garlandia, Coussemaker p. 180, also makes
reference to this passage, although the example is corrupt, and is better in Cserba
p. 202 and Coussemaker p. 101.
2) Probably, reference is being made to measures 13-19 which
repeats some of the melodic material of measures 9-12. Otherwise, the composition does not
appear to contain a comparable passage.
47
The first ordo is formed in the following
manner: four ligated notes cum proprietate and cum perfectione etc. The
final note can be conceived of in two different ways; either it is a longa or a brevis.
If t is a longa, then it is equal to two breves. If this is the
case, then the first three notes take the place of a longa and a brevis
and then the longa with a brevis rest constitutes the second perfection,
etc. This may then be continued. This method of notating can be increased or decreased by
diminution in the same manner as the third mode above, but in this case, the first note is
always ligated, whereas it had been disjunct before.
Another form is to have four ligated notes sine
proprietate and cum perfectione with a longa rest of two durational
units, if the mode is reducible to the second1. Or you could have two ligated
notes cum proprietate and cum perfectione with a stem (plica),
and a single brevis. This form of the mode is worse than the other, although
sometimes it is better or about the same, as for example whenever there are repeated
tones. This will suffice for the present in this second chapter for the understanding of
that which follows, as stated above.
Chapter III
Concerning Rests
The third chapter of this treatise concerns itself with
the kinds and durational values of rests. A rest is a pause or omission of sound for a
definite length of time or durational units, and has either the value of a longa
or a brevis according to its use in the six afore-mentioned modes. There are many
kinds of rests. One kind is a single rest, another a double, another a triple and another
a manifold rest. A single rest is one, which has the durational value of a single
longa or a single brevis of any of the afore-mentioned modes. The durational
value is measured with consideration to the succession of longæ and breves
immediately preceding the rest, according to the ordo, as exempli gratia
the first or second mode etc. If the first perfect mode is used in ligated form
immediately before the rest, the rest will be a single brevis rest of one
durational unit. The afore-mentioned mode will continue anew after this rest. If the same
mode is followed both before and after the rest, whether this be perfect or imperfect, the
rest is considered perfect in its own right.
The rule follows: Every rest of the first or second mode,
etc., if the same mode is used both before and after the rest, is or may be considered to
be a perfect rest. Thus, the afore-mentioned rest is perfect because of the manner of its
employment. We would say the same thing, if the rest had the durational value of a longa
of two durational units in either the first or second modes. In such a case, the note just
preceding could be a brevis, as also the following one in the continuation after
the break, etc. This would be true, even if the first imperfect mode preceded the rest and
the second perfect or imperfect mode followed, for example.
Coussemaker p. 347b36 to p. 348b11
1) The use of this ligature is analogous to its
use in the second mode, which is formed with three ligated notes sine proprietate
and cum perfectione.
48
Let us return to the first ordo of the first
mode, as exemplified by the tenor Latus. This example was also shown above with
all the perfect ordines in the second or opposite mode, or was offered fully in
all the perfect and imperfect forms of this mode. The largest rest possible will have the
durational value of a brevis, when a longa both precedes and follows in
the first mode. This is so, because every regulative rest continues the preceding mode;
after the following section, it may be used again with the same excellent results, etc.
It should be noted that there are two kinds of rests. There
is one kind which separates the different modes from each other. The other kind unites
them, and does not separate modes, whereby the same mode continues both before and after
the rest. Thus, this latter rest does not separate the modes except for the duration of
the rest. Thus, there can be a longa or a brevis in the first perfect or
imperfect mode, or in the second perfect or imperfect mode. As far as the sixth mode is
concerned, it can either be considered by itself, or as reducible to the first or second
mode. Rests also fit very well into the third mode, where they can have the durational
value of one, two or three units; similarly in the fourth mode. In the fifth mode, rests
will have the durational value of three units. In this mode, the rests will only have
different values if one of the modes (id est, rhythmic values) is split either in
its own right, or for the purpose of introducing another mode, as stated above.
A double rest is one in which the single longa or brevis
rest has been doubled, tripled or quadrupled, etc. The last rest should properly be called
a manifold rest, and is used often to indicate a change of mode for a series of notes.
Thus, the durational value of the rest may be established
according to one method by equating the upper and lower voices. Alternatingly, they may be
established by the indicated length of the notational stems (id est, vertical
lines designating the extent of the rest), as may be seen in many older and more recent
books.
The first example is both conceived of and realized in the
same fashion. It is shown in the first ordo of the first perfect mode as follows:
longa brevis and longa are sung, and brevis, longa brevis are
rested; then, longa brevis, longa are again sung, and the pausing and singing
continue.
Thus, we have the rule: If the made is either perfect or
imperfect before the rest, and if it continues with the same note values as it had ended,
the rest will be perfect. If these note values, before and after the rest, are different,
then the rest will be imperfect and cause a different disposition of longæ and
breves.
Thus, if a perfect mode is used before the rest, and
the same mode is followed both before and after the rest, a double or a manifold rest will
also be perfect. If, however, there are different modes before and after, such as the
first mode before the rest and-the second mode thereafter, the rest is imperfect when
there is an even number of notes, and perfect when there is an odd number of notes or
durational values, taking into consideration the substitution of equivalent notes. The
reason for this is that every perfect mode must end with the same durational value as it
began. In the case where the two notes consist of a brevis and a longa,
such a group is ended by a durational value different from the one which began it. Thus,
an even number of notes, considered either below or above (id est, in the lower
or upper-voice), will result in an imperfect mode.
Coussemaker p. 348b12 to p. 349a33
49
Manifold rests are only found in the first and second
perfect or imperfect modes and in the sixth mode to the extent necessary. They fit better
into the third, fourth and fifth modes, where there are durational quantities of one, two
and three units. This is true whether the modes are used in their own right, or whether
they are reduced to any of the afore-mentioned modes. Sufficient examples of the fifth
mode can be shown that are perfect and imperfect, where double and manifold rests are used
following odd and even numbers of notes, as stated above. If, however, this mode is split
and is reduced to the first, second or sixth mode, other rests are found which are
understood universally, generally, specifically and individually according to their use in
their or dines as they shall be explained in notational symbols below.
An example of the first kind of single rest is offered by
the tenor Latus, where the rest is a brevis. Another example is found in the
above-mentioned second perfect mode in Latus, where the rest will be a longa
of two durational units. A rest of three durational units is found in the tenor Regnat
in the third perfect mode. It should be noted, that the notational symbol for a rest,
placed between two melodic passages of the same or different ordines, is called a
stem. There are many ways of indicating the precise nature of a rest. One way is to extend
a stem from one line to the next, or to cover the space in between two lines, which are
ruled in by notators of music.
Certain notators were accustomed to write music for plain
chant in between two lines of text, or above one line of text, and they ruled four lines
of the same colour. Older notators didn't follow this procedure, except when three of the
lines had different colours; others would use two colours, and still others would use only
one colour. The lines were ruled by a metal stick, as in the books of the Carthusians and
others. The books of the composers of polyphonic music in France, Spain, and Arragón, and
in parts of Pamplona and England and in many other places, did not follow this procedure,
as is clearly shown in these books. In stead, these notators used red or black inked lines
of one colour. At the beginning of each line, they put a clef on such notes as C, F, or G
or other convenient places. Certain of the older writers, however, used different
placements of a square to indicate the signature. This, however, is not practiced by us;
we place, however, a sign at the end of each line, just as in plain chant, so that the
pitch of the first note of the next system of four lines may be recognized (the custos).
A single rest or notational stem, which has the width of one
space has the durational value of one unit. If the stem is lengthened from one line to the
third one following, or if it covers two spaces, then it occupies two durational units. If
it is even longer and covers all four lines, or the entire width of the stave, then it
occupies the time of three durational units.
It should be noted, that composers of polyphonic music
utilize five lines in their books, although the tenores of descants have only four,
because the tenor is usually taken from plain chant, where it is notated on four lines.
Certain others, for different sections, always use five lines, whether they are following
the method of notating discants or not. This may be seen in simple, double, triple, and
quadruple conductus.
Coussemaker p. 349a34 to p. 350a17
50
In two-voiced, and in the majority of three-voiced
organal compositions, only four lines are used for the tenor, unless the person ruling the
lines has made an error. The upper voices, however, always have five lines. This has been
stated so that if a line is drawn across the entire width of all the spaces, this stem is
considered to have ended the clausula or period.
It should be noted that whenever the brevis is
split into smaller durational values, that this is shown by a line which has the length of
half a space, or by one which does not have the length of an entire space, which if
realized would indicate a rest of one durational unit. Such a stem usually indicates the
equivalence of the third part of a brevis. It is better, however, to draw it even
smaller than necessary.
An example of the semibrevis rest can be shown to
those who know how to reduce modes or change one mode to another, as for example to those
who can derive the second mode from the fifth. They reduce the upper-parts or part
according to the manner of the second mode. This was done by certain Parisians; this is
still done in the case of the Gallican hoquetus In seculum, which was written by
a certain Spaniard. The rests which are found here are called half rests1.
There is also another kind of rest, which looks pike a rest
but really is none, and is called a breath mark. It does not occupy any durational units
in itself, but takes its time values from the sound which immediately precedes it. Thus,
it is quite often found in manuscripts for practical performance, that a stem may indicate
a breath mark or a rest. Such a stem is to be found in the great three-voiced composition Posui
adiutorium in the first clausula or first section, as well as in many other
places. This stem must be drawn as if it were the smallest possible kind of rest and
written obliquely to the previous note in the upper-part, because there is a different
kind of stem which is used in such books in the lower-part. Sometimes these stems are
larger, sometimes smaller, but they never designate any precise time. They are used,
however, to divide syllables, whereby those notes which belong to one syllable are found
on one side, and those which belong to the other on the other side. The same thing is done
when the same word or words are involved, if it is necessary to join them when singing.
You must commit to memory exactly all of these finesses together with those involving many
other kinds of double rests, as will be shown below.
There are others who, when they notate music, use letters in
place of notes, as for example: f f f a c c d c a c c c c e d c c, is found in older books
as the melody of Viderunt omnes (M 1). Contemporary writers do not use letters,
except for the ones at the beginning of the systemata (clefs). Instead, they use round and
square shapes either with or without a stem, and they have cause to write down many such
notes which rise or fall through an octave, fifth, or fourth. They have rules for these
things similar to those inherent in the eight ecclesiastical modes or tones. There is a
different reasoning behind these rules, and they are arranged in a fashion similar to that
of the afore-mentioned (ecclesiastical) modes, although there are other rules.
Coussemaker p. 350a18 to p. 350b35
1) Confer the transcriptions of Nos. 2 and 3 in
Y. Rokseth, loco citato.
51
A double rest is found wherever the single brevis or
longa is doubled or tripled. The first ordo gives an example of all that
will be said subsequently. You should know that ordines of rests can be added
together just like the ordines listed above, etc. There is scarcely any
difference between these different kinds of ordines, as will be shown below.
As far as the above-mentioned double rest is concerned, we
do not mean that the brevis or longa is to be doubled, but rather that
the successive rests are to be understood according to the ordo of the prevailing
mode, or conceived of according to the sequence of note-values. It should even be noted
that in the case of double rests, certain people measure the distance or the amount of
unwritten surface between the two stems. Thus, two stems constitute the equivalence of
three durational units, and three stems represent the equivalence of five durational
units, according to the arrangement of longæ and breves in any
particular mode, as shown in the first ordo of the first mode, etc. In such
cases, however, the stems are all equal in length, and if in the first mode, the music has
a longa, brevis, longa, the rest will be a brevis, longa, brevis. Thus,
the stems will all indicate brevis rests, but the space in between them will
indicate the longa. If you indicate a rest of longa, brevis, longa with
three stems, all of these stems will be longæ, whereas the spaces in between
them will be breves. The ordines of the second mode can be understood in
a similar manner with two or three rests, etc.
If, however, one has a brevis, longa, brevis in the
second mode, then the double rest will have the durational value of a longa, brevis,
longa. In this case, the stems will be formed as longæ, and the spaces
between the three rests will be short, etc. The following rule covers perfect rests: If
the same mode is found both before and after the rest, the rest will be perfect. In this
fashion, you will be able to measure the distances between the rests. Such a procedure is
universally followed in the first, second, and fifth modes; in the case of the second
mode, however, this is utilized only if there is a perfect mode both before and after the
rests, etc.
Again, we can talk about a longa and a brevis followed
by a triple rest, or two equal (longa) rests, which, however, are not used,
because a mode is employed after them which is different from that before. The rests are
drawn as longa, brevis, and longa stems. Then, there will be notes for
the brevis and longa, followed by three stems for the brevis longa
and brevis rests, which are in just the opposite sequence to that which was used
before.
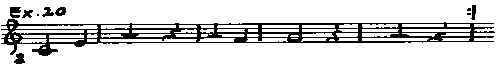
Coussemaker p. 350b36 to p. 351a36
52
The whole succession will be reversed if you are
considering the second mode, substituting the sequence brevis longa (in place of longa
brevis) in the discussion of the notation above.
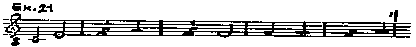
In a similar manner, we may derive the appropriate
sequences for the third and fourth perfect and imperfect modes, as well as for the fifth
and sixth modes, as shown and fashioned above.
Chapter Four
Concerning Harmonic Consonances
In plain chant, thirteen proportions are used. The first
of these proportions is called an unison. The twelve following are named: major second,
minor second, major third, minor third, augmented fourth which is not used very much, the
perfect fourth, the perfect fifth, the major sixth, the minor sixth, the major seventh and
the octave. There are proportions also which are combined with the octave, such as the
major second with octave, the minor second with octave, etc., until one reaches the double
octave; beyond these, is the major second with a fifteenth, the minor second with a
fifteenth etc. up to the perfect fifth and fifteenth; and there are even more notes than
these, such as those used on the organ, where the notes will extend to the triple octave.
Formerly, other writers named these proportions in such a
manner that one proportion was added to another (id est, by multiplication), as
is found in a certain musical rule. They struck out four of these, however, and they said
about these: There are thrice three kinds of proportions which every song contains,
namely: unison, minor second, major second, minor third, major third, perfect fourth,
perfect fifth, major sixth, octave; the augmented fourth, the minor sixth, and the minor
and major sevenths are not used, as shall be exemplified in notation. Thus, there are four
proportions which are not used, etc.
Descriptions and definitions of these proportions can be
understood by the use of the fractional representation of proportionate numbers. Unity is
the distinguishing factor of all things, according to Iordanus the younger. Number is the
total collection of unities. Some numbers are even, others odd. Some numbers are
absolutes, others are relative. Some numbers are perfect, others diminished and still
others excessive. All relative numbers may be arranged according to three different
proportions, others in fewer ways. There are three kinds of proportions. The first kind,
which is called the science of
Coussemaker p. 351a37 to p. 352a12
53
measurement, has the (arithmetic) series: one, two, three, four, five, six, seven,
eight, nine etc. The differences between each of the terms of this series is the same, as
shown fully in the books of the science of mathematics by Boëtius: In dandis
accipiendisque, etc. The second kind involves geometric proportions, such as the
series: two, four, eight, sixteen, thirty two etc., where there are unequal differences
between the terms of the series. This is shown fully in Euclid's geometry; the beginning
of this work is most trying, but the main part isn't. There is another proportion, which
is called the harmonic proportion, and this is partly the same as the arithmetic mean, and
partly the same as the geometric, as shown fully in Boëtius's: Omni quidem perceptio.
The relative proportions may be considered in another
way. Some of them are equal, such as one to one, two to two, three to three, and these are
called equalities by musical theorists, and are named unisons, whether this be heard in
string music, organ pipes or cymbals. The other kind of proportion involves unequal
relationships. This inequality is expressed by five different kinds of inequality which
are called: l. multiplex, 2. superparticularis, 3. superpartiens,
4. multiplex superparticularis and 5. multiplex superpartiens.
We are dealing with the multiplex variety when
a larger number contains an exact multiple of a smaller number; to designate this species,
we use terms such as: double, triple, quadruple etc. Double is realized when the larger
number contains two of the smaller; triple, when it contains three; quadruple, when it
contains four, etc. Double corresponds therefore to the relationship two to one,or four to
two. This is identical to the octave. Two doubles, that is quadruple, constitute the
double octave. In a similar fashion, we can derive the triple octave as used in pipe
organs.
We are dealing with the superparticularis variety
when the larger number contains both the entire smaller number and a mathematical part of
it, etc. The various terms for these are sesquialtera (3/2),
sesquitertia (4/3), sesquiquarta (5/4),
etc. also sesquioctava (9/8). Sesquialtera is
realized when the larger number contains the smaller and half again, and this is called sesquialtera
or emiolius. Sesquitertia is realized when the larger number
contains the smaller and an additional third, and is called epitritus; sesquiquarta
contains the entire smaller number plus a fourth; sesquioctava the entire smaller
number plus an eighth and is called epogdous. Accordingly, the sesquialtera
proportion corresponds to the perfect fifth, and its inversion (id est, 2/3) produces the perfect fourth. Sesquioctava (id est, the
whole tone) is the constitutive element for all of those proportions mentioned before, and
for others, like the smaller and larger half tones, if it is possible to use them. The
octave consists of a fifth and a fourth, in the proportion of 4 : 3 : 2;
the four to two represents the double proportion. Thus, the fifth is 3 : 2
or the sesquialtera proportion, and the fourth is sesquitertia or 4 : 3. Consequently, the octave consists of a fifth and a fourth. All
other musical or harmonic consonances are basically derived from these three consonances.
Coussemaker p. 352a13 to p. 352b28
54
According to others, the fourth is the first of the
consonances. Thus, we find in ecclesiastical (id est, non-musical) writings, that
the fourth is the first consonance, the fifth the second, and the octave the third. This
is one manner of handling the situation, if you evaluate them according to the increasing
size of intervals. Thus, the fourth would be the first symphony (= consonance), the fifth
the second, and the octave the third. If, however, you consider proportions of smaller
number (simpler relationships, to determine the succession of consonances), then the
octave is the greatest of the melodies (= consonances) and the mother of all consonances,
after the basic interval, the unison, since all inequality originates in equality. The
proportion of the octave may, of course, be reduced to that of the unison, as will be
shown below fully. The fifth is the second consonance, and is the next melody (=
consonance) after the octave; the fourth is then the third one, etc. The difference, which
is also called the interval, between the octave and the fifth is the fourth. The
difference or interval between the fifth and the fourth is the major second; consequently,
a major second and a perfect fourth comprise a fifth.
We are dealing with the superpartiens variety when the
larger number contains the smaller number and several parts of it. The various kinds of
these include superbipartiens, supertripartiens, superquadripartiens etc. Superbipartiens
is realized when the larger number contains the smaller number and two parts of it; supertripartiens,
the smaller number and three parts; superquadripartiens the smaller number and
four parts etc., in different manners.
The multiplex superparticularis variety contains
multiples plus one part. The various kinds of these include double sesquialtera, double
sesquitertia etc. Another kind includes triple sesquialtera, triple sesquitertia
etc. In this manner, you can combine all kinds of multiples with all other kinds of superparticulares,
as may be necessary.
The multiplex superpartiens contains all multiples
and several parts. The various kinds of these include: double superbipartiens,
double supertripartiens etc. Another kind includes triple superbipartiens, triple
supertripartiens etc. You can combine just as many multiples with all kinds of superpartientes,
as shown above in the discussion of multiple superparticulares.
The difference or the interval between a major second
and a perfect fourth or their inversion, is the minor third, which is the superquinque
partiens of twenty seven, or 32 : 27. Consequently, the
difference between the minor third and the perfect fourth is the major second, because the
perfect fourth is composed of these two intervals. The difference between the major second
and the minor third is the smaller minor second, which is the supertredecempartiens
of two hundred forty three, or 256 : 243. If you add a perfect fifth
(id est, multiply 256 : 243 by 3/2),
you will have a minor sixth (128 : 81). The difference, thus,
between the minor sixth and the perfect fifth is a minor second. The difference between
the minor second and the perfect fourth, or their inversion, is the major third. Thus, the
perfect fourth is composed of the major third and the minor second, or their inversion.
Thus, the perfect fourth is composed of both of them. The difference between a major
second and a major third is a major second; thus, the major third is composed of two major
seconds, which is the superseptemdecempartiens of sixty four, or 81 : 64.
Coussemaker p. 352b29 to p. 353b6
Anon. IV Part 4.
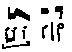 . If five notes are the
equivalence of three, then they would have to be cum opposita proprietate,
whereas four notes would be cum proprietats. In this regard, we again see that
the three-note ligature cum proprietate and cum perfectione is measured longa
brevis, longa according to this theorist.
. If five notes are the
equivalence of three, then they would have to be cum opposita proprietate,
whereas four notes would be cum proprietats. In this regard, we again see that
the three-note ligature cum proprietate and cum perfectione is measured longa
brevis, longa according to this theorist.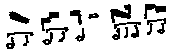 where
the three-note ligature still has the modal significance of an initial longa, whereas the
substitute form has been made mensural (id est, sine proprietate).
where
the three-note ligature still has the modal significance of an initial longa, whereas the
substitute form has been made mensural (id est, sine proprietate).  or
or 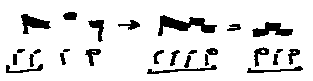 . The following paragraph is repetitious in Coussemaker's text and is
omitted.
. The following paragraph is repetitious in Coussemaker's text and is
omitted.