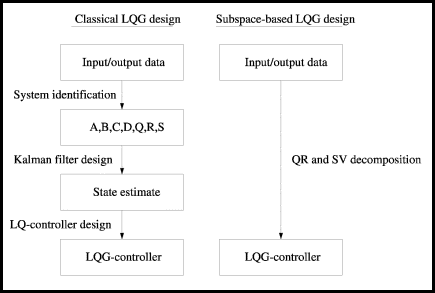
Comparison between the classical and the subspace-based LQG-design method.
Bart De Moor, Wouter Favoreel
The problem of designing a model-based controller for a system often consists of the following three different steps: system identification, observer design, state feedback design. Although strongly related, in the literature these steps are hardly ever considered as one integrated problem. Most authors restrict themselves to the study of one of the three topics.
The aim of this research is to make the link between the by now well-known subspace system identification techniques and linear optimal/predictive control methods. The method we propose is based on subspace identification techniques. Starting from an unknown system, it provides the user with a finite horizon LQG-controller, directly from a set of measurements of the inputs and the outputs of the system. The system identification step, the Kalman filter step and the LQ controller design are inherent to the way of solving the problem and are replaced by elementary operations of linear algebra such as QR and SV decompositions.

Comparison
between the classical and the subspace-based LQG-design method.