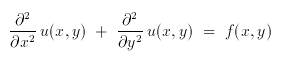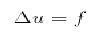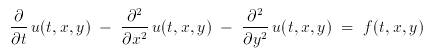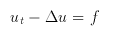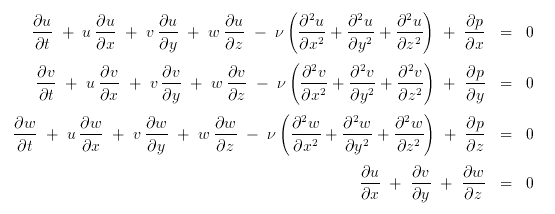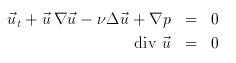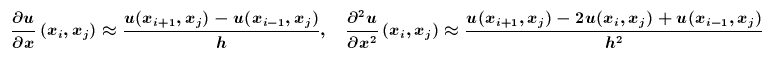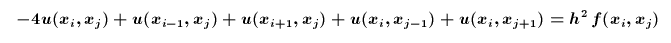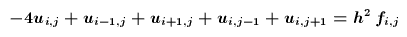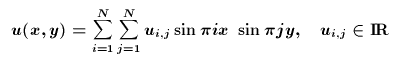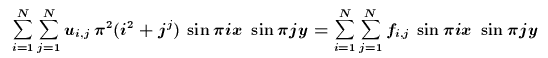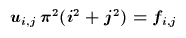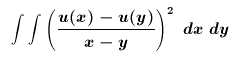Ein Einstieg in das Gebiet meiner Dissertation (für Laien)
Meine Dissertation fällt in das Gebiet Numerik partieller Differentialgleichungen.
Das praktische Problem, zu dessen Lösung diese Dissertation beitragen soll, ist die Simulation von Strömungen (Flüssigkeiten oder auch Gas/Luft) in einem Kanal, und zwar die Umströmung von gewissen Hindernissen, die sich im Kanal befinden. Da wir uns hauptsächlich für mathematische Grundlagenforschung interessieren, simulieren wir einfach die Umströmung eines zylinderförmigen Hindernisses. Die tatsächlichen 'real world'-Probleme, auf die man es abgesehen hat, sind eher die Umströmung von Autos, Schiffen, Flugzeugen. Auf diese Lässt sich unser Verfahren natürlich ebenfalls anwenden.
Was ist Numerik?
Die Numerik ist der Teil der Mathematik, der für Probleme, für die man keine exakte Lösung angeben kann, mit Hilfe des Computers Näherungslösungen sucht. Es werden Verfahren entwickelt, mit denen man, wenn man nur genügend Rechenzeit investiert, beliebig genaue Näherungslösungen angeben kann. Besonders beliebt sind sog. iterative Verfahren: Ausgehend von einer beliebigen Näherungslösung wendet man eine bestimmte Rechenvorschrift an, und bekommt so eine bessere Näherungslösung. Auf diese wiederum wendet man wieder die gleiche Rechenvorschrift an, und bekommt so eine noch genauere Näherungslösung. Und so weiter. Ein sehr bekanntes, 'klassisches' iteratives Verfahren ist z.B. das Newton-Verfahren zum Aufspüren von Nullstellen von Funktionen. Im wesentlichen hat sich die Numerik erst in der 2. Hälfte des 20. Jahrhunderts entwickelt, denn die meisten Verfahren der Numerik sind erst interessant geworden, seit es Computer gibt. Auch das CGBI-Verfahren, das das Hauptthema meiner Dissertation ist, ist so ein iteratives Verfahren, das allerdings dazu dient, eine partielle Differentialgleichung zu lösen, und zwar so, daß die Arbeit auf mehrere Computer/Prozessoren verteilt werden kann.
Was ist eine partielle Differentialgleichung?
Am besten lässt sich das an Hand eines Beispiels verdeutlichen:
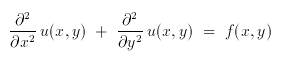
Dies ist die sog. Poisson-Gleichung. Gegeben ist die Funktion f(x,y), und gesucht ist eine Funktion u(x,y), die die obige Gleichung erfüllt. Das d^2u/dx^2 steht dabei für die zweite Ableitung der Funktion u nach x.
In Kurzschreibweise sieht die Poisson-Gleichung so aus:
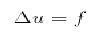
Dabei ist das Dreieck der sogenannte Laplace-Operator.
Allgemein ist eine partielle Differentialgleichung eine Gleichung, die einen Zusammenhang zwischen den partiellen Ableitungen einer Funktion, die gesucht wird, herstellt.
Partielle Differentialgleichungen hat man nicht erfunden, um den Spieltrieb der Mathematiker zu befriedigen; nein, sie kommen bei Naturvorgängen häufig vor. Z.B. bei der Bestimmung von Minimalflächen (das Dach des Münchner Olympiastadions, Seifenblasen), bei der Beschreibung von Wärmeleitungsvorgängen in Körpern und Gasen, bei der Wettervorhersage, der Klimavorhersage, bei Strömungsprozessen, bei Verformungen fester/elastischer Körper wie Autoreifen oder Autos, die gegen Bäume fahren. Wer sich für mathematischen Formalismus nicht interessiert, der überspringe den Rest dieses Abschnitts.
Ein weiteres Beispiel für eine partielle Differentialgleichung:
Die berümte Wärmeleitungsgleichung lautet
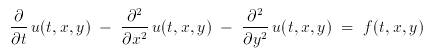
kurz
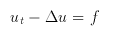
wobei t die Zeit ist.
Meine Dissertation beschäftigt sich mit der partiellen Differentialgleichung, die Strömungsprozesse beschreibt: Die Navier-Stokes-Gleichung. Sie sieht leider etwas komplizierter aus:
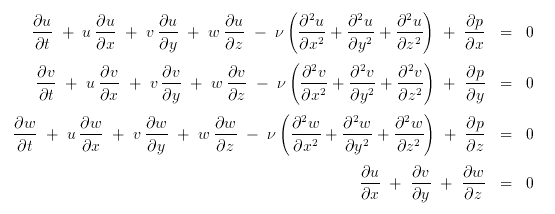
Zum Glück gibt es die mathematische Kurzschreibweise:
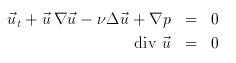
Dabei sind u, v, w die drei Komponenten der Geschwindigkeit an einem Ort (x,y,z) zur Zeit t, und p ist der Druck dort. Das auf der Spitze stehende Dreieck bezeichnet den Gradienten, was soviel wie eine Verallgemeinerung der ersten Ableitung ist: grad u = (du/dx,du/dy,du/dz); grad u ist valso eine vektorwertige Funktion.
Ein wesentlicher Aspekt, worin sich die Navier-Stokes-Gleichung von den vorhergehenden Gleichungen unterscheidet, ist, dass sie nichtlinear ist. Das heißt, dass in den Gleichungen unbekannte Funktionen miteinander multipliziert werden. Dies macht theoretische Untersuchungen sehr viel schwerer. Zum Beispiel wurde erst in den 50er Jahren bewiesen, dass diese Gleichung überhaupt eine Lösung hat! Und viele wichtige Eigenschaften sind heute noch unbekannt, obwohl sich weltweit einige Tausend Mathematiker mit dieser Gleichung beschäftigen dürften! Mit Hilfe eines Verfahrens aus den 60er Jahren (Druck-Korrektur-Verfahren) ist es möglich, jeden Navier-Stokes-Zeitschritt in drei einfachere Probleme zu zerlegen. Eines dieser drei Probleme ist die Poisson-Gleichung, daher wird dieser Gleichung in meiner Dissertation besonders viel Aufmerksamkeit gewidmet.
Was sind Randbedingungen? Am liebsten beschäftigt sich der Mathematiker mit Problemen, die eine Lösung haben. Noch lieber sind ihm Probleme, die genau eine Lösung haben. Nehmen wir das Beispiel von oben, die Poisson-Gleichung (siehe oben), und zwar für den besonders einfachen Fall f(x,y)=0. Man sieht leicht, dass es ziemlich viele Lösungen gibt: Alle Funktionen u der Art u(x,y)=a+bx+cy, oder auch u(x,y)=exp(cx)sin(cx). Wir brauchen also noch eine weitere Bedingung, um eine sinnvolle Fragestellung zu bekommen. Zum Beispiel könnte man fordern, dass an allen Punkten (x,y), die auf dem Rand eines Gebietes Omega liegen, u(x,y)=1 gelten soll. Schon hat die Poisson-Gleichung nur noch eine einzige Lösung, nämlich u(x,y)=1 auf ganz Omega. Probleme, die keine Lösung oder aber mehrere Lösungen haben, nennt der Mathematiker schlecht gestellt (auf englisch noch drastischer 'ill posed'). Er will damit zum Ausdruck bringen: "Nicht ich bin Schuld, dass da nichts 'rauskommt, sondern das Problem an sich!"
Die Notwendigkeit von Randbedingungen lässt sich auch anschaulich klarmachen:
Das Verhalten einer Seifenblase ('Minimalfläche'), die sich in einem verbogenen, in sich geschlossenen Draht befindet (gegen die ggf. gepustet wird; die rechte Seite f in der Poisson-Gleichung gibt dann die Kraftdichte, mit der gepustet wird, an), wird durch eine partielle Differentialgleichung beschrieben. Die Form des Drahtes (des Randes der Seifenblase) wird durch Randbedingungen beschrieben. Bei Strömungsvorgängen in einem Kanal benötigt man Randbedingungen, die angeben, wie viel und in welcher Weise Flüssigkeit in den Kanal hineinströmt. Außerdem noch Anfangsbedingungen, die angeben, welche Strömung im Innern des Kanals zum Zeitpunkt, bei dem die Simulation startet, vorliegt.
Im Fall von Strömungen (allgemein bei zeitabhängigen Problemen) nimmt man den gegebenen Anfangszustand der Strömung im Kanal und berechnet daraus mit einem numerischen Näherungsverfahren den Zustand zu einem neuen Zeitpunkt, z.B. nach 0,05 Sekunden. Dann nimmt man diesen Strömungszustand und berechnet daraus einen neuen Zustand zum Zeitpunkt t=0,010 Sekunden usw. Man macht also einen Zeitschritt nach dem anderen.
Wer Formeln und Gleichungen nicht mag, der überschlage den folgenden Abschnitt.
Zunächst mal ohne Parallelisierung: Wie findet man eine Näherungslösung einer partiellen Differentialgleichung? Dazu sind schon viele Verfahren erfunden worden. Alle laufen darauf hinaus, dass die Differentialgleichung (die an an unendlich vielen Punkten erfüllt werden soll) duch ein Gleichungssystem mit endlich vielen Gleichungen und Unbekannten ersetzt wird. Dies kann dann im Computer gelöst werden. Man nennt diesen Übergang Diskretisierung.
Beschränken wir uns auf das Beispiel der Poisson-Gleichung. Wir wollen 2 verschiedene besonders einfache numerische Verfahren erwähnen:
- Die Finite Differenzen Methode (FDM): Man legt ein Netz von Gitterpunkten mit äquidistantem Abstand in das Rechengebiet. Man approximiert nun z.B.
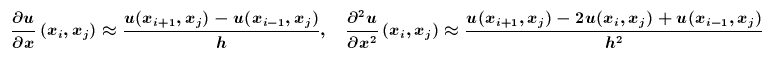
Zumindest die linke der beiden Näherungsformeln sollte einleuchtend sein: Man hat einfach den Differentialquotienten durch einen Differenzenquotienten ersetzt. Die rechte der beiden Formeln bekommt man dann, indem man den Differenzenquotienten von Differenzenquotienten bildet. (Ups, in der linken Formel fehlt im Nenner ein Faktor 2.)
Setzt man dies in die Differentialgleichung ein, so bekommt man ein lineares Gleichungssystem, das so viel Gleichungen und Unbekannte hat, wie man Gitterpunkte gewählt hat. Für die oben beschriebene Poisson-Gleichung bekommt man:
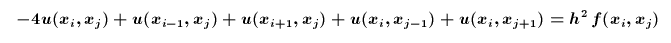
Kurz:
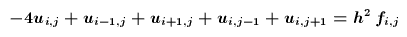
- Spektralmethoden (Fourier-Methoden): Man denkt sich die gesuchte Funktion u(x,y) zerlegt in eine Reihe von Schwingungen oder von anderen 'Basis'-Funktionen, also z.B.
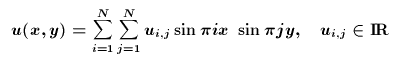
Da man die partiellen Ableitungen dieser Schwingungen sehr schön ausrechnen kann, setzt man diesen Ansatz in die Differentialgleichung ein und bekommt
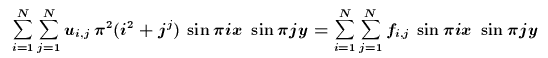
also, per Koeffizientenvergleich,
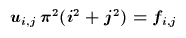
Da man f(x,y) und damit auch die f_i,j kennt, kennt man nun auch die Koeffizienten in der Reihenentwicklung von u(x,y) und damit in gewisser Weise u(x,y) selbst. Es bleibt anzumerken, dass das Spektralverfahren in meiner Dissertation als Basisfunktionen keine Sinus-Schwingungen, sondern gewisse Polynome (Tschebyschev-Polynome) verwendet. Der Grund: Bei Verwendung dieser Polynome braucht man viel weniger Reihenglieder, um eine Funktion gut zu approximieren, als wenn man stattdessen Sinus und Cosinus verwendet.
Wozu Parallelisierung? Um die Strömungsgleichungen zu lösen, sind seit den 60er Jahren schon viele Verfahren entwickelt worden.
Unser CGBI-Verfahren ist ein paralleles Verfahren. Das heißt, dass CGBI ermöglicht, die Berechnung der Strömung auf mehrere Computer oder Prozessoren zu verteilen! Das gesamte Rechengebiet (also der Kanal) wird in soviele Teilgebiete eingeteilt, wie man Computer bzw. Prozessoren zur Verfügung hat. Jeder Computer rechnet dann nur auf seinem Teilgebiet.
Die Parallelisierung dient in erster Linie dazu, die Berechnung schneller zu machen. Gerade die Strömung um kompliziertere Gegenstände (Autos, Flugzeuge) ist dermaßen aufwendig, dass auch heute noch die schnellsten Supercomputer der Welt überfordert sind! Immer mehr Prozessoren sind notwendig, um immer genauere Simulationen zu ermöglichen. Obwohl heutige Rechner viele Milliarden Operationen pro Sekunde ausfüren können, müsste sich ihre Leistungsfähigkeit noch mal um -sagen wir mal- einen Faktor von einer Million steigern, um eine wirklich gute Simulation der Strömung um ein Düsenflugzeug zu ermöglichen. (Ich persönlich würde nicht in ein Flugzeug steigen, dessen Flugeigenschaften nur berechnet wurden, und die nicht auf Experimenten und Erfahrungswerten von Ingenieuren beruhen!)
Ein anderer Grund ist, dass die Parallelisierung ermöglicht, auf verschiedenen Teilen des Gebietes verschiedene mathematische Methoden anzuwenden. So gibt es z.B. Methoden, die ultra-effizient sind, die aber leider nur auf rechteckigen Rechengebieten funktionieren: Die sog. Spektralmethoden (siehe oben). Auf kompliziert geformten Teilen des Rechengebietes kann man Spektralmethoden nicht anwenden. Dort sollte man zu sogenannten Finite-Elemente-Methoden (FEM) greifen. FEM zerlegt ein beliebig vorgegebenes Rechengebiet in viele kleine Dreiecke und kommt so auch mit komplizierten Gebieten klar. Bei FEM nimmt man dann (meist) an, dass die Lösung auf jedem einzelnen dreieckigen Element linear (d.h. eine schiefe Ebene) ist.
Unser CGBI-Parallelisierungsverfahren ermöglicht, das Rechengebiet so aufzuteilen, dass man viele rechteckige Teilgebiete hat, auf denen man das effiziente Spektral-Verfahren benutzen kann, und auf den übrigen Gebieten, die sich um das Hindernis gruppieren, FEM verwenden kann. So kann man die Vorteile beiden Methoden vereinen.
Was ist an der Parallelisierung so schwer? Stellen wir uns das Problem einer Seifenblase in einem geschlossenen Drahtramen vor. Ausserdem wirke auf die Blase eine 'äußere Kraft'; z.B. indem wir leicht dagegen pusten. Wir zerlegen das Gebiet, also die vom Drahtrahmen umschlossene Fläche, in mehrere Teilgebiete, und weisen jedem unserer Prozessoren ein Teilgebiet zu.
Nun haben wir aber oben schon erfahren, dass man zum Lösen einer partiellen Differentialgleichung auf dem Rand Randbedingungen benötigt. Auf dem Rand des Gesamtgebietes haben wir Randbedingungen, nämlich durch die Form des Drahtes vorgegeben. Was ist aber auf den Teilgebieten? Auf deren Rändern, den sog. künstlichen Rändern zwischen den einzelnen Teilgebieten, haben wir keine Randbedingungen zur Verfügung. Wir müssten wissen, wie der Verlauf der Seifenblase auf diesen künstlichen Rändern ist. Wenn wir dies wüssten, könnten wir diese Daten als Randbedingungen benutzten, und jeder der Prozessoren wüsste, was er zu tun hätte.
Sinn und Zweck von CGBI ist es, diese Randbedingungen auf den künstlichen Rändern zwischen den Teilgebieten zu finden!
Wodurch unterscheidet sich CGBI von anderen Parallelisierungsmethoden? In der Tat macht man sich seit den frühen 80er Jahren Gedanken um die Parallelisierung der Lösung von partiellen Differentialgleichungen. Ein wesentlicher Unterschied von CGBI zu den anderen Methoden ist die Art der Randbedingung, die wir auf den künstlichen Rändern suchen. Während die übrigen Methoden Randbedingungen vom sog. Dirichlet'schen Typ (d.h. der Funktionswert auf dem Rand wird vorgegeben) suchen, sucht CGBI nach Randbedingungen vom Neumann'schen Typ (d.h. die Ableitung der Funktion am Rand wird vorgegeben). Ein weiterer wesentlicher Unterschied zu den anderen Methoden wird weiter unten noch genannt: Die Vorkonditionierung.
Wie funktioniert CGBI? Wie findet man nun diese Randbedingungen? CGBI ist eine iteratives Verfahren. Es startet zunächst mal mit willkürlichen Neumannschen Randbedingungen auf den küstlichen Rändern. Die Ergebnisse, die die Prozessoren dann liefern, werden verglichen. Da die Randbedingungen willkürllich waren, ist die Lösung, die die Prozessoren lieferten, natürlich nicht korrekt; sie weist vielmehr Sprünge an den künstlichen Rändern auf! (Man stelle sich eine Seifenblase mit Sprüngen vor!) CGBI analysiert nun diese Sprünge und berechnet daraus neue, bessere Randbedingungen, mit denen dann das Verfahren wiederholt wird. Diese neue Näherungslösung wird dann kleinere Sprünge aufweisen. Und wenn man die Prozedur oft genug wiederholt hat, sind praktisch keine Sprünge mehr vorhanden; die 'wahre' Lösung ist bekannt.
Bei unserem CGBI ist es so, dass sich die Sprünge von Schritt zu Schritt um etwa eine Zehnerpotenz verringern! Nach etwa 8 Schritten schon hat man die Sprünge also um einen Faktor 10^(-8) reduziert! Das ist i.a. genau genug.
Wie schafft es CGBI, dass die Sprünge immer kleiner werden? CGBI stellt einen Zusammenhang her zwischen den gerade verwendeten Neumannschen Randbedingungen und den auftretenden Sprüngen der Näherungslösung. Das Problem wird so formuliert: Suche nach denjenigen Neumannschen Randbedingungen, so dass die Sprünge minimal (nämlich null) werden! CGBI hat also ein sog. Minimierungsproblem zu lösen.
Wie kann man sich so ein Minimierungsproblem anschaulich vorstellen? Stellen wir uns eine Landkarte als Relief vor. Wir stehen irgendwo auf diesem Relief und suchen nun nach dem Minimum, also der tiefsten Stelle. Wie können wir vorgehen? Wir machen einen Schritt in diejenige Richtung, in die es am steilsten bergab geht. Vom neuen Standpunkt aus machen wir wieder einen Schritt in diejenige Richtung, in die es am steilsten bergab geht, usw. (Genau so verhält sich übrigens Wasser, das aus einer Quelle strömt; es fließt in diejenige Richtung, in die es am steilsten bergab geht. Meist erreicht es dadurch irgendwann das Meer, sofern es nicht in einem 'lokalen Minimum' wie dem Kaspischen Meer oder einem Salzsee gefangen wird.) Der Pfeil, der in die Richtung, in der es am steilsten bergauf geht, zeigt, nennt der Mathematiker den Gradienten. Das Negative vom Gradienten ist also der Pfeil, der in die Richtung des steilsten Abstiegs zeigt. Daher nennt man dieses Verfahren das Gradientenverfahren. In den 50er Jahren erfuhr das Gradientenverfahren eine gigantische Verbesserung und wurde so zur Methode der konjugierten Gradienten, conjugate gradient method, kurz: CG-Verfahren. CGBI benutzt, um sein Minimierungsproblem zu lösen, das CG-Verfahren. Dies erklärt schon man die erste Hälfte der Abkürzung CGBI. Das 'BI' in CGBI steht für boundary iteration. Das soll andeuten, dass unsere Iteration auf den Rändern zwischen den Subgebieten stattfindet (dort werden ja abwechselnd die Sprünge und die Randbedingungen errechnet).
Wie ist das mit der Effizienz?
Was iterative Verfahren angeht, so möchte man natürlich nach möglichst wenigen Iterationsschritten möglichst nahe bei der gesuchten Lösung sein. Damit steht und fällt ein Verfahren. Wir sind der Meinung, dass CGBI ein besonders effizientes Verfahren ist. Wie oben schon gesagt, erreichen wir eine Verkleinerung des Fehlers um einen Faktor 10 pro Iterationsschritt, was wirklich nicht schlecht ist (manche klassische Iterationsverfahren erreichen eine Fehlerreduktion von 1 Prozent oder 0,1 Prozent pro Iterationsschritt, d.h. man muss hunderte von Iterationsschritten machen, um eine Zehnerpotenz an Genauigkeit zu gewinnen). Wie schafft CGBI es, so schnell zu konvergieren?
Jedem Minimierungsproblem kann man eine gewisse Matrix zuordnen. Die Geschwindigkeit eines Iterationsverfahrens hängt von dieser Matrix; genauer gesagt vom Verhältnis des größten zum kleinsten Eigenwert dieser Matrix ab. (Eine Zahl c heißt Eigenwert einer Matrix A, wenn es einen Vektor x von 0 verschieden gibt, so daß Ax=cx gilt.) Leider ist dieses Verhältnis bei praktisch auftretenden Minimierungsproblemen immer ziemlich groß und die CG-Konvergenz daher ziemlich langsam. Um ein CG-Verfahren (wie CGBI) zu 'beschleunigen' setzt man die sog. Vorkonditionierung ('Preconditioning') ein: Man ersetzt das Minimierungsproblem bzw. seine Matrix durch ein äquivalentes Minimierungsproblem und seine Matrix, so dass diese neue Matrix ein viel günstigeres Verhältnis von größtem zu kleinstem Eigenwert hat. Das gesamte dritte Kapitel meiner Dissertation widmet sich dem Thema, wie man effiziente Vorkonditionierer (Preconditioner) konstruieren kann. Die Art (und, wie wir meinen, die Effizienz) unserer Vorkonditionierer ist ein weiterer Unterschied zu anderen Parallelisierungsverfahren.
Was lässt sich über die Konstruktion unserer Vorkonditionierer noch sagen? Die Erklärung, wie diese Vorkonditionierer konstruiert werden, würde viel zu sehr in die Tiefe führen. Ich möchte nur auf eine der dabei verwendeten mathematischen Methoden hinweisen: Die Verwendung gebrochener Ableitungsordnungen.
Zunächst mal zur Frage, was man in der Numerik überhaupt unter Differenzierbarkeit (d.h. Ableitbarkeit) versteht. In der Schule lernt man, wann eine Funktion differenzierbar ist: Wenn der Grenzwert des Differenzenquotienten existiert. Diese Art der Definition von Differenzierbarkeit nennt man in der Mathematik 'starke Differenzierbarkeit'. Es hat sich im Laufe des 20. Jahrhunderts herausgestellt, dass man mit diesem Begriff nicht auskommt: Viele Differentialgleichungen, die Naturvorgänge beschreiben, verwenden erste und zweite Ableitungen, obwohl die in der Natur vorliegenden 'Lösungen' dieser Probleme Ecken und Knicke haben, also gar nicht 'stark' differenzierbar sind!
Der Ausweg war, einen 'schwachen' Differenzierbarkeitsbegriff, den Begriff der 'schwachen Ableitung' einzuführen: Wenn eine beliebige Funktion sich in einem gewissen Sinne durch stark differenzierbare Funktionen approximieren lässt, und wenn die zugehörige Folge der starken Ableitungen ebenfalls konvergiert, dann nennt man den Grenzwert dieser Folge von starken Ableitungen die schwache Ableitung der gegebenen Funktion. Funktionen mit 'Knicken' werden nun auch erfasst; sie sind 'schwach differenzierbar'. Die Einführung dieses Begriffs hatte enorme Auswirkungen; Differentialgleichungen, für die man vorher keine 'klassischen' Lösungen finden konnte, haben nun Lösungen (sog. schwache Lösungen), und es haben sich ganz neue Gebiete der Mathematik entwickeln können.
Wem das noch nicht abgedreht genug ist, dem möchte ich noch den Begriff der gebrochenen Ableitungsordnung nahebringen: Allgemein bekannt sind Ableitungen der 1., 2., 3. Ordnung. Nun kann man als Mathematiker sich dranmachen, auch Ableitungen der 1/2. Ordnung, allgemein der s-ten Ordnung, mit s aus der Menge der reellen Zahlen (auch negative!) zu definieren! All die Funktionen, deren Ableitung einer festen Ordnung existieren, bilden zusammen einen Funktionenraum, genauer gesagt einen Hilbert-Raum. Die Funktionen, die 1/2 mal differenzierbar sind, bilden den H^(1/2), der in meiner Dissertation so oft vorkommt. Lustigerweise hat die Arbeit mit solchen Ableitungsordnungen sehr viel mit Integralen zu tun. Z.B. kann man den Raum H^(1/2) charakterisieren als Menge aller Funktionen u(x), für die das Doppel-Integral
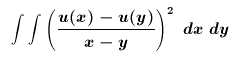
existiert.
Ohne die Theorie der gebrochenen Ableitungsordnungen, die ja zunächst vielleicht ziemlich theoretisch erscheint, hätte ich meine Vorkonditionierer nicht entwickeln können, und unser Parallelisierungsverfahren müsste 100 statt 8 Iterationsschritte machen!
Was ich bisher geschildert habe, ist nur ein kleiner Einstieg in das Thema. Nichts, was nicht schon vor meiner Dissertation bekannt gewesen wäre.
Doch wenn man in die eigentlichen Fragestellungen meiner Dissertation einsteigen will, kommt man um den mathematischen Formalismus nicht mehr herum. Wer sich dafür interessiert, der solle Mathematik studieren! Noch eine Anmerkung zur Numerik: Man hat hier vielleicht den Eindruck gewonnen, in der Numerik wird alles, was man nicht lösen kann, einfach irgendwie angenähert, d.h. es wird sich bei der Numerik um eine Ansammlung von ziemlich diffusen Ideen handeln. Nichts wäre falscher!! All die Näherungen werden genau untersucht, d.h. man untersucht, wie groß die gemachten Abweichungen sind und wovon sie abhängen, und wie man mit weniger Rechenaufwand zu besseren Näherungen kommt. Alles wird streng bewiesen! Die mathematische Exaktheit und auch die mathematische Abstraktion in diesem Gebiet der Mathematik steht der in anderen Gebieten der Mathematik um nichts nach. Ein Unterschied der Numerik zur zur 'reinen Mathematik' ist, dass man am Ende bunte Bilder bekommt, die dann auch noch einen Bezug zur 'realen Welt' haben (siehe am Ende meiner Dissertation).
zurück