|
Konzeptdesign für die räumliche hybride Analyse
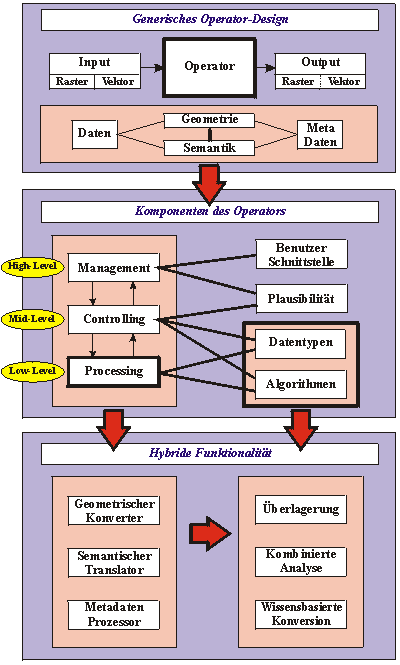
| Die räumliche hybride Analyse verarbeitet Geodaten in Raster- und Vektorrepräsentation gemeinsam, ohne dabei eine Konversion zwischen den Datenstrukturen durchzuführen. Dabei werden geometrische wie semantische Informationen aus beiden Repräsentationen zueinander in Beziehung gesetzt, um dabei neue geometrische und semantische Information zu erzeugen. Diese Informationsgewinnung erfolgt durch eine hybride geometrische und semantische Interaktion. |
Dieser Ansatz ist eine funktionale Erweiterung der räumlichen Analyse auf struktureller und algorithmischer Ebene. Er setzt voraus, daß die zu verarbeitenden Geodaten bereits semantisch modelliert sind. Der Kern dabei ist die Verarbeitung von Geodaten in Vektor- und Raster-repräsentation ohne Datenkonversion, um dabei einer Konversion entstehenden geometrischen wie semantischen Informations- und Genauigkeitsverluste möglichst zu vermeiden.
Der hybride Ansatz für die räumliche Analyse unterscheidet sich von der Funktionalität in der Datenerfassung denn letztere versucht, aus uninterpretierten und/oder ungeordneten Strukturen und Informationen eine semantische Ordnung herzustellen. In beiden Fällen jedoch können dieselben geometrischen Prinzipien Geltung haben.
Eine hybride Analyse verlangt (wie generell bei der gemeinsamen Verarbeitung von Geo-daten), daß die zu verarbeitenden Daten sowohl physisch wie mathematisch denselben Raum-bezug besitzen, damit eine räumliche geometrische Überlagerung stattfindet. Dieses Kriterium impliziert die Forderung z.B. nach einer identischen Funktionalität für die Georeferen-zierung von Raster- und Vektordaten. Siehe [Voser 1998a]. Der gemeinsamer Raumbezug ist hergestellt durch:
denselben geographischen Raum
dasselbe Koordinatenreferenzsystem.
Von Bedeutung wird zudem das hybride metrische Konzept, welches an die kombinierte Verarbeitung angepaßt werden muß. Auf der einen Seite bedeutet dies unterschiedliche Definitionen der Abstandsfunktion im stetigen Vektorraum und im diskreten Rasterraum (Kapitel 5.2), welche im speziellen die funktionale Implementierung und deren Algo-rithmik beeinflussen. Auf der anderen Seite sind es weitere metrische Kenngrößen, welche mitunter von der zugrundeliegenden Metrik abhängen. Schlüsselbegriffe dabei sind:
Unschärfe als empirische Unbestimmbarkeit
Auflösung basierend auf dem deterministischen Abstandsfunktional der Metrik
Genauigkeit als stochastisches Wahrscheinlichkeitsmaß.
Weitere Begriffe im Kontext metrischer Kenngrößen sind:
Maßstab
Unsicherheit.
Die metrischen Kenngrößen sind voneinander abhängig wie das Huhn vom Ei und vice versa. Sie haben sowohl Gültigkeit für die Objekte, deren Modellierung und Erfassung, Strukturierung sowie für die Prozesse und Operationen, welche angewandt werden. Ein Problemfeld im Kontext der metrischen Kenngrößen und der Strukturierung von Geodaten liegt darin, daß der Anwender den Vektordaten durch deren geometrische Vielfalt eine höhere Genauigkeit impliziert gegenüber der der Rasterdaten.
5 Die geometrische Interaktion
- 5.1 Hybride Strukturen
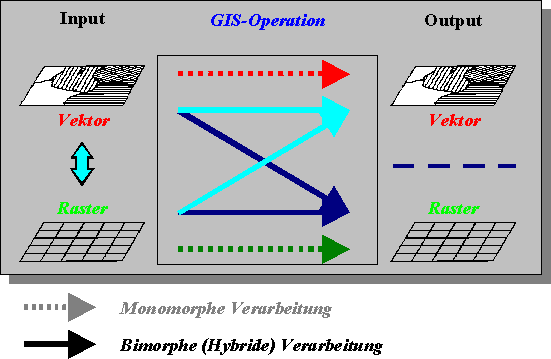
Die Geometrie und deren unterschiedliche Strukturierung bildet die Ursache und trägt den Kern der hybriden Analyse. Der Vektorraum kann als stetiger Raum betrachtet werden (bis auf die Ein-schränkungen der digitalen Repräsentation), während der Rasterraum diskret ist. Im Vektor-raum können freie Geometrien vorliegen, während Raster auf festen Strukturen aufbaut. Der Vektorraum setzt dabei auf der 0-dimensionale Primitive (Punkt) auf, verwendet Linien als 1-dimensionale Primitiven und Flächen als 2-dimensionale Primitiven. Linien und Flächen besitzen neben der Position noch Form, Orientierungs- und Größenparameter. Der Rasterraum setzt auf der festen Struktur der regelmäßigen Anordnung der Informationsträger auf. Diese sind punkt- oder flächenhaft. Neben der Position des Ursprungs der Rasterzellen oder -punkten sind deren Orientierung und die Rasterweite (Auflösung) metrikbildend.
Die geometrische Interaktion umfaßt minimal die geometrische Überlagerung inklusive Suche und Verschneidung von Raster und Vektorprimitiven. Das entscheidendste Kriterium der hybriden Interaktion ist deren Verwandtschaft im Sinne der Art der Überlagerung und interagierenden Selektion. Dies steht in Abhängigkeit mit den metrischen Eigenschaften wie z.B. Längen und Flächen sowie die Vielzahl möglicher Berührungseigenschaften.
- 5.2 Metriken im hybriden Raum
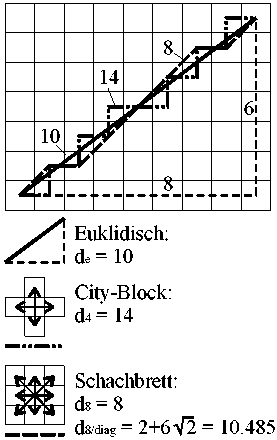
Die Metrik raumbezogener Daten wird den Koordinaten und deren zugrundeliegendem Koor-di-natenreferenzsystem zugewiesen. Bei der Betrachtung des hybriden Raumes in der Ebene treten verschiedene Definitionen der Metrik im Vektor- wie im Rasterraum auf, welche das Abstandsmaß unterschiedlich festlegen. Die wichtigsten davon sind:
Euklidische Metrik 
City-Block Metrik (4er-Umgebung)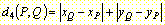 
Schachbrett-Metrik (8er-Umgebung)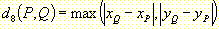 
Die unterschiedlichen Metriken liefern unterschiedliche Maßinformationen, z.B. jene der Länge. Das in Abb. 4 dargestellte Beispiel zeigt die Abweichungen der City-Block und der Schachbrett-Metrik von der Euklidischen Distanz. Bei der Schachbrett-Metrik ist ein weiteres Maß dargestellt, welches die Diagonalen mit
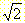berücksichtigt.Die unterschiedlichen Metriken beeinflussen die Algorithmen essentiell, denn sie sind strukturbedingt. Es müssen in Zukunft Methoden entwickelt werden, welche den Brücken-schlag zwischen diesen Metriken herstellen.
- 5.3 Aspekte der geometrischen
Interaktion
Die hybride geometrische Interaktion beinhaltet die Kernproblematik für die hybride Analyse. Die unterschiedlichen geometrischen Charakteristiken fordern im Raster- und im Vektorraum unterschiedliche Algorithmen für dieselben funktionalen Modelle räumlicher Analyse, stützen sich dabei auf unterschiedliche metrische Konzepte. Diese müssen jedoch auf das zugrundeliegende Koordinatenreferenzsystem angepaßt werden.
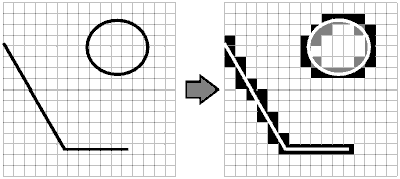
Im Zentrum der hybriden geometrischen Inter-aktion stehen die hybride Suche, die hybride Überlagerung, die hybride Verschneidung. Die Identifikation interagierender geometrischer Primitiven ist der erste Schritt. Die unterschiedlichen Möglichkeiten der Selektion, z.B. nach der Art der Über-lagerung, beeinflussen die metrische Eigen-schaften wie die z.B. den Flächeninhalt. An solcher Stelle kommen Konzepte der Sub-pixelklassifikation zum Tragen (z.B. [Tomlin 1990], um damit genauere hybride Nachbar-schaftsklassifikationen durchführen zu können, welche sich z.B. in der metrischen Genauigkeit widerspiegeln. In Abb. 5 ist das Prinzip der hybriden Überlagerung, z.B. mit unterschiedlicher Pixelklassifikation einer flächenhaften Überlagerung, dargestellt.
6 Semantische Interaktion
- 6.1 Die Ebenen der Semantischen
Interaktion
Die semantische Interaktion setzt die (geo-)metrische Interaktion voraus. Sie gliedert sich in eine strukturell-geometrische, eine logische sowie eine thematische Komponente.
Die strukturell-geometrische Komponente der semantischen Interaktion steht über der me-trischen Ebene der räumlichen Überlagerung, Verschneidung und Suche infolge der Berück-sichtigung der strukturellen Komponente, bestehend aus den geometrischen Primitiven wie auch der auf der Objekt- und Phänomenbildung und Modellierung. Ein Problemfeld in diesem Kontext betrifft die Grenze des Übergangs von einer Linie zur Fläche oder umgekehrt, welche stark mit der Unschärfe, der Genauigkeit, der Auflösung und dem Maßstab sowie dem Gene-ralisierungsgrad korrelieren. Diese Ebene der Interaktion ist noch direkt von der Kernproble-matik der Hybridität betroffen und berührt die Algorithmik der Prozessierungs- und Controlling-Ebene eines Operators.
Die logische Komponente der semantischen Interaktion beinhaltet die logische Objekt- und Phänomenbildung und deren Wechselwirkung. Dazu gehört die Modellierung in hierarchischen, netzwerkartigen oder Ebenen-Modellen. Diese Ebene der semantischen Interaktion betrifft in erster Linie die Controlling-Ebene eines Operators.
Die thematische Komponente der semantischen Interaktion betrifft die anwendungsspezifischen Aspekte der Objekt- und Attributbildung, Abgrenzung und Interpretation. Dies entspricht dabei der höchsten technischen Abstraktion und tangiert dadurch in erster Linie die kognitive Managementebene eines Operators.
- 6.2 Aspekte der Semantischen
Interaktion
Das zentrale Element der semantischen Interaktion liegt im funktionalen Modell. Dieses stützt sich auf eine fest abgegrenzte, geometrisch tangierte Teilaufgabe und dessen konzeptuelle Methode. Deren Algorithmik wird von der Metrik wie die geometrisch-strukturellen Kompo-nente beeinflußt. Damit verbunden ist die morphologische Fragestellung nach der Zielstruktur oder der durch die Analyse verursachte strukturelle Veränderung oder Anpassung, die aus dem funktionalen Modell resultiert. Ein weiterer Aspekt ist der kognitive thematisch-attributive Aspekt und betrifft auf funktioneller Ebene in erster Linie die Attributerfassung, Aktualisierung oder Übertragung.
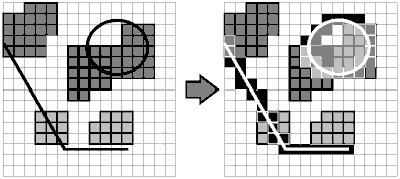
In Abb. 6 findet eine hybride semantische Überlagerung statt. Die strukturell-geometrische Problematik der Berührungspixel und deren Klassifikation fließt in die Attributverarbeitung mit ein. Durch die Klassifikation der Subpixel nach unterschiedlichen Ansätzen besteht die Möglich-keit, diese Aufgliederung in die Attributie-rung und Objektbildung miteinfließen zu lassen. Auf der einen Seite kann dies die qualitativen Wertschöpfung anheben, kann aber auch zu einer Unüberschaubarkeit der Daten führen. Durch die Integration der Subpixelklassifikation können Ansätze der Unschärfebehandlung realisiert werden.
7 Ein Anwendungsbeispiel für die
Integration der hybriden Analyse
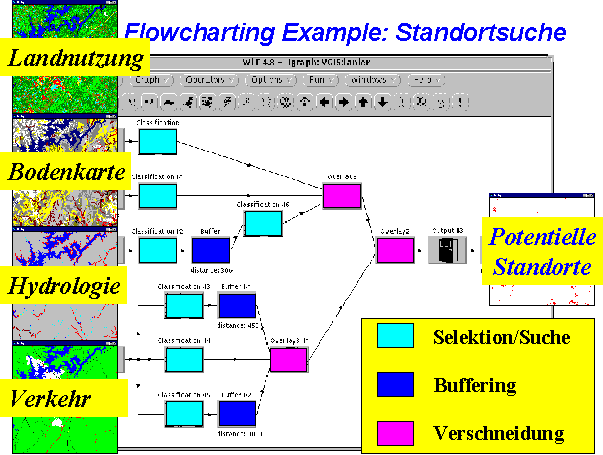
In Abb. 7 wird ein kognitiver Ansatz zur Fest-legung eines räumlichen Analyseprozesses dargestellt: Der Prozeßdesign erfolgt auf einer graphischen Programmieroberfläche als Workflow (hier ein VGIS-Prototyp). Die Daten wie die Operatoren werden dabei auf semantischer Ebene durch Metadaten selektiert und zu einem Prozeßgraphen kombiniert. Im Beispiel werden für eine Standortanalyse Landnutzungsdaten, geologische und hydrologische Daten sowie Verkehrsinformationen verwendet. Durch die logische Aneinanderreihung und Verknüpfung unterschiedlicher funktionaler Modelle als Operatoren erhält man als Resultat ein Gebietsmaske mit den potentiellen Standorten.
In einem solchen Beispiel kommt die Hybridität der Operatoren dann zum Tragen, wenn die ausgewählten Daten, welche auf dieser graphischen Managementebene durch ihre inhaltliche Semantik ausgewählt worden, aufgrund ihrer unterschiedliche Strukturen in Raster- und Vektorformat hybrid prozessiert werden müssen. Zum Beispiel können die Verkehrs- und Geologiedaten aus einer Vektordatenbank stammen, die Landnutzungsdaten aus einer aktuel-len Fernerkundungsauswertung und die hydrologische Daten aus einer kombinierten Datenbank stammen.
8 Schlußbetrachtung und Ausblick
Die hybride Analyse ist Bestandteil der räumlichen Analyse und behandelt die simultane Vektor-Raster- oder Raster-Vektor-Interaktion, ohne dabei eine Konversion vornehmen zu müssen. Viele Prinzipien einer Raster-Vektor- oder Vektor-Raster-Konvertierung betreffen dieselbe Problematik der hybriden Metrikräume, denn es betrifft dieselben geometrischen Primitiven und Strukturen. Die Analyse besitzt jedoch eine erweiterte semantische wie funktionale Dimension. Im Gegensatz der Konversion, welche ein Wechsel der Struktur beinhaltet, sind bei der hybriden Funktionalität die gegenseitige Beeinflussung beider Strukturräume essentiell. Die Kernproblematik liegt dabei in der Abbildung der funktionalen Modelle auf die hybriden Struktur sowie das Zusammenführen unterschiedlichen Metriken zu deren optimierten Nutzung. Diese Funktionalität soll für eine kognitive Benutzerführung in "High-Level-Analytische-GIS-Operatoren" eingebunden werden.
Die hier gezeigten Ansätze und Problemfelder der hybriden Analyse finden bisher kaum Anwendung, weil bis jetzt die hybride Strukturen fehlten und eine leistungsfähige und operationale Algorithmik noch zu entwerfen ist.
Referenzen
Albrecht 1996 - Albrecht, Jochen: Universal Analytical GIS Operations: a task-oriented systematisation of data structure-independent GIS functionality leading towards a geographic modelling lan-guage. PhD-Thesis, ISPA Mitteilungen 23, University of Vechta,1996.
Behr 1998 - Behr, Franz-Josef; Strategisches GIS-Management, Grundlagen und Schritte zur Systemeinführung; Wichmann Verlag, Heidelberg 1998.
Fischer et al. 1996 - Fischer M., Scholten H. J., Unwin D. (ed.): Spatial Analytical Perspectives on GIS; GISDATA IV, Taylor & Francis, London 1996.
Fortheringham/Rogerson 1994 - Fortheringham S., Rogerson P. (ed.): Spatial Analysis and GIS; Taylor and Francis, London 1994.
Glemser/Fritsch 1998 - Glemser M., Fritsch D.: Data Uncertainty in a Hybrid GIS; In: “GIS Between Visions and Applications”, ISPRS Commission IV Symposium, Sept. 7-10, 1998, Stuttgart, Vol 32/4.
Longley/Batty 1996 - Longley P. and Batty M. (ed.): Spatial Analysis: Modelling in a GIS Environment. GeoInformation Inter-national, Cambridge 1996.
OGC 1996 - The OpenGIS Guide: Introduction to Interoperable Geoprocessing, OpenGIS TC Document Number 96-001. Open GIS Consortium: Wayland, MA. Document Number 96-001
Tomlin, 1990 - Tomlin, C. Dana: Geographic Information Systems and Cartographic Modeling. Englewood Cliffs, Prentice Hall.
Voser 1998a - Voser, Stefan A.: Schritte für ein automatisiertes Koordinatensystemmanagement in GIS und Kartographie. Nachrichten aus dem Karten- und Vermessungswesen, Reihe I, Heft Nr. 118, S. 111-125. Bundesamt für Kartographie und Geodäsie, Frankfurt am Main (1998).
Voser et al. 1998b Voser, Stefan A., Jung S.: Towards Hybrid Analysis - Specification of High Level Analytical GIS Operators, Proceedings to the first AGILE-Conference, 23.-25.-April 1998, ITC, Enschede (NL), ITC-Publications, in press.
MapRef - © by Stefan A. Voser; Last Update: 28. October 2001