SCICOS
Este documento describe ejemplos realizados con el programa Scicos(Scilab Connected
Object Simulator),utilizado en el modelado y
simulación de sistemas dinamicos hibridos, Scicos incluye un editor grafico con el cual se puede
construir modelos complejos interconectando bloques los cuales representan
funciones basicas predefinidas en una biblioteca(palettes),
,a lo largo de este documento,el lector podra
realizar los mismos ejemplos que simulan diferentes sistemas matematicos , presentes en diversos campos de la ciencia y
la tecnologia.
Forma de entrar en Scicos.
Abrimos scilab-3.0 luego de lo cual aparece la siguiente ventana
___________________________________________
scilab-3.0
Copyright (c) 1989-2004
Consortium Scilab
(INRIA, ENPC)
___________________________________________
Startup execution:
loading initial environment
-->
y escribimos scicos();
,hacemos enter y aparece la ventana de Scicos.
Sistemas lineales.
Simulación de circuitos electricos.
Asi como los automóviles y
otros objetos con masa arrancan despacio y se aproximan a su velocidad estable
en forma gradual,la
corriente se inicia gradualmente en un circuito inductivo.La
corriente empieza a incementarse tan pronto se aplica
una tension,se incrementa rapidamente
al principio y de ahí mas y mas despacio hasta que se aproxima al valor
estacionario.
Dado el siguiente circuito,
Concideremos la excitación es en
forma de escalon,
realizaremos la simulacion usando la ecuación del circuito que es una ecuacion diferencial de primer orden, v(t)=i(t).R+L.(di(t)/dt) ,
di(t)/dt=(1/L).[v(t)-i(t).R]
en esta ultima expresion hay dos sumados
en el segundo miembro,por lo tanto conectamos dos
entradas a un sumador y la salida de este la multiplicamos por (1/L)
obteniendose di(t)/dt,a continuación
integramos teniendo como resultado i(t),siendo v(t)=10.u(t)
Podemos
obtener la misma respuesta estudiando este documento: http://mathinsite.bmth.ac.uk/html/applets.html#lrseriesAnchor
http://mathinsite.bmth.ac.uk/pdf/lrseries_theory1.pdf
Simulación
de un circuito resistencia-capacidad.
La siguiente ecuación diferencial
ky’+y=x
se presenta en procesos termicos y electricos ,como en el
siguiente ejemplo ,que es un circuito,donde e1(t) es la
excitación en forma de escalon,
dibujo 1
y’=(1/k)[x-y] ,
en esta ultima expresion hay
dos sumados en el segundo miembro,por lo tanto
conectamos dos entradas a un sumador y la salida de este la multiplicamos por (1/k)
obteniendose y’,a continuación
integramos teniendo como resultado y.
dibujo 2
si deseamos simular el circuito del dibujo 1 ,es e2’=(1/RC)[e1-e2] (3) ,con x= e1 y y=
e2 ,luego 1/k=1/RC
,
R=1000 ohm C=0. 0001
faradios ,1/k=10.
La
simulación resulta,
se obtiene el mismo resultado con el simulador de circuitos SPICE,
Modelado de
una ecuación diferencial de segundo orden con coeficientes constantes.
Dada
la ecuacion diferencial de segundo orden con
coeficientes constantes,cuyo
analisis el lector puede consultar en Sistema lineal de
segundo orden.
Se quiere modelar el sistema,que
simule esta ecuacion mediante bloques interconectados,para ello hacemos,
y”=
100-1.2y’-16.36y (5)
hay tres sumados en el segundo miembro de la ultima ecuación,por lo tanto conectamos tres entradas al sumador compuesto,rotulando cada entrada
con el sumando correspondiente del segundo miembro de la ecuación,la
salida y’’ se aplica al
integrador obteniendose y’,si
se integra nuevamente se obtiene y
,la variable y’ se la multiplica por 1.2 y se aplica a una
entrada del sumador el cual modifica su signo y a la variable y
se la multiplica por 16.36 y se la aplica al sumador,
Realizando la simulacion resulta,
Parametros de los bloques.
Es
importante ajustar los parametros de los bloques para
obtener resultados acordes al sistema estudiado,el primero en ser modificado sera
el Clock,para este caso hacemos
Period
: 0.01
Init time : 0
Este
tiempo Period : 0.01,lo genera este bloque el cual en este caso activa el
bloque Scope y seria como si fuera un sistema de
muestreo con la unica diferencia que el valor
introducido sera presentado el resto lo une con una recta,pruebe el lector hacer Period : 1 y vera
como los puntos verdaderos son unidos por rectas y aun el ultimo grafico no es
un trazo continuo.
Entrando
en el menú a Set Block properties que esta en Simulate ,hacemos Final Inegration time : 10 , esto hara
que la simulación termine para un tiempo 10.
Estudio
de algunos puntos en el grafico.
En el
documento Sistema
lineal de segundo orden.,vimos que el resultado de
la ecuación diferencial es
y(x)=
6.112 {1- e^(-0.6t)
[cos(4t) +0.15 sin(4t)]}
si la representamos con algun programa que dibuje la funcion,por
ejemplo con Scilab o con Graphmatica,podremos
comparar los resultados obtenidos,el siguiente
grafico realizado con Graphmatica ,fue ampliado en el primer “pico” ,para ser
comparado con lo obtenido con Scicos,
y la simulacion resulto,(este grafico se va
obteniendo utilizando el aumento +)
de Graphmatica vemos que las oscilaciones
terminan en un tiempo 9 luego de realizar 5 oscilaciones(aproximadamente) como
el grafico de la simulacion,
La siguiente simulación se obtuvo con Final Inegration
time : 1 y en Set Scope Parameters Ymin=-1 y Ymax=1 y con esto
verificamos el punto inicial (0,0),
Ley de enfriamiento de Newton.
De acuerdo a la ley de enfriamiento de Newton,la variación de la temperatura con el tiempo T(t)
de un cuerpo inmerso en un medio a temperatura constante A,es proporcional a la diferencia T-A ,esto
es
(6)
siendo k
una constante,supongamos que k=-0.1 y que y(0)=50 y A=10
, en este caso y’=k(T-A),luego el sistema sera,
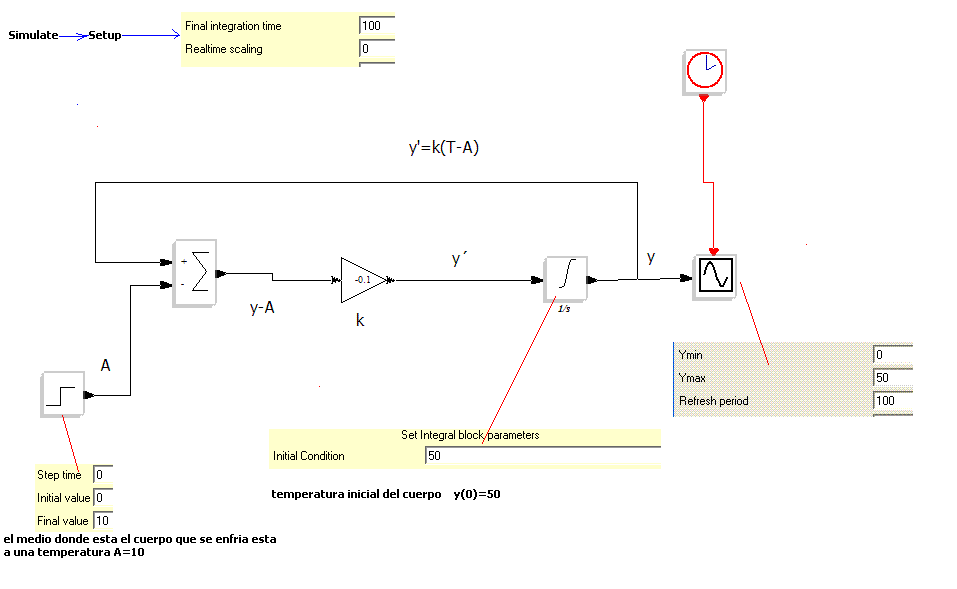
realizando la simulacion,
La solucion de esta ecuacion
diferencial es T(t)=A+(T(0)-A).e^(k.t)
,si la representamos con Graphmatica es,
Branching.
En el siguiente ejemplo se usa un bloque tomado del conjunto denominado branching,donde se resalta la influencia de los sistemas electronicos en la definición de los bloques,en
este caso los pulsos del generador clock son
transmitidos por medio de una llave controlada al scope(osciloscopio),dos
generadores de señales senoidales s1 y s2 activan al sistema,s1 se aplica al comparador ,si esta señal es mayor
que cero if in>0
,la llave conmuta a la salida then,es decir el
osciloscopio se dispara y por lo tanto presenta las señales cuando s1>0 como
se ve en los graficos,cuando s1 es negativa no hay
señales presentadas
Sistemas
no lineales.
Simulación
de un relay.
El relay
es un componente muy utilizado en sistemas de control,el siguiente sistema es una simulación donde el
mismo tiene a su entrada una señal que aumenta linealmente en el tiempo,hasta que llega a un valor sl=1
que hace que actue,es decir la señal sr pasa de 0 a 1.
Eduardo Ghershman, 23.2.2005