TRANSFORMAÇÃO DE COORDENADAS ORBITAIS POLARES HELIOCÊNTRICAS
PARA
EQUATORIAIS ESFÉRICAS GEOCÊNTRICAS
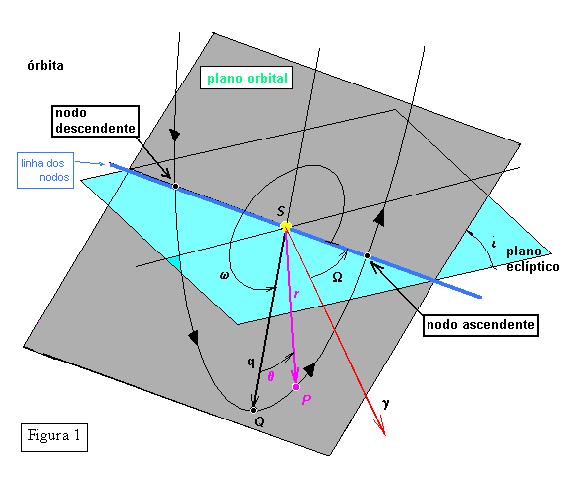
A posição do astro na sua órbita num determinado instante está definida pelo ponto P, cujas coordenadas polares heliocêntricas, tomando como eixo de referência a linha SQ do periélio, são r e q .
FORMA VETORIAL DAS COORDENADAS ORBITAIS:
COORDENADAS HELIOCÊNTRICAS ORBITAIS RETANGULARES
De acordo com a figura 1 podemos transformar as coordenadas polares P ( r, q ) em retangulares orbitais heliocêntricas (ou seja o ponto P referido a uma terna xyz), colocando o eixo x coincidindo com a linha do periélio SQ. O plano orbital do astro fica então contido no plano xy, e o eixo z, perpendicular ao orbital xy. Neste caso o problema se reduz apenas às conhecidas fórmulas:
Resulta mais interessante porém,
expressar estas coordenadas em forma vetorial, isto é,
o vetor posição
, representado por uma matriz de 3 x 1:
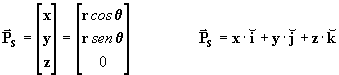
FORMA VETORIAL DAS COORDENADAS ECLÍPTICAS:
COORDENADAS HELIOCÊNTRICAS ECLÍPTICAS RETANGULARES
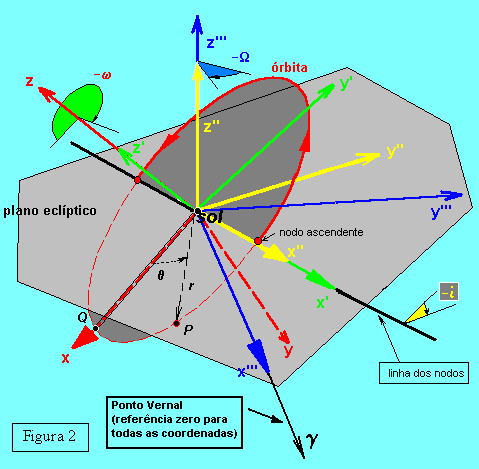
Na figura 2 observamos a posição do ponto P
referido a terna xyz
própria da órbita. Em vermelho temos a órbita
do astro em seu respectivo plano (cinza obscuro). Na figura, o plano orbital corta o
plano eclíptico (cinza claro) determinando a linha dos nodos.
A terna própria do plano eclíptico é a
xyz;
e o que nós queremos é referir o vetor
a esta terna eclíptica. Ë
necessário fazermos então uma transformação de coordenadas.
O processo de transformação de coordenadas exige
então referirmos o vetor
(inicialmente no sistema xyz
), no sistema x’’’y’’’z’’’
. Para isto faremos uma rotação levando o eixo
de referência inicial x
a coincidir com o eixo
x’’’ .
Porém esta rotação complexa pode ser decomposta numa série
de rotações sucessivas, segundo o seguinte esquema:
(
xyz ) ® (x’y’z’) ® (x’’ y’’ z’’) ® (x’’’y’’’z’’’)Logo temos três transformações (giros):
Þ
Genericamente podemos definir então uma transformação Ab
( que representa um giro de ângulo b
num dos eixos) tal que o vetor 
referido à terna inicial, terá no novo sistema girado, coordenadas 
.
A fórmula de transformação de coordenadas para este caso será então:
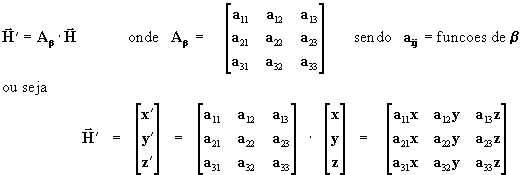
Para o nosso problema, e considerando mais de uma transformação, temos os ângulos -
, -i
, -W
, portanto, as matrizes valem:
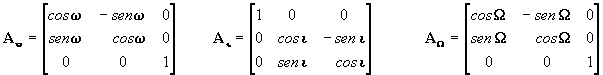
Ou seja que no nosso caso:
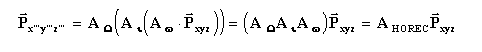
Fazendo então a multiplicação das três matrizes obtemos:
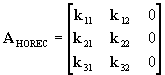
Os coeficientes desta matriz para converter retangulares orbitais em ret. eclípticas são:
Esta matriz é extremadamente importante pois nos permite calcular, por exemplo, a posição dos planetas do sistema solar referida ao plano eclíptico (valores x’’’ e y’’’). Graficando estes valores obtemos a imagem do sistema solar tal como se fosse visto desde o pólo norte eclíptico.
COORDENADAS HELIOCÊNTRICAS ECLÍPTICAS POLARES ESFÉRICAS
As coordenadas heliocêntricas eclípticas
retangulares são muito importantes pois permitem calcular as denominadas
coordenadas heliocêntricas eclípticas polares esféricas
, ou seja: o raio vetor ( r ),a longitude
eclíptica ( l
) e a latitude eclíptica ( b
), com valores tal que 0°
l
360°
e -90°
b
+90°
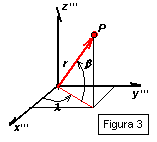
, como pode ser visto na figura 3.
Segundo a mesma figura 3, se denominamos r’
a projeção de r no plano xy, então:
Logo:
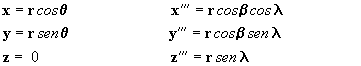
Como 
(é invariante às transformações)
, observando a figura 3 resulta podemos definir os cosenos diretores
l, m, n do vetor
:
e como
resulta então:
360°
e -90°
b
+90°
porém não é difícil deduzir que: 
logo, como W
, i
, w
e q
são valores conhecidos, podemos obter l
da equação anterior, que introduzido na seguinte fórmula nos dá b
: 
É interessante observar que si q = 0 então l = lp (longitude do periélio), ou seja:
COORDENADAS GEOCÊNTRICAS ECLÍPTICAS RETANGULARES
Agora nós temos o vetor do astro
referido ao sol e o vetor
da Terra, também referido ao sol.
Como podemos observar na figura 4, o vetor que define a posiçã
o geocêntrica em coordenadas geocêntricas eclípticas
retangulares é o vetor 
.
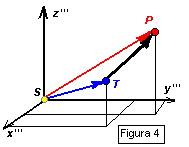
Resulta óbvio que: PS = TS + PT {heliocêntrico}
Þ PT = PS - TS {geocêntrico}
ou seja:
{geocêntrico)
quer dizer que a diferença (para o instante dado) entre as coordenadas heliocêntricas eclípticas retangulares do astro e as coordenadas heliocêntricas retangulares da Terra nos proporciona as coordenadas geocêntricas eclípticas retangulares do astro em questão.
O que resta agora e fazermos a transformação de eclípticas para
equatoriais; para isto devemos girar o eixo de referência x’’’
(direção do Ponto Vernal -
g ) um ângulo -
, onde
é o valor da inclinação da eclíptica terrestre
( 23°
27¢
).
COORDENADAS GEOCÊNTRICAS EQUATORIAIS RETANGULARES
Tal como foi dito, o vetor
referido ao plano eclíptico, deve ser agora referido ao plano equatorial.
Fazemos isto mediante a transformação
tal que :
e
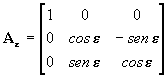
logo:
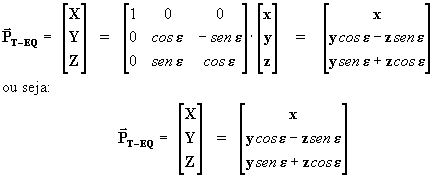
logo, a distância do planeta à Terra será:
COORDENADAS GEOCÊNTRICAS EQUATORIAIS ESFÉRICAS
A posição do astro é definida normalmente, do ponto de vista geocêntrico, em coordenadas polares esféricas, ou seja, o raio vector e dois ângulos. De acordo com a figura 5, as coordenadas polares esféricas geocêntricas são: P ( rT, a , d ), onde a é a ascensão reta e d é a declinação do astro P.
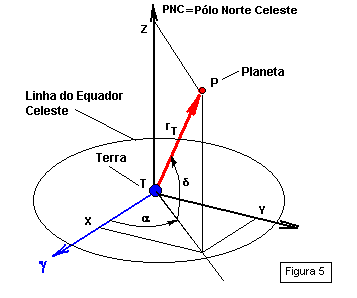
É fácil observar que a projeção de rT no plano XY vale 
. Logo :
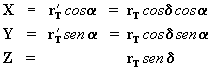
e
Podemos definir os cosenos diretores l, m, n do vetor 
:
logo:
Como 0°
a
0 
360°
e -90°
+90°
,a determinação do quadrante se faz segundo a seguinte regra:
Entretanto, os valores retornados de a
pela função Arctan estão em graus sexagesimais, e a
é dada em horas, devemos fazer a
[°
] / 15 para obtermos a
[h]. Pois 15°
= 1 hora para a Terra. O valor de a
[h] está em horas decimais (ex. 1.25 h = 1h 15m) e não em horas sexagesimais [h m s]. Portanto temos que 0 h. a
0 24 h. e -90°
+90°
.
Assim, as coordenadas geocêntricas equatoriais esféricas são: a
, e rT.
