The Past Master Club
LISP.LSP
;;;;;;;;;;;;;;;;;;;; START.BAT ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
--c:\n\nic4\lisp.bat--
@echo off
set lispstack=15000
set lispheap=30000
lisp\lisp lisp\init.lsp
set lispstack=
set lispheap=
;;;;;;;;;;;;;;;;;;;;;;;;;; INIT ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
--c:\n\nic4\lisp\init.lsp--
(unless (fboundp 'strcat)
(defun strcat (&rest str)
(apply #'concatenate 'string str))
)
(defun sp()(princ " "))
(defun nl()(terpri))
(defun pa()(do((i 1(1+ i)))((> i 24))(nl)))(pa)
(defun o()(exit))
(defun i()(load "lisp\\init"))
(defun type(x)(setq f(open x))(do((i 0(1+ i)))((eq i 'eof))
(princ(read-line f))(nl)
))
(setq ot 't zp 0 ts 0)
(defun tm()
(when ot
(setq z (-(/(get-internal-run-time) internal-time-units-per-second)zp))
(setq z1 (- z ts))
(setq ts z)
(setq i(truncate z 3600))
(setq z(- z (* 3600 i)))
(setq j(truncate z 60))
(setq z(- z -0.5 (* 60 j)))
(setq w(truncate z 1))
(setq y1(truncate z1 60))
(setq z1(- z1 -0.5 (* 60 y1)))
(setq z1(truncate z1 1))
(format t "~1,54tTIME ~d:~2,d:~2,d <<~2,@d~a~2,d~a>> "
i j w y1 "'" z1 (int-char 34))
))
; print in lower case
(setq *print-case* :downcase)
(pa)
(load "lisp\\cal")
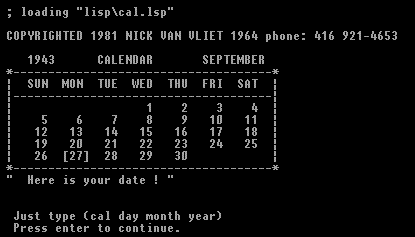
(nl)(princ " Just type (cal day month year)")
(nl)(princ " Press enter to continue.")
(read-line)
(pa)
(load "lisp\\hanoi")
(nl)(princ " Just type (hanoi #)")
(nl)(princ " Press enter to continue.")
(read-line)
(pa)
(load "lisp\\lgg")
(nl)(princ " Just type (lgg)")
(nl)(princ " Press enter to continue.")
(read-line)
(pa)
(load "lisp\\crpath")
(nl)(princ " Just type (path) or (exit)")
;;(nl)(princ " Press enter to continue.")
;;(read-line)
(setq zp 0)(tm)(setq zp ts)
;;(pa)
;;;(load "lisp\\spiral")
(nl)(princ " Press enter to continue.")
(read-line)
(pa)
(load "string.lsp")
(nl)(princ " Just type (tst) or (exit)")
(nl)(princ " Do you wish to exit or ctrl C to do examples?")
(read-line)
(o)
;;;;;;;;;;;;;;;;;;;;;;;; cal.lsp ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
 --c:\n\nic4\lisp\cal.lsp--
(defun cal (dy mn yr) ;;SAME CALENDAR PROGRAM AS IN GWBASIC
(setq rs '((0 "M")(1 "A")(2 "B")(3 "C")(4 "K")(5 "F")(6 "G")
(7 "A")(8 "I")(9 "D")(10 "E")(11 "F")(12 "N")(13 "B")
(14 "C")(15 "D")(16 "L")(17 "G")(18 "A")(19 "B")(20 "J")
(21 "E")(22 "F")(23 "G")(24 "H")(25 "C")(26 "D")(27 "E"))
)
(setq ys '((1 31 "JANUARY ")(2 28 "FEBRUARY ")(3 31 "MARCH ")
(4 30 "APRIL ")(5 31 "MAY ")(6 30 "JUNE ")
(7 31 "JULY ")(8 31 "AUGUST ")(9 30 "SEPTEMBER")
(10 31 "OCTOBER ")(11 30 "NOVEMBER ")(12 31 "DECEMBER "))
)
(setq ms(cddr(assoc mn ys)))
(terpri)
(princ "COPYRIGHTED 1981 NICK VAN VLIET 1964")
(terpri)(terpri)
(princ " ")(princ yr)(princ " ")(princ " CALENDAR ")
(princ (car ms))(princ " ")
(terpri)(princ "*-------------------------------------*")
(terpri)(princ "| SUN MON TUE WED THU FRI SAT |")
(terpri)(princ "|-------------------------------------|")
(cond ((= yr 1800) (setq yr 1902))
((= yr 1900) (setq yr 1906))
((< yr 1900) (setq yr (+ 12 yr)))
(t nil)
)
(setq ly (rem yr 4))
(setq rm (rem yr 28))
(setq dm(cadr(assoc mn ys)))
(setq rl (cadr (assoc rm rs)))
(if (= mn 2) (if (= ly 0) (setq dm (+ dm 1))))
(cond ((= mn 1) (setq g 0))
((= mn 10)(setq g 0))
((= mn 5) (setq g 1))
((= mn 8) (setq g 2))
((= mn 2) (setq g 3))
((= mn 3) (setq g 3))
((= mn 11)(setq g 3))
((= mn 6) (setq g 4))
((= mn 9) (setq g 5))
((= mn 12)(setq g 5))
((= mn 4) (setq g 6))
((= mn 7) (setq g 6))
(t nil)
)
(if (= ly 0)
(cond((= mn 1)(setq g (- g 1)))
((= mn 2)(setq g (- g 1)))
(t nil)
)
)
(cond((equal rl "A")(setq g (+ g 0)))
((equal rl "N")(setq g (+ g 0)))
((equal rl "B")(setq g (+ g 1)))
((equal rl "H")(setq g (+ g 1)))
((equal rl "C")(setq g (+ g 2)))
((equal rl "I")(setq g (+ g 2)))
((equal rl "D")(setq g (+ g 3)))
((equal rl "J")(setq g (+ g 3)))
((equal rl "E")(setq g (+ g 4)))
((equal rl "K")(setq g (+ g 4)))
((equal rl "F")(setq g (+ g 5)))
((equal rl "L")(setq g (+ g 5)))
((equal rl "G")(setq g (+ g 6)))
((equal rl "M")(setq g (+ g 6)))
(t nil)
)
(setq g (+ g 7))(setq g (+ (rem g 7) 1))
(setq n 1)
(do ((h 1(+ h 1)))((> h 6))
(terpri)(princ "|")
(if(= n 1)
(if(= h 1)
(if(/= g 1)
(do ((i 1(+ i 1)))((>= i g))
(princ " ")
)
)
)
)
(do ((j 1(+ j 1)))((> j 7))
(if (= n 1)(if (= h 1) (setq j g)))
(if(= n (+ dy 1))(princ "]")(princ " "))
(princ " ")
(if (< n 10) (princ " "))
(if (= n dy)(princ "[")(princ " "))
(if (<= n dm)(princ n)(princ " "))
(setq n (+ n 1))
)
(princ " |")
(if (> n dm)(setq h 10))
)
(terpri)
(princ "*-------------------------------------*")
(terpri)
(print " Here is your date ! ")
(terpri)
)
(cal '27 '9 '1943)
;;;;;;;;;;;;;;;;;;;;; hanoi.lsp ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
--c:\n\nic4\lisp\cal.lsp--
(defun cal (dy mn yr) ;;SAME CALENDAR PROGRAM AS IN GWBASIC
(setq rs '((0 "M")(1 "A")(2 "B")(3 "C")(4 "K")(5 "F")(6 "G")
(7 "A")(8 "I")(9 "D")(10 "E")(11 "F")(12 "N")(13 "B")
(14 "C")(15 "D")(16 "L")(17 "G")(18 "A")(19 "B")(20 "J")
(21 "E")(22 "F")(23 "G")(24 "H")(25 "C")(26 "D")(27 "E"))
)
(setq ys '((1 31 "JANUARY ")(2 28 "FEBRUARY ")(3 31 "MARCH ")
(4 30 "APRIL ")(5 31 "MAY ")(6 30 "JUNE ")
(7 31 "JULY ")(8 31 "AUGUST ")(9 30 "SEPTEMBER")
(10 31 "OCTOBER ")(11 30 "NOVEMBER ")(12 31 "DECEMBER "))
)
(setq ms(cddr(assoc mn ys)))
(terpri)
(princ "COPYRIGHTED 1981 NICK VAN VLIET 1964")
(terpri)(terpri)
(princ " ")(princ yr)(princ " ")(princ " CALENDAR ")
(princ (car ms))(princ " ")
(terpri)(princ "*-------------------------------------*")
(terpri)(princ "| SUN MON TUE WED THU FRI SAT |")
(terpri)(princ "|-------------------------------------|")
(cond ((= yr 1800) (setq yr 1902))
((= yr 1900) (setq yr 1906))
((< yr 1900) (setq yr (+ 12 yr)))
(t nil)
)
(setq ly (rem yr 4))
(setq rm (rem yr 28))
(setq dm(cadr(assoc mn ys)))
(setq rl (cadr (assoc rm rs)))
(if (= mn 2) (if (= ly 0) (setq dm (+ dm 1))))
(cond ((= mn 1) (setq g 0))
((= mn 10)(setq g 0))
((= mn 5) (setq g 1))
((= mn 8) (setq g 2))
((= mn 2) (setq g 3))
((= mn 3) (setq g 3))
((= mn 11)(setq g 3))
((= mn 6) (setq g 4))
((= mn 9) (setq g 5))
((= mn 12)(setq g 5))
((= mn 4) (setq g 6))
((= mn 7) (setq g 6))
(t nil)
)
(if (= ly 0)
(cond((= mn 1)(setq g (- g 1)))
((= mn 2)(setq g (- g 1)))
(t nil)
)
)
(cond((equal rl "A")(setq g (+ g 0)))
((equal rl "N")(setq g (+ g 0)))
((equal rl "B")(setq g (+ g 1)))
((equal rl "H")(setq g (+ g 1)))
((equal rl "C")(setq g (+ g 2)))
((equal rl "I")(setq g (+ g 2)))
((equal rl "D")(setq g (+ g 3)))
((equal rl "J")(setq g (+ g 3)))
((equal rl "E")(setq g (+ g 4)))
((equal rl "K")(setq g (+ g 4)))
((equal rl "F")(setq g (+ g 5)))
((equal rl "L")(setq g (+ g 5)))
((equal rl "G")(setq g (+ g 6)))
((equal rl "M")(setq g (+ g 6)))
(t nil)
)
(setq g (+ g 7))(setq g (+ (rem g 7) 1))
(setq n 1)
(do ((h 1(+ h 1)))((> h 6))
(terpri)(princ "|")
(if(= n 1)
(if(= h 1)
(if(/= g 1)
(do ((i 1(+ i 1)))((>= i g))
(princ " ")
)
)
)
)
(do ((j 1(+ j 1)))((> j 7))
(if (= n 1)(if (= h 1) (setq j g)))
(if(= n (+ dy 1))(princ "]")(princ " "))
(princ " ")
(if (< n 10) (princ " "))
(if (= n dy)(princ "[")(princ " "))
(if (<= n dm)(princ n)(princ " "))
(setq n (+ n 1))
)
(princ " |")
(if (> n dm)(setq h 10))
)
(terpri)
(princ "*-------------------------------------*")
(terpri)
(print " Here is your date ! ")
(terpri)
)
(cal '27 '9 '1943)
;;;;;;;;;;;;;;;;;;;;; hanoi.lsp ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
 --c:\n\nic4\lisp\hanoi.lsp--
(defun hanoi(i)
(defun han(n x y z)
(if(>(- n 1)0)(han (- n 1) x z y))
;; (terpri)(princ "From ")(princ x)(princ " to ")(princ z) ;old method
(format t "\n From ~a to ~a" x z)
(if(>(- n 1)0)(han (- n 1) y x z))
)
(han i 'Peg1 'Peg2 'Peg3)
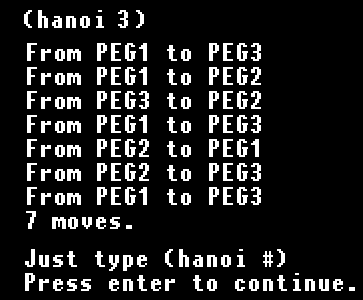
(terpri)(princ (-(expt 2 i)1))(princ " moves.")(terpri)
)
(hanoi 3)
;;;;;;;;;;;;;;;;;;;;;;; lion/goat/grain.lsp ;;;;;;;;;;;;;;;;;;;
--c:\n\nic4\lisp\hanoi.lsp--
(defun hanoi(i)
(defun han(n x y z)
(if(>(- n 1)0)(han (- n 1) x z y))
;; (terpri)(princ "From ")(princ x)(princ " to ")(princ z) ;old method
(format t "\n From ~a to ~a" x z)
(if(>(- n 1)0)(han (- n 1) y x z))
)
(han i 'Peg1 'Peg2 'Peg3)
(terpri)(princ (-(expt 2 i)1))(princ " moves.")(terpri)
)
(hanoi 3)
;;;;;;;;;;;;;;;;;;;;;;; lion/goat/grain.lsp ;;;;;;;;;;;;;;;;;;;
 --c:\n\nic4\lisp\lgg.lsp--
(defun lgg()
(defun gt(n x y z v w)
(terpri)(princ "Row to the right: ")(princ z)
(if (>(- n 1)0)
(progn
(princ " and row back: ")(princ w)
(gt (- n 1) z x y w v)
)
)
)
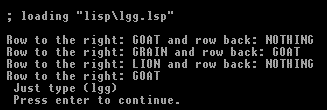
(gt 4 'Lion 'Grain 'Goat 'Goat 'nothing)
)
(lgg)
;;;;;;;;;;;;;;;;;;;;;;; critical path.lsp ;;;;;;;;;;;;;;;;;;;;;;
--c:\n\nic4\lisp\lgg.lsp--
(defun lgg()
(defun gt(n x y z v w)
(terpri)(princ "Row to the right: ")(princ z)
(if (>(- n 1)0)
(progn
(princ " and row back: ")(princ w)
(gt (- n 1) z x y w v)
)
)
)
(gt 4 'Lion 'Grain 'Goat 'Goat 'nothing)
)
(lgg)
;;;;;;;;;;;;;;;;;;;;;;; critical path.lsp ;;;;;;;;;;;;;;;;;;;;;;
--c:\n\nic4\lisp\crpath.lsp--
(defun path () ;;SAME PROGRAM AS IN GWBASIC
(defun rl()(nl)(read-line))
(defun sp()(princ " "))
(defun nl()(terpri))
(defmacro while (test &rest forms) `(do () ((not ,test)) ,@forms))
(if (not (fboundp 'unless))(defmacro unless (test &rest forms)`(if (not ,test)
`(progn ,@forms)))
)
(unless (fboundp 'strcat)(defun strcat (&rest str)
(apply #'concatenate 'string str))
)
(defun mmp(x y)(setq zz nil)(do ((i 0 (1+ i)))((> i (- (length y) 1)))
(when (eq x (char y i))(setq zz 't i ks)))(setq zz zz)
);z=z-NEC!
(defun intgrql (x y) ;A=B*INT A/B =ba/b=a
(if (= x (* y (truncate x y)))(setq z 1)(setq z 0))
)
(defun mmbrp(x y)(setq z nil)(cond((= x (car y))(setq z 't))
((cdr y) (mmbrp x (cdr y)))(t (setq z nil)))(setq z z)
)
;************ ARRAY (k^2+SPARE) *********
(setq k 12 n (+ k 1) l (- k 1) kk (* n n))
(setq grdt (make-array kk)) ;array T
(setq grdo (make-array kk)) ;array O
(setq grdp (make-array kk)) ;array P
(setq grds (make-array kk)) ;array S
(setq grdy (make-array kk)) ;array Y
(setq grde (make-array kk)) ;array E
(setq grdz (make-array kk)) ;array Z
;*******************************************
(defun sum(x y)(+(*(- x 1)k)(- y 1)))
(defun rest (file x y)
(do ((h 1 (1+ h)))((> h x))
(do ((i 1 (1+ i)))((> i y))
(setf (aref file (sum h i)) 0)
)
)
)
(rest grdt n k)(rest grdo n k)(rest grdp n k)(rest grds n k)(rest grds n k)
(rest grde n k)
(defun elmnt (fil x y tim)
(setf (aref fil (sum x y)) tim)
)
(defun exmpl() ;example Time active array
(elmnt grdt 1 2 8) ;1
(elmnt grdt 1 3 14) ;2
(elmnt grdt 1 4 9) ;3
(elmnt grdt 2 3 4) ;4
(elmnt grdt 2 5 9) ;5
(elmnt grdt 2 6 6) ;6
(elmnt grdt 3 4 7) ;7
(elmnt grdt 3 6 10) ;8
(elmnt grdt 3 8 6) ;9
(elmnt grdt 3 9 9) ;10
(elmnt grdt 4 7 10) ;1
(elmnt grdt 4 8 9) ;2
(elmnt grdt 4 11 6) ;3
(elmnt grdt 5 9 3) ;4
(elmnt grdt 6 7 5) ;5
(elmnt grdt 6 8 3) ;6
(elmnt grdt 6 9 8) ;7
(elmnt grdt 7 11 4) ;8
(elmnt grdt 8 7 8) ;9
(elmnt grdt 8 9 4) ;20
(elmnt grdt 8 10 5) ;1
(elmnt grdt 8 11 13) ;2
(elmnt grdt 9 10 5) ;3
(elmnt grdt 10 12 13) ;4
(elmnt grdt 11 10 6) ;5
(elmnt grdt 11 12 17) ;6
)
(exmpl)
(defun setpop () ;O grid unit T matrix
(do ((h 1 (1+ h)))((> h n))
(do ((i 1 (1+ i)))((> i k))
(unless (=(aref grdt (sum h i))0)
(setf (aref grdo (sum h i)) 1) ;unit matrix
(setf (aref grdp (sum i h)) 1) ;inverse matrix
)
)
(setf (aref grdp (sum h h)) 1) ;inverse matrix ready for DOT PRODUCT
)
)
(setpop) ;grids T,O & P ready
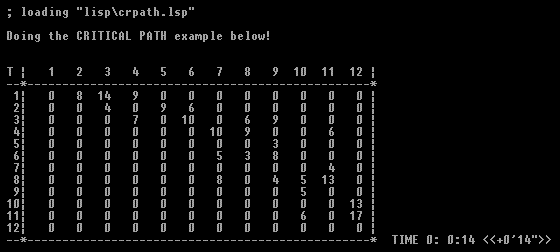
(format t "\nDoing the CRITICAL PATH example below!\n\n")
(defun ln()
(format t "\n--*")
(do ((o 1 (1+ o)))((> o k))
(format t "----")
)
(princ "-*")
)
;******************* SCREEN ****************************
(defun scrn (fil x y) ;display arrays
(princ (int-char 7))
(format t "\n~a |" y)
(do ((h 1 (1+ h)))((> h k))
(format t "~4,d" h)
)
(princ " |")
(ln)
(do ((h 1 (1+ h)))((> h x))
(format t "\n~2,d|" h)
(do ((i 1 (1+ i)))((> i k))
(format t "~4,d" (aref fil (sum h i)))
)
(princ " |")
)
(ln)
(tm)
(nl)
)
(scrn grdt k 'T)
;(scrn grdo k 'O)
;(read-char)
;(scrn grdp n 'P)
;(read-char)
(defun dotprdct() ;O grid unit T matrix
(do ((h 1 (1+ h)))((> h k))
(do ((i 1 (1+ i)))((> i k))
(setq a 0)
(do ((g 1 (1+ g)))((> g k))
(setq a (+ a (* (aref grdp (sum h g))(aref grdp (sum g i)))))
)
(if(= a 0) ;if a dot product than true
(setf (aref grds (sum h i)) 0)
(setf (aref grds (sum h i)) 1)
)
)
)
(do ((h 1 (1+ h)))((> h k))
(do ((i 1 (1+ i)))((> i k))
(setq a 0)
(do ((g 1 (1+ g)))((> g k))
(setq a (+ a (* (aref grds (sum h g))(aref grds (sum g i)))))
)
(if(= a 0) ;again finally if a dot product than true
(setf (aref grdp (sum h i)) 0)
(setf (aref grdp (sum h i)) 1)
)
)
)
(do ((h 1 (1+ h)))((> h k))
(setf (aref grdp (sum n h))h)
)
)(dotprdct)
;(scrn grdp n 'P)
;(nl)(princ "Grid P dotproduct with D.")(nl)
(rest grds n k) ;reset array Y for Y values
(defun loop(v z) ;bb 1 xx 1
(setq cc 1 bb v xx z)
(do ((h 1 (1+ h)))((> h k))
(setq yy 0 aa 0)
(do ((i 1 (1+ i)))((> i k))
(setq ee(aref grdp (sum h i)))
(setq aa (+ aa ee))
(setq f(* aa ee))
(if (= f 1)
(setq yy (aref grdp (sum n i)))
)
)
(when (= aa 1)
(setf (aref grds (sum bb cc))yy)
(setq ii i)
(if(< xx cc)(setq xx cc))
(setq cc(+ cc 1))
(setq i ii)
)
)
(do ((h 1 (1+ h)))((> h (- cc 1)))
(do ((i 1 (1+ i)))((> i k)) ;get i value for Ybc @ a=1
(when (=(aref grds (sum bb h))(aref grdp (sum n i)))
(do ((m 1 (1+ m)))((> m n))
(do ((w i (1+ w)))((> w l))
(setf (aref grdp (sum m w))(aref grdp (sum m (+ w 1))))
)
(setf (aref grdp (sum m k))0)
)
(setq i kk) ;get next Ybc
)
)
)
(setq ab(- bb 1)) ;omit # 12
(setq bb(+ bb 1))
(unless (= aa 0)(loop bb xx))
)(loop 1 1)
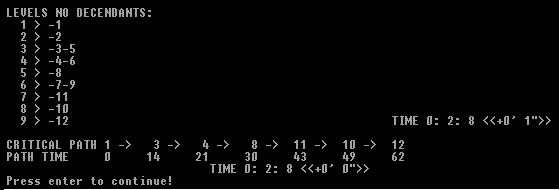
(format t "\nLEVELS NO DECENDANTS: ")
(do ((h 1 (1+ h)))((> h ab))
(format t "\n~3,d ~a "h '>)
(do ((i 1 (1+ i)))((> i xx))
(setq f (aref grds (sum h i)))
(setf (aref grde (sum h i)) f)
(unless (= f 0)
(princ "-")
(princ (aref grds (sum h i)))
)
)
)
(tm)
(nl)
(do ((h 1 (1+ h)))((> h n))
(do ((i 1 (1+ i)))((> i n))
(setf (aref grds (sum h i))(aref grdo (sum h i)))
(setf (aref grdy (sum h i))0)
(setf (aref grdz (sum h i))0)
(setf (aref grdp (sum h i))0)
)
)
(setf(aref grdp (sum n 1))1)
(defun loop2()
(setq bb 0)
(do ((h 1 (1+ h)))((> h k))
(unless (= (aref grdp (sum n h))0)
(do ((i 1 (1+ i)))((> i k))
(unless (and (= (aref grdo (sum h i))0)(= (aref grds (sum h i))0))
(setf (aref grdp (sum h i))(+ (aref grdt (sum h i))
(aref grdp (sum n h))))
(setf (aref grds (sum h i))0)
)
)
)
)
(do ((i 1 (1+ i)))((> i k)) ;vert before horz
(when (= (aref grdp (sum n i))0)
(setq aa 0)
(do ((h 1 (1+ h)))((> h k))
(setq aa (+ aa (aref grds (sum h i))))
)
(setq bb 1)
(when (= aa 0)
(setq bb 0 yy 0)
(do ((h 1 (1+ h)))((> h k))
(setq xx (aref grdp (sum h i)))
(when (> xx yy)
(setf (aref grdy (sum 1 i))h)
(setf (aref grdy (sum 2 i))i)
(setf (aref grdy (sum 3 i))h)
(setf (aref grdy (sum 4 i))i)
(setf (aref grdy (sum 5 i))xx)
(setf (aref grdy (sum 6 i))0)
(setf (aref grdp (sum n i))xx)
(setq yy xx)
)
)
(setq aa 0)
(do ((h 1 (1+ h)))((> h k))
(setq aa (+ aa (aref grds (sum h i)))) ;vert before horz
)
(if (> aa 0)(setq bb 1))
)
)
)
(if(= bb 1)(loop2))
)
(loop2)
(do ((h 1 (1+ h)))((> h 6))
(setf (aref grdy (sum h 1))1)
)
(defun loop3()
(setq bb 0)
(do ((h 1 (1+ h)))((> h l))
(setq aa 0)
(do ((i 1 (1+ i)))((> i k))
(when(=(aref grdy (sum 2 h))(aref grdy (sum 1 i)))(setq aa 1 i kk)) ;vert
)
(unless (= aa 1)
(setq bb 1)
(setf (aref grdy (sum 1 h))0)
(setf (aref grdy (sum 2 h))0)
(setf (aref grdy (sum 5 h))0)
(setf (aref grdy (sum 6 h))0)
(setf (aref grdy (sum 7 h))0)
)
)
(if(= bb 1)(loop3))
)(loop3)
(setq aa 1)
(format t "\nCRITICAL PATH 1")
(setf(aref grde (sum 1 k))1)
(setq cc 2 nk 3)
(defun loop4() ;critical path elements
(do ((h 1 (1+ h)))((> h k))
(do ((i 2 (1+ i)))((> i k))
(when(= aa (aref grdy (sum 1 i)))
(setq bb (aref grdy (sum 2 i)))
(setf(aref grde (sum cc k))bb)
(setq cc(+ cc 1))
(format t " -> ~3,d" bb)
(setq aa bb nk (+ nk 1))
)
)
(if(= aa n)(setq h n))
)
)(loop4)
(format t "\nPATH TIME 0")
(defun loop5() ;critical path time
(do ((h 2 (1+ h)))((> h k))
(setq aa (aref grde (sum h k)))
(setq bb (-(aref grdy (sum 5 aa))1))
(setf (aref grde (sum h l))bb)
(format t " ~3,d" bb)
(if(= aa k)(setq h n))
)
)(loop5)
(tm)
(format t "\nPress enter to continue!")(read-line)
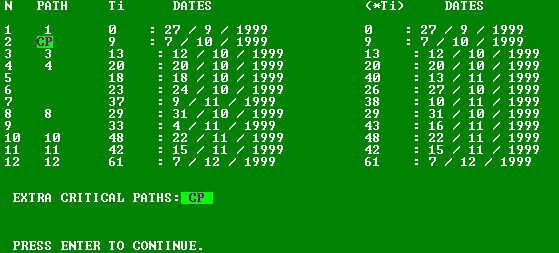
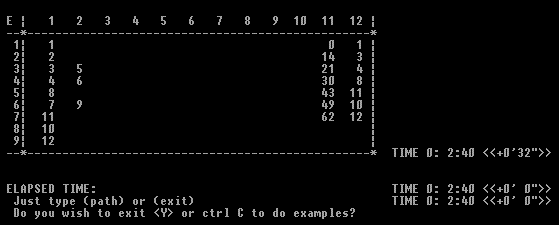
(do ((h 1 (1+ h)))((> h nk))
(do ((i 2 (1+ i)))((> i k))
(if (=(aref grde (sum h i))0)(setf (aref grde (sum h i))" "))
)
)
(setf (aref grde (sum 1 (- k 1)))0)
(scrn grde nk 'E)
(format t "\n\nELAPSED TIME: ")(tm)
)(path)
;********** WORD PERMUTATION ** STRING.LSP *******************************
(defun tst()
;;cagim m[a]g[i]c
;;senwy [n]ew[s]y
;;ramtry [m]ar[t]yr
;;rugbby [g][r]ubby
;;ai/ns/mt/gr
;;AINSMTGR;;40,320=2*3*4*5*6*7*8
;;; 20FEB2002 ;;; N.K.VAN VLIET ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
(unless (fboundp 'strcat)
(defun strcat (&rest str)
(apply #'concatenate 'string str)
)
)
(gc)
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
(defun rotatn(x y &optional (w "" s))
(setq d (if s (length w) 0))
;;(pr "ROTATN ")(princ x)(princ " ")(princ w)(princ " ")(princ y)(princ " d= ")(princ d)(princ " s= ")(princ s)
(if (>(- y 1)0)
(if (>= d 2) (progn
(setq a (subseq w 0 1) b (subseq w 1 ))
(rotatn x (- y 1) (strcat b a)); w rotated len times
)))
(if s (rotn x y w)(dsply x))
)
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
(defun rotn(x y &optional (w "" s))
(setq d (if s (length w) 0))
(if (and (>= d 1) s)
(progn (setq a (if (> d 0) (subseq w 0 1) ""))
(setq b (if (> d 1) (subseq w 1 2) ""))
(setq c (if (> d 1) (subseq w 1 ) ""))
(rotatn (strcat x a) (length c) c)
)(dsply x); print
))
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
(defun dsply(x) (setq nvv (+ 1 nvv))
(pr " => ")(princ x)(princ " ") (princ nvv) ;;
;;
(if (=(*(truncate nvv 12)12) nvv)(read-line));;every 12 lines
;;(do((i 0(1+ i)))((> i 9000)));; fast rotation
)
;(;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
(defun main(x)
(PR " WORD ")(princ x)
(setq nvv 0)
(rotatn "" (length x) x)
(pr "DONE!")
(pr "DONE!")
(read-line)
)(main "RAMTRY");;720;;(main "SENWY");;1209 ;;(main "AISEMTGR");;40,320
(o)
;;;;;;;;;;;;;;;;;;;;;;;;;;)
)(tst)
LOGIC MENU | HOME PAGE