Special Relativity Theory

Newton's laws of motion give us a complete description of the behavior moving objects at low speeds. The laws are different at speeds reached by the particles at SLAC.

Einstein's Special Theory of Relativity describes the motion of particles moving at close to the speed of light. In fact, it gives the correct laws of motion for any particle. This doesn't mean Newton was wrong, his equations are contained within the relativistic equations. Newton's "laws" provide a very good approximate form, valid when v is much less than c. For particles moving at slow speeds (very much less than the speed of light), the differences between Einstein's laws of motion and those derived by Newton are tiny. That's why relativity doesn't play a large role in everyday life. Einstein's theory supercedes Newton's, but Newton's theory provides a very good approximation for objects moving at everyday speeds.

Einstein's theory is now very well established as the correct description of motion of relativistic objects, that is those traveling at a significant fraction of the speed of light.

Because most of us have little experience with objects moving at speeds near the speed of light, Einstein's predictions may seem strange. However, many years of high energy physics experiments have thoroughly tested Einstein's theory and shown that it fits all results to date.

Theoretical Basis for Special Relativity

Einstein's theory of special relativity results from two statements -- the two basic postulates of special relativity:

The speed of light is the same for all observers, no matter what their relative speeds.
The laws of physics are the same in any inertial (that is, non-accelerated) frame of reference. This means that the laws of physics observed by a hypothetical observer traveling with a relativistic particle must be the same as those observed by an observer who is stationary in the laboratory.
Given these two statements, Einstein showed how definitions of momentum and energy must be refined and how quantities such as length and time must change from one observer to another in order to get consistent results for physical quantities such as particle half-life. To decide whether his postulates are a correct theory of nature, physicists test whether the predictions of Einstein's theory match observations. Indeed many such tests have been made -- and the answers Einstein gave are right every time!

The Speed of Light is the same for all observers.
The first postulate -- the speed of light will be seen to be the same relative to any observer, independent of the motion of the observer -- is the crucial idea that led Einstein to formulate his theory. It means we can define a quantity c, the speed of light, which is a fundamental constant of nature.

Note that this is quite different from the motion of ordinary, massive objects. If I am driving down the freeway at 50 miles per hour relative to the road, a car traveling in the same direction at 55 mph has a speed of only 5 mph relative to me, while a car coming in the opposite direction at 55 mph approaches me at a rate of 105 mph. Their speed relative to me depends on my motion as well as on theirs.

Physics is the same for all inertial observers.
This second postulate is really a basic though unspoken assumption in all of science -- the idea that we can formulate rules of nature which do not depend on our particular observing situation. This does not mean that things behave in the same way on the earth and in space, e.g. an observer at the surface of the earth is affected by the earth's gravity, but it does mean that the effect of a force on an object is the same independent of what causes the force and also of where the object is or what its speed is.

Einstein developed a theory of motion that could consistently contain both the same speed of light for any observer and the familiar addition of velocities described above for slow-moving objects. This is called the special theory of relativity, since it deals with the relative motions of objects.

Note that Einstein's General Theory of Relativity is a separate theory about a very different topic -- the effects of gravity.

Relativistic Definitions

Physicists call particles with v/c comparable to 1 "relativistic" particles. Particles with v/c << 1 (very much less than one) are "non-relativistic." At SLAC, we are almost always dealing with relativistic particles. Below we catalogue some essential differences between the relativistic quantities the more familiar non-relativistic or low-speed approximate definitions and behaviors.

Gamma (^y)
The measurable effects of relativity are based on gamma. Gamma depends only on the speed of a particle and is always larger than 1. By definition:

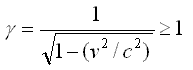
c is the speed of light
v is the speed of the object in question

For example, when an electron has traveled ten feet along the accelerator is has a speed of 0.99c, and the value of gamma at that speed is 7.09. When the electron reaches the end of the linac, its speed is 0.99999999995c where gamma equals 100,000.

What do these gamma values tell us about the relativistic effects detected at SLAC? Notice that when the speed of the object is very much less than the speed of light (v << c), gamma is approximately equal to 1. This is a non-relativistic situation (Newtonian).

Momentum
For non-relativistic objects Newton defined momentum, given the symbol p, as the product of mass and velocity -- p = m v. When speed becomes relativistic, we have to modify this definition -- p = gamma (mv)

Notice that this equation tells you that for any particle with a non-zero mass, the momentum gets larger and larger as the speed gets closer to the speed of light. Such a particle would have infinite momentum if it could reach the speed of light. Since it would take an infinite amount of force (or a finite force acting over an infinite amount of time) to accelerate a particle to infinite momentum, we are forced to conclude that a massive particle always travels at speeds less than the speed of light.

Some text books will introduce the definition m0 for the mass of an object at rest, calling this the "rest mass" and define the quantity (M = gamma m0) as the mass of the moving object. This makes Newton's definition of momentum still true provided you choose the correct mass. In particle physics, when we talk about mass we always mean mass of an object at rest and we write it as m and keep the factor of gamma explicit in the equations.

Energy
Probably the most famous scientific equation of all time, first derived by Einstein is the relationship E = mc2.

This tells us the energy corresponding to a mass m at rest. What this means is that when mass disappears, for example in a nuclear fission process, this amount of energy must appear in some other form. It also tells us the total energy of a particle of mass m sitting at rest.

Einstein also showed that the correct relativistic expression for the energy of a particle of mass m with momentum p is E2 = m2c4 + p2c2. This is a key equation for any real particle, giving the relationship between its energy (E), momentum ( p), and its rest mass (m).

If we substitute the equation for p into the equation for E above, with a little algebra, we get E = gamma mc2, so energy is gamma times rest energy. (Notice again that if we call the quantity M =gamma m the mass of the particle then E = Mc2 applies for any particle, but remember, particle physicists don't do that.)

Let's do a calculation. The rest energy of an electron is 0.511 MeV. As we saw earlier, when an electron has gone about 10 feet along the SLAC linac, it has a speed of 0.99c and a gamma of 7.09. Therefore, using the equation E = gamma x the rest energy, we can see that the electron's energy after ten feet of travel is 7.09 x 0.511 MeV = 3.62 MeV. At the end of the linac, where gamma = 100,000, the energy of the electron is 100,000 x 0.511 MeV = 51.1 GeV.

The energy E is the total energy of a freely moving particle. We can define it to be the rest energy plus kinetic energy (E = KE + mc2) which then defines a relativistic form for kinetic energy. Just as the equation for momentum has to be altered, so does the low-speed equation for kinetic energy (KE = (1/2)mv2). Let's make a guess based on what we saw for momentum and energy and say that relativistically KE = gamma(1/2)mv2. A good guess, perhaps, but it's wrong.

Now here is an exercise for the interested reader. Calculate the quantity KE = E - mc2 for the case of v very much smaller than c, and show that it is the usual expression for kinetic energy (1/2 mv2) plus corrections that are proportional to (v/c)2 and higher powers of (v/c). The complicated result of this exercise points out why it is not useful to separate the energy of a relativistic particle into a sum of two terms, so when particle physicists say "the energy of a moving particle" they mean the total energy, not the kinetic energy.

Another interesting fact about the expression that relates E and p above (E2 = m2c4 + p2c2), is that it is also true for the case where a particle has no mass (m=0). In this case, the particle always travels at a speed c, the speed of light. You can regard this equation as a definition of momentum for such a mass-less particle. Photons have kinetic energy and momentum, but no mass!

In fact Einstein's relationship tells us more, it says Energy and mass are interchangeable. Or, better said, rest mass is just one form of energy. For a compound object, the mass of the composite is not just the sum of the masses of the constituents but the sum of their energies, including kinetic, potential, and mass energy. The equation E=mc2 shows how to convert between energy units and mass units. Even a small mass corresponds to a significant amount of energy.

In the case of an atomic explosion, mass energy is released as kinetic energy of the resulting material, which has slightly less mass than the original material.
In any particle decay process, some of the initial mass energy becomes kinetic energy of the products.
Even in chemical processes there are tiny changes in mass which correspond to the energy released or absorbed in a process. When chemists talk about conservation of mass, they mean that the sum of the masses of the atoms involved does not change. However, the masses of molecules are slightly smaller than the sum of the masses of the atoms they contain (which is why molecules do not just fall apart into atoms). If we look at the actual molecular masses, we find tiny mass changes do occur in any chemical reaction.

At SLAC, and in any particle physics facility, we also see the reverse effect -- energy producing new matter. In the presence of charged particles a photon (which only has kinetic energy) can change into a massive particle and its matching massive antiparticle. The extra charged particle has to be there to absorb a little energy and more momentum, otherwise such a process could not conserve both energy and momentum. This process is one more confirmation of Einstein's special theory of relativity. It also is the process by which antimatter (for example the positrons accelerated at SLAC) is produced.

Units of Mass, Energy, and Momentum

Instead of using kilograms to measure mass, physicists use a unit of energy -- the electron volt. It is the energy gained by one electron when it moves through a potential difference of one volt. By definition, one electron volt (eV) is equivalent to 1.6 x 10-19 joules.

Lets look at an example of how this energy unit works. The rest mass of an electron is 9.11 x 10-31 kg. Using E = mc2 and a calculator we get:

E = 9.11 x 10-31 kg x (3 x 108 m/s)2 = 8.199 x 10-14 joules

This gives us the energy equivalent of one electron. So, whether we say we have 9.11 x 10-31 kg or 8.199 x 10-14 joules, we really talking about the same thing -- an electron. Physicists go one stage further and convert the joules to electron volts. This gives the mass of an electron as 0.511 MeV (about half a million eV).

So if you ask a high energy physicist what the mass of an electron is, you'll be told the answer in units of energy. You can blame Einstein for that!

Eagle-eyed readers will notice that if you solve E=mc2 for m, you get m=E/c2, so the unit of energy should be eV/c2. What happened to the c2? It's very simple, particle physicists choose units of length so that the speed of light = 1! How can we do that? Quite easily, as long as everyone understands the system. All we have to do is use a conversion factor to get back the "real" (i.e. everyday) units, if we want them.

Not only are mass and energy measured in eV, so is momentum. It makes life so much easier than dividing by c2 or c all the time.

There is more information available on units in relativistic physics.

Peculiar Relativistic Effects

Length Contraction and Time Dilation
One of the strangest parts of special relativity is the conclusion that two observers who are moving relative to one another, will get different measurements of the length of a particular object or the time that passes between two events.

Consider two observers, each in a space-ship laboratory containing clocks and meter sticks. The space ships are moving relative to each other at a speed close to the speed of light. Using Einstein's theory:

Each observer will see the meter stick of the other as shorter than their own, by the same factor gamma (- defined above). This is called length contraction.
Each observer will see the clocks in the other laboratory as ticking more slowly than the clocks in his/her own, by a factor gamma. This is called time dilation.
In particle accelerators, particles are moving very close to the speed of light where the length and time effects are large. This has allowed us to clearly verify that length contraction and time dilation do occur.

Time Dilation for Particles
Particle processes have an intrinsic clock that determines the half-life of a decay process. However, the rate at which the clock ticks in a moving frame, as observed by a static observer, is slower than the rate of a static clock. Therefore, the half-life of a moving particles appears, to the static observer, to be increased by the factor gamma.

For example, let's look at a particle sometimes created at SLAC known as a tau. In the frame of reference where the tau particle is at rest, its lifetime is known to be approximately 3.05 x 10-13 s. To calculate how far it travels before decaying, we could try to use the familiar equation distance equals speed times time. It travels so close to the speed of light that we can use c = 3x108 m/sec for the speed of the particle. (As we will see below, the speed of light in a vacuum is the highest speed attainable.) If you do the calculation you find the distance traveled should be 9.15 x 10-5 meters.

d = v t

d = (3 x 108 m/sec)( 3.05 x 10-13 s) = 9.15 x 10-5 m

Here comes the weird part - we measure the tau particle to travel further than this!

Pause to think about that for a moment. This result is totally contradictory to everyday experience. If you are not puzzled by it, either you already know all about relativity or you have not been reading carefully.

What is the resolution of this apparent paradox? The answer lies in time dilation. In our laboratory, the tau particle is moving. The decay time of the tau can be seen as a moving clock. According to relativity, moving clocks tick more slowly than static clocks.

We use this fact to multiply the time of travel in the taus moving frame by gamma, this gives the time that we will measure. Then this time times c, the approximate speed of the tau, will give us the distance we expect a high energy tau to travel.

What is gamma in this case? It depends on the tau's energy. A typical SLAC tau particle has a gamma = 20. Therefore, we detect the tau to decay in an average distance of 20 x (9.15 x 10-5 m) = 1.8 x 10-3 m or approximately 1.8 millimeters. This is 20 times further than we expect it to go if we use classical rather than relativistic physics. (Of course, we actually observe a spread of decay times according to the exponential decay law and a corresponding spread of distances. In fact, we use the measured distribution of distances to find the tau half-life.)

Observations particles with a variety of velocities have shown that time dilation is a real effect. In fact the only reason cosmic ray muons ever reach the surface of the earth before decaying is the time dilation effect.

Length Contraction
Instead of analyzing the motion of the tau from our frame of reference, we could ask what the tau would see in its reference frame. Its half-life in its reference frame is 3.05 x 10-13 s. This does not change. The tau goes nowhere in this frame.

How far would an observer, sitting in the tau rest frame, see an observer in our laboratory frame move while the tau lives?

We just calculated that the tau would travel 1.8 mm in our frame of reference. Surely we would expect the observer in the tau frame to see us move the same distance relative to the tau particle. Not so says the tau-frame observer -- you only moved 1.8 mm/gamma = 0.09 mm relative to me. This is length contraction.

How long did the tau particle live according to the observer in the tau frame? We can rearrange d = v x t to read t = d/v. Here we use the same speed, Because the speed of the observer in the lab relative to the tau is just equal to (but in the opposite direction) of the speed of the tau relative to the observer in the lab, so we can use the same speed. So time = 0.09 x 10-3 m/(3 x 108)m/sec = 3.0 x 10-13 sec. This is the half-life of the tau as seen in its rest frame, just as it should be!