Peg Solitaire
|
These pages were created and are maintained by
George Bell
(gibell@comcast.net)
Last Modified April 12th, 2009
Copyright © 2009 by George I. Bell
|
|
We can merely mention bean-bags, peg-boards,
size and form boards, as some apparatus found useful
for the purpose of amusing and instructing the weak-minded.
Albutt's "System of Medicine", 1899, VIII, 246 ([B3])
|
Table of Contents:
- Introduction
- Preliminaries
- Boards:
English,
6x6,
French,
Diamond41,
Diamond32,
Diamond13 (Hoppers),
Wiegleb,
9x9,
Antique English,
Rectangular,
Generalized Cross
- Online Games and Puzzles
- Solution Catalogs
- Computational Search Techniques
- How Hard Is Peg Solitaire?
- References
Introduction
Peg solitaire
is a classical puzzle commonly played on a 33-hole cross-shaped board
(also called "the English Board") or a
15-hole triangular board.
In England it is known as "Solitaire", but in the U.S. this refers
to a card game
so it is known as "Peg Solitaire".
Other people know it as "Hi-Q" because a popular version of the game sells
under that trade name.
In India it is known as "Brainvita".
This one-person game (or puzzle) first appeared in France
in the late 17th century.
|
The "Central Game"
|

|
A carefully
selected
sequence
of jumps
|

|
The starting
board position |
|
The target
board position |
|
The basic game consists of a cross-shaped board, usually made of wood,
together with a set of pegs, or more commonly marbles.
To start the game, one fills the board with pegs except for the central hole.
A jump consists of jumping one peg over another into an empty spot in
the board, removing the peg jumped over from the board.
Diagonal jumps are not allowed (in the standard version of the game).
The goal is to choose a sequence of jumps and finish with as few pegs as
possible, ideally a single peg in the center.
It seems almost everybody has run into this puzzle at some point.
Boards range from drilled planks using golf tees,
to beautifully crafted hardwood boards with indentations for marbles,
including a nice rim around the edge for storage of marbles as they are removed.
Computer versions of the game are also common
(see my Javascript games below).
After unsuccessful attempts at a "manual solution", many people
(myself included) try to write a simple computer program to solve it.
Even if there are only 4-8 jumps available at each board position,
this can lead to a prohibitively large number of possible jump
sequences after only 15 jumps.
This game is much older than the computer, and it is remarkable how
much was proved about this game without the aid of computers.
Instead of trying to memorize a computer solution, or a
YouTube video,
the best way to remember a solution is to
understand "block removals" or "packages",
sequences of moves that remove a whole block of pegs but leave
the rest of the board untouched.
Once you understand and have mastered the "3-removal", "6-removal"
and "L-move", the central game rapidly goes from frustrating to
being quite simple
(see [B1], [B3] or
[W2] for details).
This is similar to Rubik's cube in that you memorize a specific
sequence of moves that place you closer to your goal but do not mess
up the rest of the board.
After the central game above has been solved, what then?
We can try to define the "best possible" solution.
All solutions have exactly 31 jumps,
because we start with 32 pegs and one is lost with each jump.
However, when the same peg jumps one or more pegs,
we call this one move.
The question is, what is the solution with the least number of moves?
This question may be rephrased more informally as: what is the solution
that involves touching the smallest number of pegs?
This question turns out to be much harder to answer than simply finding a
solution to the central game.
The following terminology is useful in referring to moves involving multiple
jumps: when a peg removes n pegs in a single move, we refer to it
as a sweep, or more specifically, an n-sweep.
A sweep that begins and ends at the same board location
is called a loop.
This web site will not show you how to play peg solitaire.
It documents my own efforts to answer difficult or unsolved questions about
the game,
often involving boards different from than the standard board.
Most of the rest of this page concerns the search (by computer) for solutions
to certain problems with the least number of moves
(called minimal length solutions).
The boards on this page have holes based on a square lattice; each hole
has (at most) 4 neighbors.
It is also possible to play on a triangular lattice,
where each hole has (at most) 6 neighbors.
I now have a separate page for
Triangular Peg Solitaire.
If you want some tips and solutions for the 15-hole triangular board,
check out my page on
tips and solutions for the Cracker Barrel Puzzle.
Preliminaries
Board Notation and Identification
Because each board location is
generally marked by a depression or hole, in which the marble or
peg sits, we often refer to a board location as a hole.
We need some kind of notation to identify board locations.
On the cross-shaped 33-hole board the most common notation
is to label the board columns a-g (left to right) and the rows 1-7
(top to bottom).
This notation works well for any board that fits inside a 7x7 square,
and is referred to as "Standard 7x7 Notation".
An alternative notation where the holes are numbered consecutively is
not recommended because it must be changed every time the board shape changes.
|
|
 |
 |
 |
 |
 |
|
|
|
|
 |
c1 |
d1 |
e1 |
 |
|
|
 |
 |
 |
c2 |
d2 |
e2 |
 |
 |
 |
 |
a3 |
b3 |
c3 |
d3 |
e3 |
f3 |
g3 |
 |
 |
a4 |
b4 |
c4 |
d4 |
e4 |
f4 |
g4 |
 |
 |
a5 |
b5 |
c5 |
d5 |
e5 |
f5 |
g5 |
 |
 |
 |
 |
c6 |
d6 |
e6 |
 |
 |
 |
|
|
 |
c7 |
d7 |
e7 |
 |
|
|
|
|
 |
 |
 |
 |
 |
|
|
|
|
|
|
 |
 |
 |
 |
 |
|
|
| y= 3 |
|
|
 |
|
|
|
 |
|
|
| y= 2 |
 |
 |
 |
|
|
|
 |
 |
 |
| y= 1 |
 |
|
 |
|
 |
|
 |
|
 |
| y= 0 |
 |
|
|
 |
|
 |
|
|
 |
| y=-1 |
 |
|
|
 |
 |
 |
|
|
 |
| y=-2 |
 |
 |
 |
|
|
|
 |
 |
 |
| y=-3 |
|
|
 |
|
|
|
 |
|
|
|
|
|
 |
 |
 |
 |
 |
|
|
| x= |
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
Standard 7x7 Notation
[used by Beasley]
|
The bulky but general alternative:
Cartesian Coordinates
|
For larger boards, this coordinate system must be extended.
"Standard 9x9 Notation" is the obvious extension,
where the columns are a-i and the rows 1-9
(the most interesting boards have an odd width, and that is
why we go from 7x7 to 9x9).
An unfortunate aspect of this notational switch is that the central hole
goes from being called "d4" to "e5".
An alternative notation is Cartesian Coordinates, where the center
of the board is (0,0).
In standard 7x7 notation, to refer to a jump we simply list the
starting and ending board locations separated by a dash, i.e. "e5-e3"
for one of the jumps available above,
and "e5-e3-c3-a3" for the 3-sweep move "e5-e3, e3-c3, c3-a3".
Any hole on the board that cannot be jumped over is called a corner hole.
The standard board above has 8 corners: c1, e1, a3, g3, a5, g5, c7 and e7.
The number and geometry of the corners is an important aspect of any peg
solitaire board.
We will call a board gapless if for any two board locations
in the same row or column, all the intervening points are also on the board.
All of the boards on this page are gapless, and this concept is mainly useful
to exclude pathological boards with interior holes or gaps along the edge.
A board is called rectangular-symmetric if it is unchanged when reflected
about the x- or y-axes, and rotationally-symmetric if it is unchanged
by any 90 degree rotation.
A board is called square-symmetric if it is both rectangular-symmetric
and rotationally-symmetric.
Finally, a square-symmetric board with a unique central hole
is called odd because its width is odd, and it also
has an odd total number of holes.
We see that the board above is odd, square-symmetric and gapless.
Null-Class Boards
The general peg solitaire problem is to play from a full board with one
peg missing to a board position where only one peg remains.
These problems are called single vacancy to single survivor problems.
The special problem where the initial vacancy and survivor are the same board
location is called the (single vacancy) complement problem.
How do we know which single vacancy to single survivor problems are
potentially solvable?
This is answered very elegantly using parity arguments along the diagonals.
The arguments below have been "rediscovered" an amazing number of times.
The earliest known reference goes back to 1842.
Mathematicians enjoy using group theory to derive these results, however the
simple parity arguments below suffice.
Consider a diagonal labeling of the board holes (in two ways) as shown below:
|
|
 |
 |
 |
 |
 |
|
|
|
|
 |
1 |
2 |
3 |
 |
|
|
 |
 |
 |
2 |
3 |
1 |
 |
 |
 |
 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
 |
 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
 |
 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
 |
 |
 |
 |
3 |
1 |
2 |
 |
 |
 |
|
|
 |
1 |
2 |
3 |
 |
|
|
|
|
 |
 |
 |
 |
 |
|
|
|
|
|
 |
 |
 |
 |
 |
|
|
|
|
 |
4 |
5 |
6 |
 |
|
|
 |
 |
 |
6 |
4 |
5 |
 |
 |
 |
 |
6 |
4 |
5 |
6 |
4 |
5 |
6 |
 |
 |
5 |
6 |
4 |
5 |
6 |
4 |
5 |
 |
 |
4 |
5 |
6 |
4 |
5 |
6 |
4 |
 |
 |
 |
 |
5 |
6 |
4 |
 |
 |
 |
|
|
 |
4 |
5 |
6 |
 |
|
|
|
|
 |
 |
 |
 |
 |
|
|
|
Given a board position B,
let Ni(B) be the number of pegs in the cells marked i,
and T(B) be the total number of pegs on the board.
Now consider what happens to these functions after a solitaire jump is executed.
The total number of pegs T always goes down by one, while one of
N1, N2 or N3
increases by one while the other two decrease by one
(and similarly for N4, N5,
N6).
Therefore the evenness or oddness of the differences T-Ni
does not change as the game is played.
This partitions the set of all possible boards into
sixteen position classes depending on the parity (even or oddness)
of the six numbers:
(T-N1,T-N2,T-N3,T-
N4,T-N5,T-N6).
As you play solitaire you cannot leave the position class that you start in.
[You might think there should be 26 or 64 position classes.
However the numbers Ni are not independent, because
T = N1+N2+N3 =
N4+N5+N6,
and this implies that among (T-N1,T-
N2,T-N3),
there are either zero or two odd parities (and similarly for the other half)
and the number of position classes is reduced to 24 or 16].
At the standard starting position with only the center hole vacant,
you can easily check that
N1=N3=N4=N6
=11,
N2=N5=10,
and the total number of pegs T=32.
Therefore the 6 starting parities (T-Ni), i=1,2, ... 6
and therefore
the position class of the board is (Odd, Even, Odd, Odd, Even, Odd).
All board positions reachable from
this starting position must be in this same position class.
The position class of a board position with only a single peg is easy to
calculate,
it is odd on all diagonals except for the two the peg is in.
Hence we see that the only possible finishing locations for the game must
be the intersections between diagonals 2 and 5, or the board locations
(0,0)=d4, (3,0)=g4, (0,3)=d1, (-3,0)=a4 or (0,-3)=d7.
Consider the board position with every peg filled.
Then T=33, Ni=11 for all i, and all six
parities are Even.
The empty board with no pegs also lies
in the same position class: (Even,Even,Even,Even,Even,Even).
This is the defining property of a null-class board: any board position
and its complement are always in the same position class (the
complement
of a board position is the board position where each peg is replaced by a hole
and
vice versa).
It is important to realize that null-class boards are special, and not all
boards
are null-class boards.
By using the parity argument above, one can easily prove the following
two facts about null-class boards:
-
Only on a null-class board is it possible to solve the complement problem.
-
Consider a null-class board with an initial vacancy at
(x0,y0).
Then we can only finish with a single peg at
board positions (x1,y1) where the differences
x1-x0 and y1-y0 are multiples of 3.
Even on a null-class board, it is important to realize that the above
conditions do
not guarantee that a particular single vacancy to single survivor problem
can be solved (they are only necessary conditions).
What can we say if a board is not a null-class board?
We know that no complement problem is solvable, for starters.
Some single vacancy to single survivor problems may still be solvable,
but generally
only a few.
For details on all of this, see Beasley's book [B1].
From a practical standpoint, how do we determine whether a particular board
is null-class or not? The most obvious technique is to label the board in the
above fashion and count the number of 1's, 2's, 3's through 6's.
If these six numbers have the same parity (all odd or all even) then the board
is null-class, otherwise it is not.
A more clever technique is to apply local transformations to the full board
that do
not change the position class we are in, and try to reduce it to the empty
board.
A simple class of very useful transformations is to
take the complement of any three consecutive board locations
(vertically or horizontally).
A solitaire move itself is such a transformation, but there are others, such
as removing three pegs in a row,
or replacing two pegs separated by a hole by a peg in the hole.
Using this technique we can discover which position
class any pattern of pegs is in, and which finishing holes are possible.
Boards
The English "Standard" Board (33 holes)
 This board has been studied extensively, and is the only board many people
have played.
We just showed that this board is a null-class board.
A great deal can be proven about this board without the aid of a computer.
The book by John Beasley [B1]
is the authoritative reference and highly recommended.
A more general reference that is easy to obtain is
Winning Ways For Your Mathematical Plays [B3].
This four volume set was recently republished and Volume #4
contains the peg solitaire chapter, with a lot of info on this board.
This board has been studied extensively, and is the only board many people
have played.
We just showed that this board is a null-class board.
A great deal can be proven about this board without the aid of a computer.
The book by John Beasley [B1]
is the authoritative reference and highly recommended.
A more general reference that is easy to obtain is
Winning Ways For Your Mathematical Plays [B3].
This four volume set was recently republished and Volume #4
contains the peg solitaire chapter, with a lot of info on this board.
The English Board has more going for it than a pleasing shape.
It is the smallest
square-symmetric,
gapless board on which
the central game is solvable (see [P3]).
In fact, every
complement problem is solvable
on this board.
Ernest Bergholt found an 18-move solution to the central game in 1912, and
this was proven analytically to be minimal length by
John Beasley in 1964 [B1].
Since then the problem of finding minimal length solutions has been attacked by several
people using a computer, and minimal length solutions to all
single vacancy to single survivor problems have been found.
If diagonal jumps are allowed, what is the shortest solution to the central game?
This problem was unresolved until recently.
Using a computer, it is not so easy to find the minimal length solution because
the number of moves from each board position is approximately double.
However I finally have been able to complete the calculation, to show that
the minimal length solution has 15 moves [P4].
 A web page on the shortest solution when
diagonal jumps are allowed.
A web page on the shortest solution when
diagonal jumps are allowed.
 A page with example computer calculations by
level for the English 33-hole board.
A page with example computer calculations by
level for the English 33-hole board.
The 6x6 Board (36 holes)
 This 36-hole board is the smallest square board on which a
complement problem is solvable.
It is the second smallest
square-symmetric, gapless board on which every
complement problem is solvable
(see [P3]).
In general it is less interesting than the English board, because
it lacks a central hole and has a simpler geometry.
It does, however, support some remarkably short solutions.
John W. Harris and Harry O. Davis studied this board in the 1960's,
and found that most single vacancy to single survivor
problems
can be solved in 15 moves, with a few cases requiring 16 moves.
This 36-hole board is the smallest square board on which a
complement problem is solvable.
It is the second smallest
square-symmetric, gapless board on which every
complement problem is solvable
(see [P3]).
In general it is less interesting than the English board, because
it lacks a central hole and has a simpler geometry.
It does, however, support some remarkably short solutions.
John W. Harris and Harry O. Davis studied this board in the 1960's,
and found that most single vacancy to single survivor
problems
can be solved in 15 moves, with a few cases requiring 16 moves.
This board does have one unusual property: it is possible for any peg on the
board
to reach some corner.
No matter where the final peg is to be left, it is possible
to arrange things so that the last four moves start from the four corners.
If this board is easy for you try finding solutions with this property.
You can see several of these corner finish solutions in the solution catalog.
It is not always possible to have a minimal length solution with this
corner finish property.
The French Board (37 holes)
 This board appears on the earliest known
printed reference to peg solitaire, an engraving dated 1697.
This board is not a null-class board, therefore no
complement problem is solvable on it.
There are ten single vacancy to single survivor problems
solvable on this board, and
each can be solved in 20 or 21 moves.
This board appears on the earliest known
printed reference to peg solitaire, an engraving dated 1697.
This board is not a null-class board, therefore no
complement problem is solvable on it.
There are ten single vacancy to single survivor problems
solvable on this board, and
each can be solved in 20 or 21 moves.
In Winning Ways For Your Mathematical Plays [B3]
this board is referred to as "the Continental Board".
Unfortunately, there is no standard name by which these boards are known.
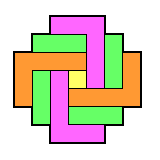 If you are solving a problem by hand, the best technique to use
(on any board) is to decompose it into block removals.
Note that the French board decomposes nicely into L and 3-removals
as shown in the figure on the right.
In order to solve a particular problem, one can modify this diagram
with appropriate starting and ending moves, as shown in the figures on the left.
If you are solving a problem by hand, the best technique to use
(on any board) is to decompose it into block removals.
Note that the French board decomposes nicely into L and 3-removals
as shown in the figure on the right.
In order to solve a particular problem, one can modify this diagram
with appropriate starting and ending moves, as shown in the figures on the left.
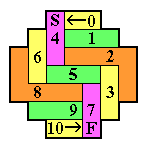
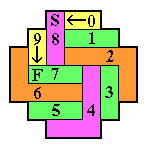
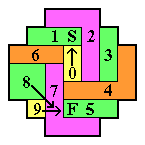 In each diagram, the location of the starting hole is marked by an "S",
and the finishing hole by an "F".
After dividing the board up into block removals,
one must also check that the catalyst needed by each block removal
is present.
The sequencing of the block removals is indicated by the numbering.
If you don't understand how to turn such a diagram into a solution,
read the introduction to block removals at [W2].
In each diagram, the location of the starting hole is marked by an "S",
and the finishing hole by an "F".
After dividing the board up into block removals,
one must also check that the catalyst needed by each block removal
is present.
The sequencing of the block removals is indicated by the numbering.
If you don't understand how to turn such a diagram into a solution,
read the introduction to block removals at [W2].
If the game begins with the center peg missing, this board position
is in the position class of the empty board, so it is not possible to
finish with one peg.
An elegant modification of the rules which allows for a d4 to d4 solution
is known as Cremers' Key
[W16].
According to [W16],
this trick was invented by Frans Cremers,
a retired teacher from Aalter, Belgium.
Play proceeds from the center as normally,
but the player is allowed to replace the
central peg once when the hole is unoccupied.
This puts the board position in the correct
position class,
and a solution can be obtained.
Click here
to see a center to center solution using Cremers' Key in 20 moves
(the shortest possible).
Note that Cremers' key works not only from the center start, but from
ANY start!
In the general case one is allowed to replace the peg at the starting
hole once.
The goal is to finish with one peg,
NOT at the starting location, but ALWAYS in the center.
The results of [P3] show
that Cremers' Key will put the board in the
position class
of the center finish on any gapless,
odd,
square-symmetric
board that is not null-class.
Another way to make the central game solvable is to allow diagonal jumps.
In this case the central game can be solved in as little as 13 moves.
Another interesting puzzle is to begin with pegs
at all locations except for the central 9 holes
{c3, c4, c5, d3, d4, d5, e3, e4, e5}, and try to
play to the complement of this position
with only the center 9 holes occupied.
Allowing diagonal jumps, this "big central game" is solvable, but
the same problem is not solvable on the 33-hole
English board.
The shortest possible solution to the "big central game" has 13 moves,
just like the normal central game.
 A web page on the shortest solution when diagonal jumps are allowed
A web page on the shortest solution when diagonal jumps are allowed
The 41-Hole Diamond Board
 This board is also known as "the Continental Board".
This is not a null-class board, and there are only
four single vacancy to single survivor problems
solvable on it (as shown in [B1]).
This board is very difficult to play on because it has 16
corners,
but this is really a significant constraint on play.
All four single vacancy to single survivor problems on this board
can be solved in 26 moves, but no fewer.
Look here
to view some solutions.
This board is also known as "the Continental Board".
This is not a null-class board, and there are only
four single vacancy to single survivor problems
solvable on it (as shown in [B1]).
This board is very difficult to play on because it has 16
corners,
but this is really a significant constraint on play.
All four single vacancy to single survivor problems on this board
can be solved in 26 moves, but no fewer.
Look here
to view some solutions.
This board is not easy to decompose into block removals.
In his book, Beasley
[B1] shows how to accomplish the task using more
complex block removals to deal with the corners.
One can try to obtain a center to center solution using the
Cremers' Key [W16]
rule modification, but it fails on this board.
Replacing the center peg does give one a board position in the
correct position class,
but using the resource count
shown below you can easily prove that it is not possible to finish
with one peg.
This board is a member of a general class known as a draughtsboard.
Such boards are obtained by taking any square board, and labeling the
holes alternately as on a chess or checkers board. Then the board is
rotated 45 degrees and the black squares define the holes of the draughtsboard.
The 41-hole diamond board can be so obtained starting from a 9x9 square board.
The 32-Hole Diamond Board

 This board is null-class but is not
square-symmetric
(only rectangular-symmetric).
It is a draughtsboard created from an 8x8 square
board,
and a convenient way to play this board is using a checkers board,
playing only on the squares of one color with diagonal jumps.
In fact this board is identical to a standard checkers board,
just rotated 45 degrees, as the figure on the right shows.
This board is null-class but is not
square-symmetric
(only rectangular-symmetric).
It is a draughtsboard created from an 8x8 square
board,
and a convenient way to play this board is using a checkers board,
playing only on the squares of one color with diagonal jumps.
In fact this board is identical to a standard checkers board,
just rotated 45 degrees, as the figure on the right shows.
This board has a similar size as the
standard English board, but it has 14
corners rather than 8.
In 1941, B. M. Stewart showed that all 25
single vacancy to single survivor problems
were solvable on this board.
My program has found that all of them are solvable in 17-19 moves,
with only the d1 (top hole) complement requiring 19 moves.
The central game can be solved in 18 moves, but no fewer.
The 13-Hole Diamond Board ("Hoppers" board)

 Hoppers is a peg solitaire game invented by Nob Yoshigahara and marketed by
ThinkFun.
If you rotate this board 45 degrees, it is easy to see that it
is a 13 hole Diamond Board, or
draughtsboard created from a 5x5 square board,
with the addition of diagonal jumps along both diagonals.
Without the addition of diagonal jumps, no
single vacancy to single survivor problem
on this board is solvable.
However with the diagonal jumps many problems become solvable,
and its small size makes solutions easier to work out.
An interesting advanced problem is to try to solve the
central game on this board in as few as 7 moves.
Hoppers is a peg solitaire game invented by Nob Yoshigahara and marketed by
ThinkFun.
If you rotate this board 45 degrees, it is easy to see that it
is a 13 hole Diamond Board, or
draughtsboard created from a 5x5 square board,
with the addition of diagonal jumps along both diagonals.
Without the addition of diagonal jumps, no
single vacancy to single survivor problem
on this board is solvable.
However with the diagonal jumps many problems become solvable,
and its small size makes solutions easier to work out.
An interesting advanced problem is to try to solve the
central game on this board in as few as 7 moves.
In 2007, ThinkFun
repackaged this game under the name "Cool Moves" with a completely
new card set.
 A web page with strategy tips for this board.
A web page with strategy tips for this board.
Wiegleb's Board (45 holes)
 This is one of the first boards to appear in print, in 1779 by J. C. Wiegleb.
It has since been almost totally ignored. It is a null-class board, and
also a
Generalized Cross Board (see below).
There are 36 different single vacancy to single survivor
problems on it,
all of which are solvable except for the (4,0) or e1
complement problem.
This is one of the first boards to appear in print, in 1779 by J. C. Wiegleb.
It has since been almost totally ignored. It is a null-class board, and
also a
Generalized Cross Board (see below).
There are 36 different single vacancy to single survivor
problems on it,
all of which are solvable except for the (4,0) or e1
complement problem.
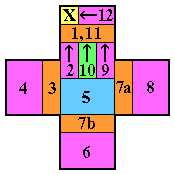
 The proof of the impossibility of the (4,0) or e1 complement is not a
simple matter, a brief outline of a proof is given in Beasley's book
[B1].
I have found an alternate proof by integer programming
techniques, but no short, simple proof has been found.
A computer proof by exhaustive search is possible,
but time consuming.
It feels like you are smashing a peanut with a sledgehammer.
This problem is several orders of magnitude harder than any
problem on the English Board.
The proof of the impossibility of the (4,0) or e1 complement is not a
simple matter, a brief outline of a proof is given in Beasley's book
[B1].
I have found an alternate proof by integer programming
techniques, but no short, simple proof has been found.
A computer proof by exhaustive search is possible,
but time consuming.
It feels like you are smashing a peanut with a sledgehammer.
This problem is several orders of magnitude harder than any
problem on the English Board.
Problems on this board can be solved most easily using block removals
as shown on the figures to the right.
The numbering shows the ordering of the block removals.
Numbers subdivided a, b, c are block removals that must be interleaved,
in other words part b begins before part a is finished.
To see the sequence of moves to solve the central game this way
see the solution given in
[W3].
Beasley [B1] gives block removal diagrams for
one other complement problem on this board.
The longest sweep that can appear in any solution to a
single vacancy to single survivor problem
has length 16, one such sweep is shown on the board above left.
There are three problems on this board for which a 16-sweep can occur,
these make for interesting problems to solve by hand:
- Vacate g4 (or equivalently d7), play to finish at d4 with
the last move a 16-sweep (the above board shows the last move).
- Vacate g5, play to finish at d2 with the last move a 16-sweep.
- Vacate g6, play to finish at d3 with the second to the last move a 16-sweep.
The 16-sweep begins and ends at d2.
You can go nuts trying to solve these playing forward.
The trick, of course, is to play backwards from the complement of the
position before the long sweep.
No other combination of starting and finishing holes can contain a 16-sweep,
except of course rotations or reflections of the above three problems.
The three problems above can be solved in a minimum of
22, 24, and 23 total moves, respectively.
For solutions, see [P2] or
this web page.
The solution catalog shows the shortest length solution to all
35 solvable problems on this board, an effort which took about
3 months of CPU time on a 1 GHz Pentium PC.
All of them are solvable in 20-23 moves,
with only the (3,0) or e2 complement requiring 23 moves.
There are a few problems on this board
with unique minimal length solutions,
at least up to symmetry and move order.
The central game can be solved in 22 moves, but no fewer.
 A web page of computational results for this board
A web page of computational results for this board
The 9x9 Board (81 holes)
 At first glance this null-class board doesn't seem very interesting.
You've seen one square board, you've seen them all, why not just quit at the
6x6?
However, unlike the 6x6, this square board does have a central hole,
which leads to more complexity in its solutions.
While all single vacancy to single survivor problems
are easy to solve using block removal methods,
this board supports some remarkably long sweeps.
A sweep of 34 is the longest geometrically possible,
shown on the board to the left.
What is more remarkable is that this particular sweep can be
reached from a single vacancy start.
At first glance this null-class board doesn't seem very interesting.
You've seen one square board, you've seen them all, why not just quit at the
6x6?
However, unlike the 6x6, this square board does have a central hole,
which leads to more complexity in its solutions.
While all single vacancy to single survivor problems
are easy to solve using block removal methods,
this board supports some remarkably long sweeps.
A sweep of 34 is the longest geometrically possible,
shown on the board to the left.
What is more remarkable is that this particular sweep can be
reached from a single vacancy start.
This board also represents a significant computational barrier.
On the standard 33-hole board, it is possible to answer any question
using a computer in a reasonable amount of time.
On that board, the total number of distinct board positions is
233, about 8.6 billion.
However only 1/16'th of these board positions lie in the same
position class
as the starting position, so the number of board positions reachable
from any single vacancy start is at most 229, about 540
million.
From an initial vacancy at c3 [or (1,1)] one can calculate that 264 million
board positions are reachable (and somewhat less from any other starting
location).
If we use 33 bits per board, storing all 264 million
board positions requires about 1 Gigabyte of hard drive space,
not that large a number by today's standards.
On the 9x9 board the total number of distinct board positions
is 281, which is greater than 1024.
Even if we assume 1/32 of them are reachable from a single vacancy start,
this is still 7x1022 board positions, which would require
7x1014 gigabytes of storage (assuming 81 bits per board).
By using symmetry and other ideas (for example we probably don't need
to compute all positions reachable anyway) we may be able to reduce this
by 2-4 orders of magnitude, reducing our storage requirements to a mere
hundred billion gigabytes!
These numbers give a good idea how much harder this board is
to deal with computationally compared to the standard 33-hole board.
 A web page on the 9x9 board.
A web page on the 9x9 board.

The Antique English Board (67 holes)
This board appeared in England around 1880.
It seems an attempt to create a larger version of the popular
33-hole cross-shaped board.
In [P3], we prove that there is only one board with
the following properties (1) square-symmetric,
(2) gapless,
(3) every complement problem is solvable,
(4) odd,
and (5) less than 81 holes.
The only board with all five of these properties is the
33-hole cross-shaped board.
For some reason two additional holes have also been added to the top
row of this board (breaking the square symmetry, as well as no longer being gapless).
The holes outlined in green appear to have some special significance--
it may have been that some special set of rules applied to this board.
Robert Reid has emailed me that this board is in David Parlett's
Oxford History of Board Games (p. 192),
and that the markings are for
a Fox and Geese
variant called "Siege".
He doubts this board was ever used to play peg solitaire.
It is not hard to show that this board shares the same problems as the
37-hole French board.
Namely, if one begins with a full board with only the center peg missing,
it is impossible to play to one peg.
This is true for the 67-hole board as well as the square-symmetric
65-hole version where the two holes on the ends of the top row
are removed.
Rectangular Boards
A rectangular board is null-class if and only if one of
the sides is a multiple of 3, or equivalently if the total number
of holes is a multiple of 3.
The smallest rectangular board where every
complement problem
is solvable is the 6x4 board.
Generalized Cross Boards
The 33-hole board can be thought of as a 3x3 "core" attached to
four 2x3 "arms".
One can generalize this concept by starting with the core
and adding four arms of size ni x 3,
creating an infinite set of peg solitaire boards with unequal
or even zero arm lengths.
Because they are built up from rows of three, these are all
null-class boards; however in general they lack symmetry.
I looked into these boards and discovered there are exactly
12 generalized cross boards where the
complement problem
is solvable at every board location.
Of these 12, the only board with square symmetry is the
standard 33-hole board.
Two are rectangular-symmetric
(top row of figure to the left),
three have rectangular symmetry about only one axis,
two have diagonal symmetry (second row) and the remaining
four have no symmetries at all
[W1].
 A web page on Generalized Cross Boards
(not available online).
A web page on Generalized Cross Boards
(not available online).
Triangular Boards
All the boards above are based on a square lattice.
One can also play peg solitaire on a triangular lattice.
As noted in Beasley [B1], solitaire on such a lattice
is equivalent to solitaire on a square lattice with the addition of
moves along one diagonal but not the other.
 There is now a separate web page for Triangular
Solitaire.
There is now a separate web page for Triangular
Solitaire.
Online Puzzles
It is not easy to find an actual game board of any shape other than the English,
French or 15-hole Triangular boards.
But it's easy to create any board on a computer.
This also has the added advantage of being able to include demos and
the ability to take back moves.
Here is a list of the games on this site.
These are all written in JavaScript, and you must have JavaScript
activated in your browser to view them.
Works best with Internet Explorer.
Solution Catalogs
Here is a complete listing of shortest length solutions for the boards above.
These were calculated by exhaustive computer search.
If you want to know how this was done, see the
Programming Ideas
section that follows this.
Given a board and a (solvable)
single vacancy to single survivor problem, there is
a minimum number of moves that can solve it.
These solutions have an elegant look to them and they tend to be extremely hard
to find by hand.
The table below shows a list of boards, together with some statistics about
each.
If you click on a board, you will see another table listing all single vacancy
to single survivor problems solvable on that board, together with information
about
these solutions.
These boards are all square-symmetric, and we only list unique
single vacancy to single survivor problems. In other words, if one problem
can be obtained from another by rotation and/or reflection, only one will be
listed.
If you keep clicking on the tables, you can view
diagrams of minimal length solutions.
The solution catalog shown may be incomplete.
Only those with a check mark before them can display all solutions.
It is labor intensive producing these and they may not be complete for some
time.
Some column heads you will see that require explanation:
- Number of Problems: This is the number of different solvable single
vacancy
to single survivor problems on this board (not including problems equivalent
by symmetry).
- Longest Sweep: The first column is the longest sweep possible in any
single vacancy to single survivor problem, regardless of solution length.
The second "Longest Sweep" column is the longest sweep possible in a
minimal length solution.
- Solution Lengths: This is the range in the number of moves in
the minimal length solutions, over all problems.
- Time to Calculate: This is the amount of CPU time that
was needed to calculate the underlying table (find all minimal
solutions to all problems).
| Board Name [click to see
catalog] |
Number
of Holes |
Null-Class?
|
Number of Problems |
Longest Sweep (any problem) |
Minimal Length Solution Properties |
| Solution Lengths |
Longest Sweep |
Time to Calculate |
 Diamond32
Diamond32
|
32 |
Yes |
35 |
8 or 9 |
17-19 |
8 |
2 hours |
 English
English
|
33 |
Yes |
21 |
9
† |
15-19 |
8 |
2 hours |
 6x6
6x6
|
36 |
Yes |
21 |
10 ‡ |
15-16 |
10 |
6 hours |
 French
French
|
37 |
No |
10 |
9 † |
20-21 |
9 |
24 hours |
 Diamond41
Diamond41
|
41 |
No |
4 |
9 |
26 |
9 |
3 hours |
 Wiegleb's
Wiegleb's
|
45 |
Yes |
35 |
16
‡ |
20-23 |
14 |
3 months |
|
Table Footnotes: (†) From John Beasley's book [B1].
(‡) This is the longest sweep geometrically possible on this board,
and at least one such sweep can be realized as the final move to a
single vacancy to single survivor problem.
|
The information in the above table has been calculated by other authors
in the case of the English, French and 6x6 boards.
My results have been checked against their results.
To my knowledge, nobody before has calculated minimal length solutions
for the 41-hole diamond and 45-hole Wiegleb's board.
Computational Search Techniques
 There are a number of techniques and programming tricks that can speed up
the search for minimum length solutions.
Many of these are primarily computer science concepts,
and I will mention only those ideas specific to peg solitaire.
There are a number of techniques and programming tricks that can speed up
the search for minimum length solutions.
Many of these are primarily computer science concepts,
and I will mention only those ideas specific to peg solitaire.
A good introductory reference which has a nice progression of problems is
the recent book by Koetke [B4].
This book starts out with small boards that are easy to solve,
and discusses the problems encountered as larger boards are considered.
It also has example programs in java.
This is one of the few peg solitaire references that contains a lot
of detail about solving the game computationally.
If you try to solve a peg solitaire problem in in inefficient manner your
program can take forever to run, even on the standard 33-hole board.
For example the most obvious technique is to store the sequence of moves
(or jumps) and try to exhaustively go through all possible sequences.
Because there are a large number of move sequences that result
in the same board position, such an algorithm is extremely inefficient.
One solution is to use a hash table or some other means to store board positions
seen previously so you do not have to investigate them farther.
A similar technique is to only keep track of the set of boards at
each level in the tree, rather than the moves.
I call this a search by levels.
This is much faster than a straight search over move sequences and can
solve any problem on the 33-hole board relatively quickly.
For boards larger than this, additional techniques are needed.
I have used four ideas to speed up a search by levels:
-
If the problem is symmetric, there is no need to search over solutions
that are really the same.
On the 33-hole English board this can help a lot for some problems
(for example the central game or d4 complement) but not on others
(for example the c1 complement).
- The use of resource counts or Pagoda functions as explained below (see
also [B1] or [B3]).
Whether this is useful computationally depends on the board as well as the
problem.
It is most helpful on the 41-hole Diamond Board.
- Search forward from the starting position and also backwards
from the desired final position, looking for matching board
positions in the middle.
This is known as a
bidirectional search.
A trade-off is that the programming is more complex.
-
A* search.
This works particularly well when
diagonal jumps are allowed.
For details see [P4].
Finally, one should be careful not to confuse the computer's
failure to find a solution with a proof that no solution exists.
These calculations are complex and lengthy,
particularly when resource counts, symmetry and forward/backward
calculations are all being used.
Logical bugs in the code can easily prevent the computer
from finding a solution, and much testing is required to make
sure the results are reasonable.
For example, no program that reports "no 17 move solution to the
English board central game" should be trusted unless it can find the
Bergholt solution in 18 moves.
You can also test your program by reproducing
these tables.
For more details on computational search techniques, see my paper
[P4].
Resource Counts
A resource count (sometimes called a Pagoda function) is a real valued
function on board states that cannot increase during play.
At first it may not be obvious that such functions exist, certainly only
very carefully chosen functions have this property.
The simplest (but least useful) example of a resource count has a value of +1
at all board locations. This function counts the number of pegs on the board
and decreases by one with every jump.
The most useful resource counts generally have negative values in
corners
(in fact, it is not hard to show that a resource count can only have
a negative value at a corner).
If a certain move leaves the board with a value that is less
than that of our final position, we know that this move cannot possibly lead
to a solution.
A very useful resource count on the 41-hole diamond board is:
|
|
|
|
 |
 |
 |
|
|
|
|
|
|
|
 |
 |
-1 |
 |
 |
|
|
|
|
|
 |
 |
-1 |
1 |
-1 |
 |
 |
|
|
|
 |
 |
-1 |
1 |
0 |
1 |
-1 |
 |
 |
|
 |
 |
-1 |
1 |
0 |
1 |
0 |
1 |
-1 |
 |
 |
 |
-1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
-1 |
 |
 |
 |
-1 |
1 |
0 |
1 |
0 |
1 |
-1 |
 |
 |
|
 |
 |
-1 |
1 |
0 |
1 |
-1 |
 |
 |
|
|
|
 |
 |
-1 |
1 |
-1 |
 |
 |
|
|
|
|
|
 |
 |
-1 |
 |
 |
|
|
|
|
|
|
|
 |
 |
 |
|
|
|
|
This resource count provides a constraint on board positions that
can appear in any single vacancy to single survivor problem.
One can show that for any single vacancy to single survivor problem on this
board,
after the first move and before the last move,
this resource count must always evaluate to zero.
This is a powerful constraint on the jumps available from
any board position (that can lead to a solution).
No solution can contain a jump over a peg in a hole marked "1"
(white squares) unless that jump starts at the edge of the board.
This constraint can be added to a computer program, and with it
this board is not much harder to find minimal solutions
(on a computer) than the 33-hole English board.
The above resource constraint can be applied
on the French board (by ignoring any value that is not on that board)
and it is still somewhat useful.
It can also be used on the English board,
but with only a very minor speed increase.
On Wiegleb's board a moderately useful resource count (for computations)
has a "-1" at the eight corners and "+1" at the
12 interior locations:
d2, f2, b4, d4, f4, h4, b6, d6, f6, h6, d8 and f8 (and zeros everywhere else).
How Hard Is Peg Solitaire?
 Most people will agree that solving the central game
on the standard 33-hole board is challenging.
In fact I once spent a weekend on this problem without success.
However I claim this just indicates approaching the problem by trial and error
(or exhaustive search) is very inefficient.
After you learn block removals (see [W2]),
the problem actually becomes quite simple.
It also seems that on any "well behaved" board, no matter how large, the
complement problem
should be relatively easy to solve using block removal methods.
An example of a well behaved board is any square board, but I believe
many other boards also fall into this category.
Most people will agree that solving the central game
on the standard 33-hole board is challenging.
In fact I once spent a weekend on this problem without success.
However I claim this just indicates approaching the problem by trial and error
(or exhaustive search) is very inefficient.
After you learn block removals (see [W2]),
the problem actually becomes quite simple.
It also seems that on any "well behaved" board, no matter how large, the
complement problem
should be relatively easy to solve using block removal methods.
An example of a well behaved board is any square board, but I believe
many other boards also fall into this category.
Consider a rather arbitrary board without any interior holes
(gapless).
This board might be quite large, and in the simplest case could be square.
We will try to quantify the difficulty of three different problems:
- Given an arbitrary pattern of pegs, determine if it
can be reduced to a single peg. In this case the specific shape of the board
is not important, we could even consider the board to be infinite.
- Given a complement problem on this board,
find any solution to it.
Here the shape of the board is very important.
The central game on the 33-hole board is an example of such a problem.
- Given a complement problem on this board,
find the shortest solution to it (minimum number of moves).
It was shown in 1990 [P1] that problem #1 is NP
Complete.
In practical terms this means that any algorithm to solve this problem will
have a run
time that increases exponentially with the problem size.
Like problem #1, problem #2 also asks if you can
reduce a pattern of pegs to a single peg.
Does this mean problem #2 is NP Complete also?
No it does not, because a complement problem does not
start from an arbitrary pattern of pegs.
The starting position has every hole occupied, except for the
starting vacancy, hence it is a very regular pattern.
Of course the shape of the board could still be somewhat complicated,
but as a gapless board it is only the edge that may be complicated.
It is still unknown how hard problem #2 is to solve.
Clearly if the board is not null-class,
there is no solution to problem #2 or #3 (we can also check in problem #1
if the configuration of pegs is in the position class of one peg or not).
It is very easy to check if a board is null-class, so we don't need to require
this.
As the difficult case we may as well assume all boards from now on
are null-class.
Suppose we consider problem #2 on an arbitrary
rectangular
null-class board (with both edges at least 4).
Finding a solution to a complement problem on such a board, I claim,
is actually very easy, and can probably be solved in linear time.
Why? Because this problem is easy to solve by hand using block removals.
You simply visually identify blocks of pegs
you need to remove and make sure the required catalyst is present and that
after the
block removal you don't strand any pegs too far away from the core bunch.
You also need to be careful near the edge of the board.
This logic could be programmed, and would result in a computer algorithm
that could solve complement problems on rectangular boards
extremely quickly.
Even boards which are "not too different" from a rectangular board should also
be easy.
It is rather difficult to quantify "not too different", but basically any
gapless
null-class board that doesn't have any tight spaces can be solved using block
removals.
The standard 33-hole board should fit into this category.
It easier to complete this argument on
triangular boards,
and I now have a
simple algorithm
that can solve any single vacancy problem on a triangular board
of arbitrary size.
In summary, problem #1 has been proven NP Complete.
I believe problem #2 is not very hard on "well behaved" boards,
which include at least rectangular boards (and certainly triangular boards).
Problem #3 is very difficult on
any board with more than about 50 holes, and I believe no algorithm can find
shortest solutions in polynomial time.
Peg Solitaire References
See also
triangular peg solitaire references.
Books
| B1. | |
John D. Beasley,
The Ins & Outs of Peg Solitaire,
Oxford Univ. Press, 1985
(the paperback Edition 1992, contains an additional page: Recent Developments)
ISBN 0-19-286145-X (paperback).
|
| B2. | |
Martin Gardner,
The Unexpected Hanging and Other Mathematical Diversions,
University Of Chicago Press, 1991 (paperback), pp. 122-135
ISBN 0-22-628256-2.
[The chapter "Peg Solitaire" is based on a
Scientific American column that appeared in the June, 1962 edition.]
|
| B3. | |
John H. Conway, Elwyn R. Berlekamp, Richard K. Guy,
Winning Ways for Your Mathematical Plays, Volume 4,
AK Peters, 2004
(second edition).
|
| B4. | |
Walter Koetke,
Classic Thinking Games with Java,
Basics & Beyond, Inc., 2007.
|
| B5. | |
George I. Bell, Peg Solitaire with Diagonal Jumps, in
Ed Pegg Jr., Alan H. Schoen, Tom Rodgers (Editors)
Mathematical Wizardry for a Gardner,
AK Peters, 2009.
|
Papers
| P1. | |
Ryuhei Uehara and Shigeki Iwata,
Generalized Hi-Q is NP-complete,
Trans. IEICE, E73, pp.270-273, 1990
|
| P2. | |
George I. Bell and John D. Beasley,
New Problems on Old Solitaire Boards,
Board Game Studies #8,
presented for the 8th international colloquium on board game studies,
Oxford, England in April 2005.
|
| P3. | |
George I. Bell,
A Fresh Look at Peg Solitaire,
Mathematics Magazine, 80:16-28, 2007.
|
| P4. | |
George I. Bell,
Diagonal Peg Solitaire,
INTEGERS Electronic Journal of Combinatorial Number Theory,
Vol 7, G1, 2007.
|
| P5. | |
G. DuPuy, D. Taylor,
Using Board Puzzles to Teach Operations Research,
INFORMS Transactions on Education,
Volume 7, Number 2, January 2007.
|
| P6. | |
George I. Bell,
Notes on solving and playing peg solitaire on a computer, 2009.
|
Web References
Copyright © 2009 by George I. Bell
 To triangular lattice peg solitaire
To triangular lattice peg solitaire
 To the peg solitaire army
To the peg solitaire army
 To my home page
To my home page




 This 36-hole board is the smallest square board on which a
complement problem is solvable.
It is the second smallest
square-symmetric, gapless board on which every
complement problem is solvable
(see [P3]).
In general it is less interesting than the English board, because
it lacks a central hole and has a simpler geometry.
It does, however, support some remarkably short solutions.
John W. Harris and Harry O. Davis studied this board in the 1960's,
and found that most single vacancy to single survivor
problems
can be solved in 15 moves, with a few cases requiring 16 moves.
This 36-hole board is the smallest square board on which a
complement problem is solvable.
It is the second smallest
square-symmetric, gapless board on which every
complement problem is solvable
(see [P3]).
In general it is less interesting than the English board, because
it lacks a central hole and has a simpler geometry.
It does, however, support some remarkably short solutions.
John W. Harris and Harry O. Davis studied this board in the 1960's,
and found that most single vacancy to single survivor
problems
can be solved in 15 moves, with a few cases requiring 16 moves.
 This board appears on the earliest known
printed reference to peg solitaire, an engraving dated 1697.
This board is not a null-class board, therefore no
complement problem is solvable on it.
There are ten single vacancy to single survivor problems
solvable on this board, and
each can be solved in 20 or 21 moves.
This board appears on the earliest known
printed reference to peg solitaire, an engraving dated 1697.
This board is not a null-class board, therefore no
complement problem is solvable on it.
There are ten single vacancy to single survivor problems
solvable on this board, and
each can be solved in 20 or 21 moves.
 If you are solving a problem by hand, the best technique to use
(on any board) is to decompose it into block removals.
Note that the French board decomposes nicely into L and 3-removals
as shown in the figure on the right.
In order to solve a particular problem, one can modify this diagram
with appropriate starting and ending moves, as shown in the figures on the left.
If you are solving a problem by hand, the best technique to use
(on any board) is to decompose it into block removals.
Note that the French board decomposes nicely into L and 3-removals
as shown in the figure on the right.
In order to solve a particular problem, one can modify this diagram
with appropriate starting and ending moves, as shown in the figures on the left.


 In each diagram, the location of the starting hole is marked by an "S",
and the finishing hole by an "F".
After dividing the board up into block removals,
one must also check that the catalyst needed by each block removal
is present.
The sequencing of the block removals is indicated by the numbering.
If you don't understand how to turn such a diagram into a solution,
read the introduction to block removals at
In each diagram, the location of the starting hole is marked by an "S",
and the finishing hole by an "F".
After dividing the board up into block removals,
one must also check that the catalyst needed by each block removal
is present.
The sequencing of the block removals is indicated by the numbering.
If you don't understand how to turn such a diagram into a solution,
read the introduction to block removals at  This board is also known as "the Continental Board".
This is not a null-class board, and there are only
four single vacancy to single survivor problems
solvable on it (as shown in [B1]).
This board is very difficult to play on because it has 16
corners,
but this is really a significant constraint on play.
All four single vacancy to single survivor problems on this board
can be solved in 26 moves, but no fewer.
Look here
to view some solutions.
This board is also known as "the Continental Board".
This is not a null-class board, and there are only
four single vacancy to single survivor problems
solvable on it (as shown in [B1]).
This board is very difficult to play on because it has 16
corners,
but this is really a significant constraint on play.
All four single vacancy to single survivor problems on this board
can be solved in 26 moves, but no fewer.
Look here
to view some solutions.

 This board is null-class but is not
square-symmetric
(only rectangular-symmetric).
It is a draughtsboard created from an 8x8 square
board,
and a convenient way to play this board is using a checkers board,
playing only on the squares of one color with diagonal jumps.
In fact this board is identical to a standard checkers board,
just rotated 45 degrees, as the figure on the right shows.
This board is null-class but is not
square-symmetric
(only rectangular-symmetric).
It is a draughtsboard created from an 8x8 square
board,
and a convenient way to play this board is using a checkers board,
playing only on the squares of one color with diagonal jumps.
In fact this board is identical to a standard checkers board,
just rotated 45 degrees, as the figure on the right shows.

 Hoppers is a peg solitaire game invented by Nob Yoshigahara and marketed by
ThinkFun.
If you rotate this board 45 degrees, it is easy to see that it
is a 13 hole Diamond Board, or
draughtsboard created from a 5x5 square board,
with the addition of diagonal jumps along both diagonals.
Without the addition of diagonal jumps, no
single vacancy to single survivor problem
on this board is solvable.
However with the diagonal jumps many problems become solvable,
and its small size makes solutions easier to work out.
An interesting advanced problem is to try to solve the
central game on this board in as few as 7 moves.
Hoppers is a peg solitaire game invented by Nob Yoshigahara and marketed by
ThinkFun.
If you rotate this board 45 degrees, it is easy to see that it
is a 13 hole Diamond Board, or
draughtsboard created from a 5x5 square board,
with the addition of diagonal jumps along both diagonals.
Without the addition of diagonal jumps, no
single vacancy to single survivor problem
on this board is solvable.
However with the diagonal jumps many problems become solvable,
and its small size makes solutions easier to work out.
An interesting advanced problem is to try to solve the
central game on this board in as few as 7 moves.
 This is one of the first boards to appear in print, in 1779 by J. C. Wiegleb.
It has since been almost totally ignored. It is a null-class board, and
also a
Generalized Cross Board (see below).
There are 36 different single vacancy to single survivor
problems on it,
all of which are solvable except for the (4,0) or e1
complement problem.
This is one of the first boards to appear in print, in 1779 by J. C. Wiegleb.
It has since been almost totally ignored. It is a null-class board, and
also a
Generalized Cross Board (see below).
There are 36 different single vacancy to single survivor
problems on it,
all of which are solvable except for the (4,0) or e1
complement problem.

 The proof of the impossibility of the (4,0) or e1 complement is not a
simple matter, a brief outline of a proof is given in Beasley's book
The proof of the impossibility of the (4,0) or e1 complement is not a
simple matter, a brief outline of a proof is given in Beasley's book
 At first glance this null-class board doesn't seem very interesting.
You've seen one square board, you've seen them all, why not just quit at the
6x6?
However, unlike the 6x6, this square board does have a central hole,
which leads to more complexity in its solutions.
While all single vacancy to single survivor problems
are easy to solve using block removal methods,
this board supports some remarkably long sweeps.
A sweep of 34 is the longest geometrically possible,
shown on the board to the left.
What is more remarkable is that this particular sweep can be
reached from a single vacancy start.
At first glance this null-class board doesn't seem very interesting.
You've seen one square board, you've seen them all, why not just quit at the
6x6?
However, unlike the 6x6, this square board does have a central hole,
which leads to more complexity in its solutions.
While all single vacancy to single survivor problems
are easy to solve using block removal methods,
this board supports some remarkably long sweeps.
A sweep of 34 is the longest geometrically possible,
shown on the board to the left.
What is more remarkable is that this particular sweep can be
reached from a single vacancy start.




 There are a number of techniques and programming tricks that can speed up
the search for minimum length solutions.
Many of these are primarily computer science concepts,
and I will mention only those ideas specific to peg solitaire.
There are a number of techniques and programming tricks that can speed up
the search for minimum length solutions.
Many of these are primarily computer science concepts,
and I will mention only those ideas specific to peg solitaire.
 Most people will agree that solving the central game
on the standard 33-hole board is challenging.
In fact I once spent a weekend on this problem without success.
However I claim this just indicates approaching the problem by trial and error
(or exhaustive search) is very inefficient.
After you learn block removals (see [W2]),
the problem actually becomes quite simple.
It also seems that on any "well behaved" board, no matter how large, the
complement problem
should be relatively easy to solve using block removal methods.
An example of a well behaved board is any square board, but I believe
many other boards also fall into this category.
Most people will agree that solving the central game
on the standard 33-hole board is challenging.
In fact I once spent a weekend on this problem without success.
However I claim this just indicates approaching the problem by trial and error
(or exhaustive search) is very inefficient.
After you learn block removals (see [W2]),
the problem actually becomes quite simple.
It also seems that on any "well behaved" board, no matter how large, the
complement problem
should be relatively easy to solve using block removal methods.
An example of a well behaved board is any square board, but I believe
many other boards also fall into this category.
