This is an online vesion of my article published in the Journal of Unlikely Science (Smith. A. S, 2005). This research has generated considerable interest, sparking discussions in staffrooms worldwide, and I even discussed my findings live on BBC Radio.
The Affinities of Jaffa Cakes: Using Cladistics to Classify Biscuits
By Adam Stuart Smith
Abstract
A classification of biscuits is proposed, based on a scientifically sound
cladistic methodology. The most important factor in the broad classification
of biscuits is their shape, not the presence of absence of a chocolate coating,
as endorsed by previous phenetic classifications. Of perhaps the greatest
significance in this analysis is the unexpected confirmation that in a simple
dichotomising classification of cakes and biscuits, the Jaffa Cake is a
biscuit. As a logical solution, these results suggest that the implementation
of a three-way classification is necessary, including a new group of biscuit-cake
intermediates, the pseudobiscuits. This study may have much significance
in our every day lives, not only because of the novel terminology, but also
because of the link between government food classification and tax brackets.
Introduction
When Carolus Linnaeus first devised his classification of life in 1735,
there was no underlying phylogenetic justification. His system, like all
classifications biological or otherwise was ultimately a utilitarian tool
– simply put, a classification of life should be useful (Benton, 2000).
It is from this viewpoint, that I came to construct a concise classification
of another group of disparate objects, albeit a little less diverse than
life itself – the biscuits. Biscuits are not the first inanimate objects
to be subjected to taxonomic analysis. Mobile phones and volcanoes (Hone
et al. in prep) are other examples. Cladistics has also been applied to
those idiosyncratic cartoon characters, the Mr Men (Braddy pers comm. 2003).
Aims of the paper
The only other classification of biscuits, I am aware of, is given by Nicey
and Wifey (2004a). The scheme is constructed using simple phenetics. Although
the detailed interrelationships are not discussed, they give two broad types
of biscuits: [plain] biscuits and chocolate biscuits. These are each subdivided
into three smaller groups; entry level, midrange, and luxury. These categories
represent the increasingly complicated form and constitution of the biscuits.
This paper aims to test this taxonomic hypothesis using cladistic methods,
whilst illustrating the potential of this method for constructing other
classifications of everyday objects.
Materials and Methods
A cladistic analysis was performed to ascertain a scientifically valid and
robust classification of biscuits. A data matrix (Appendix 1) composed of
20 morphological characters (Appendix 2) and 20 biscuits and biscuit-like
snacks, was run through the computer program PAUP (Swofford, 2000) (phylogenetic
analysis using pastries?) (Heuristic Search, 1000 random replicates). The
simple sponge cake was chosen as a conservative outgroup and used to determine
the polarity of the characters. The resulting strict consensus tree is depicted
in fig 1.
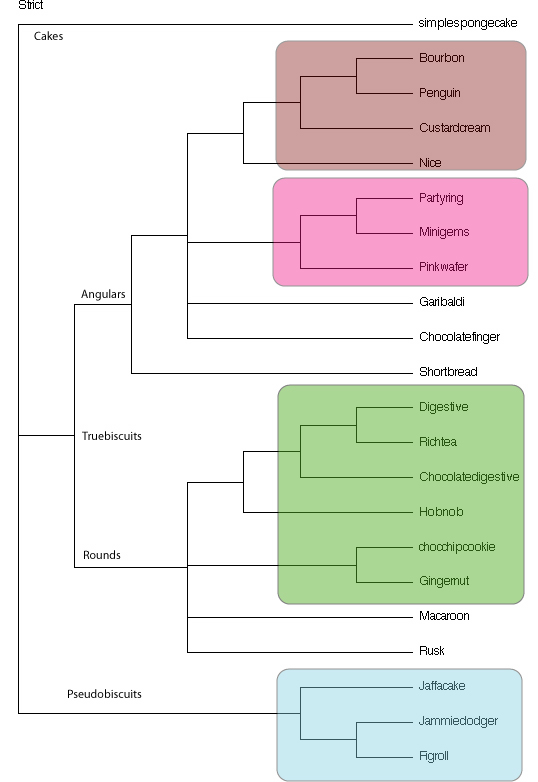
Fig 1. Cladogram of biscuits based on a cladistic analysis.
Discussion
Pseudobiscuits
The Jaffa Cake has long been a disputed member of the biscuit Order (Pootle,
2004).
In his report “Jaffa Cakes are Cakes - Proof from the Courtroom”,
Archibald (2004) describes a courtroom battle and the various evidences,
leading to the decision of the British Government to classify the Jaffa
Cakes as a cake, immunising Jaffa Cakes from VAT. Nicey and Wifey (2004b)
leave no doubt that the Jaffa is clearly a cake. The following response
is given on their website (Nicey and Wifey 2004a), to the frequently asked
question: “Are Jaffa Cakes biscuits?”
“No, no they're not. Apart from being called cakes they obviously
have a sponge base. Granted they appear to be some kind of luxury biscuit
being chocolate covered and shipping in a box.” [italics added].
The argument that the word ‘cake’ appears in the name is a simple
issue of semantics. Using this logic one may argue that shortcake is a cake.
Objects are classified based on their appearance. According to the current
analysis using parsimony, if the Jaffa Cake IS indeed a cake, then so are
Fig Rolls and Jammie Dodgers (an unarguable situation). This is because
these two biscuits show closer affinities with the Jaffa Cake than with
any other biscuits. So according to this classification, the Jaffa cake
IS a biscuit after all. It therefore seems there is no simple dichotomy
between cakes and biscuits. However, it is possible to make a compromise
between a biscuit and cake affinity for Jaffa cakes, by allocating this
group a new name. I propose the name Pseudobiscuits for this clade of three
genera, on account of their close kinship with both cakes and biscuits.
All other biscuits, can be referred to as ‘true biscuits’.
True biscuits
True biscuits split into two more or less equal sized groups, distinguished
by their shape: The Rounds and the Angulars. This indicates that shape is
a far more significant factor in classifying a biscuit than whether it is
chocolate covered or not (contra Nicey and Wifey, 2004a). However, there
is a clear transition within each group from simple to complex, confirming
the observations of Nicey and Wifey. The Rounds include, as their most simple
members, the rusk and similar forms. This group culminates in the well-known
dunking forms. Although double-layered Rounds are known, they are a rarity
and have been omitted from the current analysis. In contrast, the Angulars
acquired a greater variation in form and colour. Although most angulars,
such as the humble shortbread, retained a simple flat structure, some forms
exhibit extreme diversions from this condition, exhibiting exotic colours,
double-layers and fillings. The Penguin even dons an individual waterproof
wrapping. These angulars can be further subdivided into the families Partydae
(the children’s party biscuits) and the Bourbidae (the bourbons and
close relatives). The party biscuits include colourful members, such as
the pink wafer, and unusually for angulars, round party rings.
The Future
Future cladistic analyses should include many more genera of biscuits, and
more cakes, to confirm a comprehensive classification. Biscuits have a temporal
duration and origin, and it would be interesting to see if there are any
evolutionary patterns to the origin of biscuits There may also be a link
between the evolution of dinosaurs and biscuits, as suggested by Smith (2004).
There are obviously other ways of classifying biscuits, such as their respective
ingredients, but what this study shows, is that it is possible to approach
a classification from a more-or-less objective, rather than subjective standpoint.
Perhaps the governments should take note of this, when applying controversial
foods such as Jaffa Cakes, to tax brackets. Unfortunately, perhaps they
would be successful in their next attempt to add biscuit tax to the Jaffa
cake. If so, then…sorry folks!
Conclusion
A cladistic
analysis of biscuits shows that the biscuits can be classified as follows:
Pseudobiscuits: Jaffa Cake, Fig Roll, Jammie Dodger.
True biscuits:
Rounds: Digestive, Chocolate Digestive, Richtea, Hobnob, Choc-Chip Cookie,
Macaroon, Rusk, Gingernut.
Angulars: Shortbread, Chocolate finger, Garibaldi
Bourbidae: Bourbon, Penguin, Custardcream. Nice
Partydae: Partyring, Minigems, Pinkwafer
Acknowledgements
Thanks go to Hannah Maclellan, Becky Seeley, and Matt Williams for reviewing
early drafts of the manuscript, and to everyone who encouraged the publication
of this project.
References
Archibald, B. 2004. Jaffa Cakes are cakes: proof from the courtroom. http://www.educationet.org/messageboard/posts/38833.html
Benton, M. J. 2000. Stems, nodes, crown clades, and rank-free lists: is
Linnaeus dead? Biological Reviews 75, 633-648.
Hone, D. W. E., Mahony S. H., and Sparks, R. S. J. Cladistic analysis applied
to the classification of volcanoes. In prep.
Nicey and Wifey, 2004a. http://www.nicecupofteaandasitdown.com/biscuits/
Nicey and Wifey, 2004b. A nice cup of tea and a sit down. Little Brown Publishers,
192pp.
Pootle, D. 1999. Jaffa Cakes. http://www.bbc.co.uk/dna/h2g2/alabaster/A185104
Smith, A. S. 2004. Dinosaurs and their biscuits. http://www.geocities.com/dinobiscuits
Swofford, D. L. 2000. PAUP*: Phylogenetic analysis using parsimony (*and
other methods), version 4.0. Sinauer, Sunderland, Massachusetts.
??? 2004. Taxonomy of the mobile phone.
Appendix 1. Data matrix
Character/Genus 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
simplespongecake 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0
Bourbon 1 1 1 0 1 0 0 0 0 0 1 1 0 0 0 1 0 1 0 0
Digestive 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0 1
Chocolatedigestive 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 1
Richtea 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 1
Penguin 1 1 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 1 0 0
Custardcream 1 1 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0
Partyring 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0
Hobnob 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1
Jaffacake 0 0 0 1 1 0 1 0 0 0 0 0 1 0 1 0 1 0 0 0
chocchipcookie 0 0 1 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 1 0
Nice 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
Jammiedodger 0 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0
Figroll 1 1 0 0 1 0 1 0 0 0 0 0 1 1 1 0 1 0 0 0
Minigems 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0
Pinkwafer 1 1 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0
Shortbread 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0
Garibaldi 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
Chocolatefinger 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Macaroon 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 0
Rusk 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0
Gingernut 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0
Appendix
2. Characters, character descriptions, and character states.
1. Round/angular outline. Round = 0, angular =1
2. Single/double layer. Single = 0, double =1.
3. Colour pale/dark. Pale = 0, dark = 1.
4. Chocolate covering. Absent = 0, present = 1.
5. Filling. Absent = 0, present = 1.
6. Smooth/rough (Internal texture) Smooth = 0, rough =1
7. Fruit element (in any form). Absent = 0, present = 1.
8. Internal fenestra (hole in the middle as in party ring) Absent =0, present
=1
9. Psychodelic (pink or other bright colour), Absent = 0, present = 1
10. Individually wrapped. Absent = 0, Present = 1.
11. Dimples. Some biscuits show distinct rows of dimples on their surface
e.g. Bourbon. Absent = 0, present = 1.
12. Text. Absent = 0, present = 1
13. Thickness. Thin =0, thick =1.
14. Scenic surface. Smooth surface = 0, rough and rugged surface, =1.
15. Soft and spongey/crunchy. Soft =0, crunchy = 1.
16. Chocolate biscuit. Absent = 0, present = 1.
17. Fruit filling (differs from fruit element – must be a filling,
not isolated elements) Absent = 0, present = 1.
18. Cream filling. Absent = 0, present = 1.
19. Exotic/luxury element. Absent = 0, present = 1
20. Disc-like (very wide and flat e.g. round rich tea). Absent = 0, present
= 1.