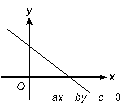
1. Which of the following statements about the straight line 3x
- 5y + 2 = 0 must be true?A. The slope of the line is negative. B. The line is perpendicular to 5x - 3y = 0.
C. The x-intercept is -1.5. D. The y-intercept is 0.4.
E. The slope of the line is
2. If the point (k, 6) lies on the line passing through the points (0, 0) and (-1, 3),
find the value of k.
3. Which of the following is/are correct about the straight line ax + by + c = 0
shown in the figure?
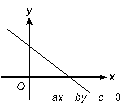
(I) slope > 0 (II) x-intercept < 0 (III) y-intercept > 0
A. (I) only B. (II) only C. (III) only D. (I) and (II) E. (I) and (III)
4. Find the equation of the straight line which passes through (-1, -2) and is parallel to 3x - 2y = 0.
5. If two lines 2x + y - 1 = 0 and x + ky + 1 = 0 are perpendicular to each other,
find the value of k.
6. If P (k - 1, k + 3) lies on the x-axis, find the coordinates of P.
A. (-4, 0) B. (4, 0) C. (0, -4) D. (0, 4) E. (2, 0)
7. If the distance between (k, 1 - k) and
(1 + k, 1) is ![]() , find the value(s) of k.
, find the value(s) of k.
A. 7 B. 3 C. 1 D. 1 or -1 E. 3 or -3
8. Find the equation of the line passing through (2, 5) with slope ![]() .
.
9. Find the equation of the line whose slope is ![]() and its y-intercept is 2.
and its y-intercept is 2.
10. For any value of m, the line y = mx + m passes through a point P.
Find the coordinates of P.
A. (0, 0) B. (0, 1) C. (0, -1) D. (1, 0) E. (-1, 0)
11. Which of the following is correct for the straight line ![]() as shown
below?
as shown
below?
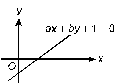
A. a = 0 or b = 0 B. a > 0 and b > 0 C. a > 0 and b < 0
D. a < 0 and b > 0 E. a > 0 and b > 0
12. Given A(1, -2) and B(-5, 6), find the coordinates of a point P
if B divides PA in the ratio 3 : 2.
A. (-14, 12)
B. (-14, 18)
C. (-11, 18)
D. ![]() E.
E. ![]()
13. If q and f are the inclinations of two perpendicular lines,
which of the following must be true?
A. q = f B. q f = 1 C. q + f = 90° D. q + f = 180° E. q - f = 90° or -90°
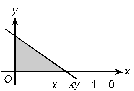
14. In the following figure, the straight line x + ky - 1 = 0 passes through the point (-2, 3).
Find the area of the shaded region.
15. Given three points A(-1, 4), B(x, 6) and C(3, -2) such that AC ^ BC.
Find the value of x.
16. The circle ![]() cuts the x-axis at the points P and Q.
cuts the x-axis at the points P and Q.
Find the length of PQ.
17. If the straight line x - 8 =
0 touches the circle ![]() ,
,
find the value of k.
18. If the equation of a circle is ![]() , which of the following
is/are true?
, which of the following
is/are true?
(I) The centre of the circle is (-3, -4).
(II) The radius of the circle is 5.
(III) The circle passes through the origin.
A. (I) only B. (II) only C. (III) only D. (I) and (III) E. (II) and (III)
19. If the area of the circle ![]() is 16p
, find the value of c.
is 16p
, find the value of c.
20. Find the equation of the circle passing through the points (0, 0), (1, 2) and (-1, 3).