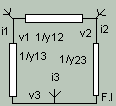
Simplified Simulation Of Analog Electronic Circuits.

The (floating) admittance (inverse impedence) matrix of a circuit is best illustrated by an example: Figure I is a simple resistive network. To avoid complication, in this particular example, the nodes are arbitrarily numbered and node 0 is left floating (unconnected.) However, this in general will not be the case. Because charge is neither created nor consumed inside a node, the total current into any node is zero. Nevertheless, it is still useful to write down an expression for them. If the currents (rather than the voltages) are the dependent variables, and assuming linearity:

i1 = (v1-v2)y12 + (v1-v3)y13

i2 = (v2-v1)y21 + (v2-v3)y23

i3 = (v3-v1)y31 + (v3-v2)y32

or, rearranging, i = yv

[i1]		[y12+y13	-y12	-y13]		[v1]
[i2]	=	[-y21	y21+ y23	-y23]	x	[v2]
[i3]		[-y31	-y32	y31 + y32]		[v3]

Now eliminate v3 from all higher equations by the substitution v3 = ( v1y31 + v2y32 ) / (y31 + y32 ). (If more nodes had been present, the additional voltages would have been eliminated iteratively.) Hence, the circuit has been reduced to a two-port network, figure II. If nodes 0, 1 and 2 are always the input, output and earth nodes respectively, it can be shown that:

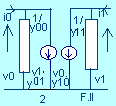
i0 = y00v0 + y01v1

i1 = y10v0 + y11v1

The voltage gain Av is v1 / v0 = -y10 / ( y11 + yL )

the current gain Ai is i1 / i0 = y10yL / ( Dy + y00yL)

the input impedance zi is v0 / i0 = ( y11 + yL ) / ( Dy + y00yL )

the output impedance zo is v1 / i1 = ( y00 + ys ) / ( Dy + y11ys )

where ys is the source admittance, yL is the load admittance and Dy = y00y11 - y10y01

The admittance matrix of any linear circuit can be formed by inspection:

yab is minus the total admittance seen between nodes a and b.

ybb is the total admittance connecting to node b.

Clearly, for passive components (resistors, coils and capacitors), yab=yba.

Because charge is conserved, the sum of any row or column must be zero. (This includes active devices as well.)

The matrix for a transistor is given below. For low frequency work, yre and yoe are usually ignored. yfe is Ie (mA) / (25 mV) approximately, so if (for example) Ie =1 mA, yfe is 1 / (25 Ohms), while yie is yfe / hfe ; therefore if, in addition, hfe = 300 yie = 1 / (300.25 Ohms) = 1 / (7500 Ohms). However, a good design should not depend on the exact value of hfe.

	B	C	E
B	yie	yre	-yie-yre
C	yfe	yoe	-yfe-yoe
E	-yie-yfe	-yre-yoe	s

s being yie + yfe + yre + yoe

Notes:

In signal terms, all power supply connections are commoned. (This is not to say that the admittance matrix method cannot be used to obtain the DC bias - the quiescent point- of a circuit. However, the transistor YFE is now IE (mA) / 650 milliVolts approximately - for silicon bipolar transistors. Starting from a guess value, it will require a few iterations before the actual transistor current values are obtained. If more than one power supplies are used, they need to be considered one at a time, and the results combined using superposition.)
Oscillators can be evaluated by breaking the loop. The group delay d ( phase ) / dw will require a second calculation very close to the frequency of interest.
The steady- state time response to a non- sinusoidal signal can be determined by splitting it to its Fourier components and adding the corresponding responses.
Most circuits will contain some inductance or capacitance, so some of the y parameters, gains and two-port impedences will be compex numbers (frequency- variable.) A procedure to reduce that matrix follows (for the nodes numbered 0 to n% inclusive; yr is the real part of the matrix, yi the imaginary, y = yr +j yi .) Sparse matrix techniques could be used to enhance processing and storage.

                   FOR x% = n% TO 3 STEP -1:

                    a=yr(x%,x%)^2 +yi(x%,x%)^2:

                    FOR p% = 0 TO x%-1:

                     FOR q%=0 TO x%-1:

                      b=yr(p%,x%)*yr(x%,q%)-yi(p%,x%)*yi(x%,q%):

                      c=yr(x%,q%)*yi(p%,x%)+yr(p%,x%)*yi(x%,q%):

                      yr(p%,q%) = yr(p%,q%)-(b*yr(x%,x%)+c*yi(x%,x%))/a:

                      yi(p%,q%)=yi(p%,q%)-(c*yr(x%,x%)-b*yi(x%,x%))/a:

                     NEXT q%, p%, x%

Example: A very short (but also extremely thin) wire is intended to carry very high frequency signals. The distributed line resistance, Rd is 100 Ohms and the distributed line capacitance (to earth), Cd is 10 pF.

The load impedance is negligibly high, in comparison, and the nominal value of the corner frequency, f_t is just under 160 MHz. The wire is modelled by a combination of lumped elements (whose number is variable), fig 2b. It does not look productive to use more than about 10 elements. The following graph shows the input impedence, z_i, at 160 MHz, in modulus and argument form, against the number of elements used: 1 through 35 (the horizontal axis is logarithmic.)

Did you want to check calculations, or a subroutine, of your own? Using one element, at 160 Mhz, the voltage gain in deciBels is (20logAv) or -3.04 dB's and the phase angle is -46^o (negative, since the current leads the voltage.) The input impedence is 141 Ohms at -44^o (capacitive) and the output impedance is 70 Ohms/ -45^o. For the sake of those calculations, the source impedance is negligibly low.

A word of caution is in order: Simulation does save tedious arithmetic, (especially if complex numbers are involved), and will reveal some of the obvious design errors (even to someone not conversant with analogue circuitry.) However, simulators provide data for all circuits, (including ones which are not good) and there is definitely more to analogue design than obtaining the proper figures from a simulator: For example, interference must be avoided, and a clever ground layout adopted when actually implementing the design on a pcb.

Reference: Wireless World magazine (British) Volume 86, February issue, p.39