Transforms using non-orthogonal components
Transforms to the frequency domain usually involve normalised and orthogonal components. Results are interpreted more easily if the components are normalised, so this is largerly a matter of convenience. Orthogonality, on the other hand, is far more serious: It implies that coefficients can be derived by correlation, rather than solving a system of linear algebraic equations, and makes the problem quadratic, rather than cubic, in the number of samples. The orthogonality restriction is not entirely inescapable, though, and sometimes it is even desirable not to constrain components to be uncorrelated.
Of transforms, there is no shortage: The Fourier Transform is more appropriate analytically. With numerical data sets, the Walsh transform gives accurate results, and requires few calculations. Wavelet transforms are used by some researchers for signal processing purposes. The Haar transform, in particular, emphasises high frequency components.
The ‘jpeg’ standard for image compression either quantises high frequency components using a smaller number of bits, or ignores them altogether. Surely, this is ample evidence that focus must be placed on low sequency components. The following diagram presents one possibility (for 8 components): I do not know the name of this transform.
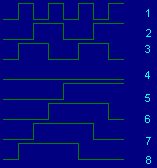
Clearly, (5) and (7) are not orthogonal to (6) or (8). The effect is the partial reconstruction of a data set must be subtracted from it before calculating the coefficient of the next (non-orthogonal) component, by correlation. The fact that the coefficients depend on the order of calculating components, is surely a disturbing notion to anybody who is mathematically inclined. However, anybody interested in image compression, will probably not mind whether the transform of a data set is unique. It is true that improved inverse transform results can be obtained by repeating the direct transform calculations, giving precedence to those non-orthogonal components whose coefficients have a larger magnitude.
The transformation of the triple period wave was expected with interest (the triple period is not present in the components): According to the initial phase, there are 3 possible placements: After shuffling non-orthogonal coefficients, the 'balanced' placement was reproduced exactly; the symmetric placements were 20% and 33% in error after reconstruction. Random noise was also modelled (ten batches), and the average error was just under 11%. In the following figure is shown the same data set modelled by Fourier components in the Walsh section (the reconstruction using the low sequency biased transform is in green):

It seems that the Walsh transform is a clear winner: An error of about 11% has been introduced by favouring low sequency (non-orthogonal) components, and an improvement, if it is attained, will only involve additional calculations. However,
- the wisdom of exactly modelling random noise (on a rough surface) is debatable
- a more realistic comparison (for compression purposes) can be made after the major components only have been retained.
It may be useful to repeat calculations after only the major components have been retained, in order to improve accuracy. A demonstration program for this section is given. It involves integer arithmetic, so if the samples' magnitude is under 10 or thereabouts, it is best to switch to floating point arrays.
Concentrating on low sequency components implies that the boundary between two objects, or an object and the background, will be reproduced faithfully by retaining a single component (plus the average value of the row.) An image compression scheme based on these ideas will be presented soon enough.


