Poonam Sikka, A. Mary Selvam, A.S. Ramachandra Murty and Bh.V. Ramana Murty
Indian Institute of Tropical Meteorology, Pune-411 008, India
Email: selvam@tropmet.ernet.in
Website: http://www.geocities.com/CapeCanaveral/Lab/5833
1. INTRODUCTION
Recent experimental investigations relating to the electrical coupling
between the troposphere, ionosphere and magnetosphere suggest the possible
solar modulation of atmospheric electrification. Analysis of the 1200 hrs
of stratospheric balloon data has indicated correlation between the vertical
electric field and the magnetic activity parameters (D’Angelo et al., 1982).
Markson (1978) has observed correlation between the earth-ionospheric potential
variations deduced from airplane soundings and the solar wind parameters.
Evidence suggests that higher solar wind speeds yield higher potential
differences. Holzworth and Mozer (1979) from the study of the stratospheric
balloon data obtained during the August 1972 solar flare have concluded
that the solar proton shower occurred during the event ‘compressed’ the
ionosphere down to a level below 30 km. The solar proton fluxes
have been found to be correlated with a decrease in the local vertical
field component near 30 km. The above observations provide the evidence
for the downward coupling of high altitude processes into the middle atmosphere
and the troposphere. Similarly upward coupling of the tropospheric processes
into the middle atmosphere has been noticed from the following observations.
Balloon data in the stratospheric region display classic fair weather vertical
electrical field magnitudes modulated by the solar wind effects (Kelly,
1983). During the thunderstorms large enhanced fields are seen in the horizontal
components as well as large and reversed vertical fields (Holzworth, 1981).
Direct coupling of discharge electric field into the ionosphere have been
recently detected in a multiple platform (three rockets, a stratospheric
balloon, an airplane and ground-based detectors) during a thunderstorm.
Numerous electrical discharges have been recorded simultaneously by all
the sensors located in different platform. Transient fields of tens of
mV m-1 have been observed in the mesosphere and the ionosphere.
Large transient fields have been seen at stratospheric heights.
In this paper a physical mechanism for the electrical coupling of the
troposphere, ionosphere and the magnetosphere has been discussed along
with the results of analysis of atmospheric electrical field for Colaba,
Bombay (8 53’ 56"N, 72 48’ 54" E, 9.8
m asl) and geomagnetic data (DST index, Ap
index and MSB crossing dates) for the 31 year period from 1936-1966.
Based on the above theoretical and observational results possible solar
modulation of atmospheric electrification has been investigated.
2. PHYSICAL MECHANISM
A gravity wave feedback mechanism for the troposphere - ionosphere coupling
has been proposed (Mary Selvam et al., 1982, 1984a). Vertical mass exchange
in the troposphere-ionosphere-magnetosphere takes place through a chain
of eddy systems. Any perturbation in the troposphere would be transmitted
to ionosphere and vice versa. A global perturbation in ionosphere, as the
one caused by solar variability, is transmitted to troposphere influencing
weather systems/geomagnetic/atmospheric electrification processes.
The atmospheric boundary layer (ABL) contains large eddies (vortex
rolls) which carry on their envelopes turbulent eddies of surface frictional
origin (Fig.1). It is shown that the buoyant production of energy by microscale-fractional-condensation
(MFC) in turbulent eddies is responsible for the sustenance and
growth of large eddies (Mary Selvam et al., 1983b). The circulation speed
of the turbulent eddy according to the following expression.
where W and w are respectively the r.m.s. circulation
speeds of the large and turbulent eddies and R and r their
respective radii. The buoyant production of turbulent energy by the MFC
process is maximum at the crest of the large eddies and results in the
warming of the large eddy volume. The turbulent eddies at the crest of
the large eddies are identifiable by a microscale-capping-inversion (MCI)
which rises upwards with the convective growth of the large eddy in the
course of the day. This is seen as the rising inversion of the day time
ABL
in the echosonde records.
Fig. 1
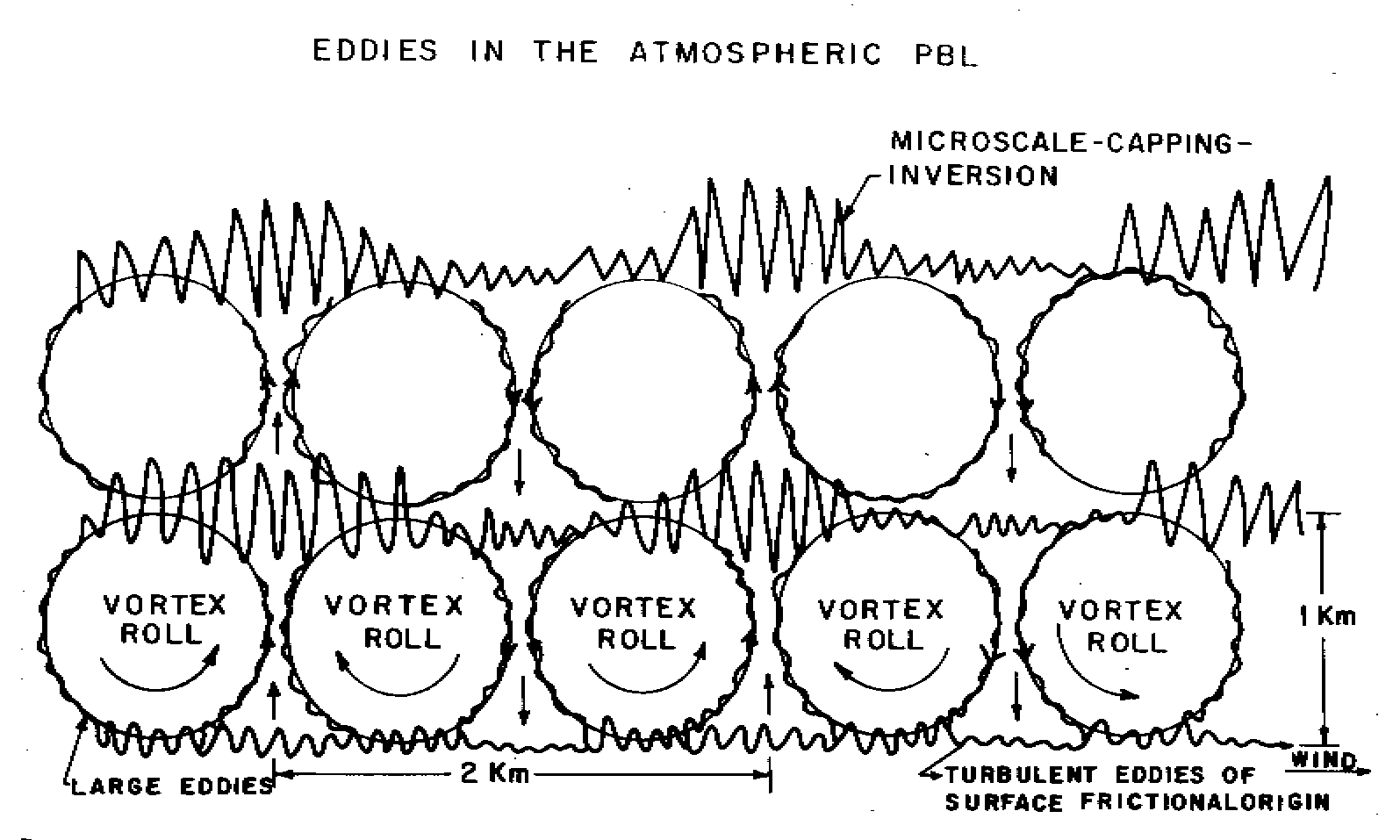
As the parcel of air corresponding to the large eddy rises in the stable
environment of the MCI, Brunt Vaisala oscillation are generated
(Mary Selvam et al., 1983a, 1984b). Thus the large eddy growth is associated
with generation of a continuous spectrum of gravity (buoyancy) waves in
the atmosphere. The slopes of temperature and wind spectra were theoretically
shown to be equal to - 1.8 for the eddy scale ratio (Z) i.e.
R/r
= 10 (Mary Selvam et al., 1984c) and it is in agreement with the
observed spectral slopes in the troposphere-stratosphere-ionosphere-magnetosphere
(Weinstock, 1980, Dewan, 1979, Keskinen et al., 1980, Tsurutani et al.,
1981, Carter and Balsley, 1982, Van Zandt, 1982).
2.1 Vertical Mixing
The dilution by environmental mixing of the large eddy volume by turbulent
eddy fluctuations across unit cross-section of the large eddy surface is
derived as follows.
The ratio of the upward mass flux of air in the turbulent eddy to that
in the large eddy across unit cross-section per second is equal to
w*
/
dW. where
This fractional volume dilution of the large eddy occurs in the environment
of the turbulent eddy. The fractional volume of the large eddy which is
in the environment of the turbulent eddy where dilution occurs = r/R.
Therefore, the total fractional volume dilution k of the large eddy per
second across unit cross section can be expressed as
The value of k = 0.4 when R/r = 10 since dW = 0.25w* (Eqn.1).
In Equation (2), dW is the increase in vertical velocity of the
large eddy per second as a result of w*. The height interval
in which this incremental change in the vertical velocity occurs is dZ
which is equal to r (Fig.2).
Fig. 2
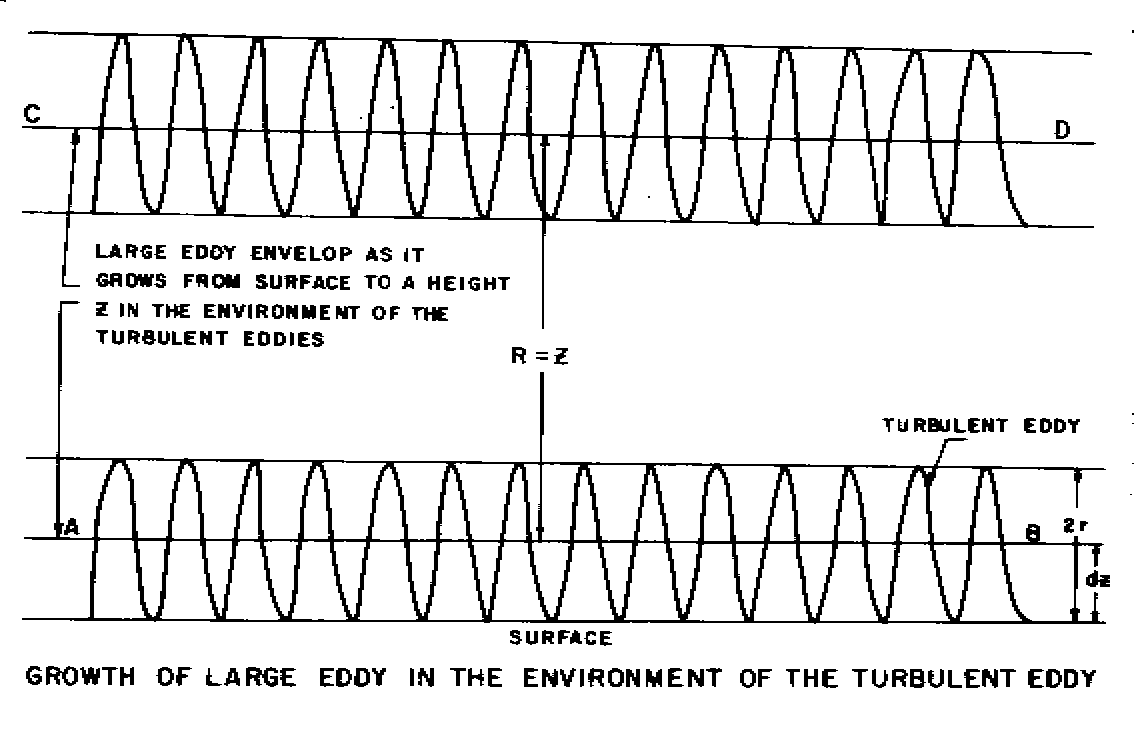
Using the above expressions Equation. (2) can be written as follows
Integrating Equation (3) between the height interval r and R
the following relation for W can be obtained.
In the above expression for W it is assumed that w*
is constant for the height interval of integration.
A normalised height Z with reference to the turbulence scale
r
can be defined as
Using the above expression Equation (4) can be written as follows :
The value of k is constant for a fixed value of R/r. As defined earlier k represents the fractional volume dilution rate of the large eddy by turbulent eddy fluctuations across unit cross-section on its envelope and is constant for a fixed value of the scale ratio Z.
It is well known from observations and from existing theory of eddy
diffusion (Holton, 1979) that the vertical wind profile in the atmospheric
ABL
follows the logarithmic law which is identical to the expression shown
in Equation. 6. The constant k for the observed wind profile is
called the Von Karman constant. The value of k as determined
from observations is equal to 0.4 and has not been assigned any
physical meaning in the literature.
The new theory relating to the eddy mixing to the ABL proposed
in the present study enable to predict the observed logarithmic wind profile
without involving any assumption as in the case of existing theories of
eddy diffusion processes. Also it is shown that the Von Karman constant
is associated with a specific physical process. It is the fractional volume
dilution rate of the large eddy by the turbulent scale eddies for the scale
ratio of 10.
Identifiable large eddies can grow in the atmospheric ABL only
for scale ratios Z ³ 10 since
for smaller scale ratios the volume dilution rate by turbulent eddy mixing
is more than 0.5. The convective scale eddy of radius Rc
evolves from the turbulence scale eddy of radius r for scale ratio (Z)
i.e., Rc/r = 10. This type of successive decadic
scale range eddy mixing generates the convective, meso-, synoptic- and
planetary scale eddies starting from the turbulence scale as the basic
unit (Mary Selvam et al., 1984c).
Observational evidence for the tropospheric eddy chain link up with
ionosphere is seen in satellite observations which indicate that increased
currents at ionospheric levels are accompanied by a simultaneous increase
in wind speed at lower levels. Measurements with Poker Flat radar and instruments
at Alaska and with NOAA radar at Fairbanks support this contention.
From the motions of chemically released ions and neutral clouds it is apparent
that neutral winds in the high latitude ionosphere are driven principally
by ion drag forces. Observations of infrasonic waves following sudden ionization
enhancements indicates the existence of momentum transfer (Heppner, 1975).
Carter and Balsley (1982) have reported correlation between short term
fluctuations in the wind field near the mesopause (~ 83 - 90 km)
and the intensity variations of the auroral electrojet (~110-115
km)
2.2 Troposphere - Ionosphere coupling
It is postulated that a vertical chain of eddy system exists in the
atmosphere with the convective scale as the smallest unit (Fig.1). Turbulent
eddies of surface frictional origin ride on the envelopes of these convective
scale eddies and reach upto ionospheric levels.
This stack of convective scale eddies will be associated with microscale-capping-
inversion layers at intervals equal to the convective scale size, i.e.
2
Rc
(2-20 km). The layered structure of the atmospheric
PBL with
thin sheets / layers of turbulence has been observed by aircraft, echosonde,
MST radars throughout the atmospheric PBL extending up to
ionospheric levels (Gage, 1979, Carter and Balsley, 1982).
This vertical stack of convective scale eddies result in vertical mass
exchange throughout the column extending from the surface to the inospheric
levels. This upward propogation of convective scale eddies derives energy
from (i) microscale-fractional- condensation process in the turbulent eddies
and (ii) the exponential decrease of atmospheric density with height. In
the upper troposphere and up to ionospheric levels the eddy amplification
occurs as r
-1/2 where r
is the atmospheric density (Beer, 1975).
The vertical mass exchange between surface to ionospheric levels by
the eddy stack is the coupling mechanism which transmits solar activity
controlled variation of the ionosphere to the lower troposphere and thus
influence the weather systems and other atmospheric process.
2.3 Observational Evidence for the Vertical Eddy Chain
Weinstock (1981) has shown that the energy dissipation rate e
of turbulence in the stable free atmosphere can be expressed by the following
relation :
![]() is the variance
of the vertical velocity and NB the Brunt-Vaisala frequency.
Observations indicate that the above relation for e
holds good for the atmospheric PBL up to the stratosphere. The new
theory of atmospheric eddy mixing can be used to derive the relation as
follows :
is the variance
of the vertical velocity and NB the Brunt-Vaisala frequency.
Observations indicate that the above relation for e
holds good for the atmospheric PBL up to the stratosphere. The new
theory of atmospheric eddy mixing can be used to derive the relation as
follows :
The dominant eddies in the atmospheric PBL are in the Brunt-Vaisala
eddies since they are generated and sustained by the microscale-fractional-condensation
process in the turbulent eddies.
Let WB = root mean square value of the vertical velocity
of the large eddy i.e., for one complete cycle of the large eddy oscillation.
Let NB = Brunt-Vaisala frequency associated with
the large eddy.
Thus e , the dissipation rate per
second of the vertical velocity variance associated with the Brunt-Vaisala
eddy is given as follows :
The value of k = 0.4 for size ratio Z = 10.
Thus the predicted relation for e at
Equation.8 is identical to the observed relation for e
at Equation.(7) providing proof for the existence of a vertical eddy chain
with convective scale as the basic unit.
3. ATMOSPHERIC ELECTRIC AND GEOMAGNETIC FIELDS
In the following it is shown that the atmospheric electric field and
geomagnetic field variations are also manifestations of the vertical mass
exchange process between the lower troposphere and ionosphere.
The vertical mass exchange on the sunlit hemisphere gives rise to upward
transport of surface air. The nuclei in the surface air layers contain
a net positive space charge and thus there is a aerosol current
ia* in the upward direction from the surface layers which
is expressed as
ia* = w* s*
s *= net positive space charge density in the surface layer.
As the large eddy grows there is upward transport of net positive space
charge from surface layers the concentration decreasing with height due
to dilution of the large eddy volume by turbulent mixing as explained earlier.
The fractional mass flux f of the surface air in the vertical
can be derived as follows: Across unit cross-section of the large eddy
surface at normalised height z the ratio of the upward mass flux of air
to the upward mass flux at surface level = W/w*. This
excess upward mass flux occurs in the environment of the turbulent eddy
and hence the fractional volume of the large eddy associated with this
dilution = r/R = 1/Z. Hence the fractional mass flux f of
the surface air at normalised height Z is given as
![]()
Earlier (Equation.6) it was shown that the wind profile of the large
eddy is logarithmic with height.
f gives the fractional upward mass flux of surface air at any
level Z across unit area.
Under steady state conditions a fraction f of surface air will be found at normalised height Z.
The atmospheric nuclei and thus space charge concentration originate
from the surface layers. Thus the net positive space charge concentration
s
as follows :
The atmospheric electric field F at any level is given as
where s
is
the net positive space charge density at the level. F and s
are expected to decrease with height according to the f distribution
(Eqn.9). The vertical profile of f is shown in Fig.3 and it is similar
to the observed F and nuclei profile (Imyanitov and Chubarina, 1967)
in the atmospheric (Fig.4). The value of f has been computed assuming
that the dominant turbulent eddy radius (r) is equal to 100m
and lm respectively above and below the lifting condensation level
(LCL).
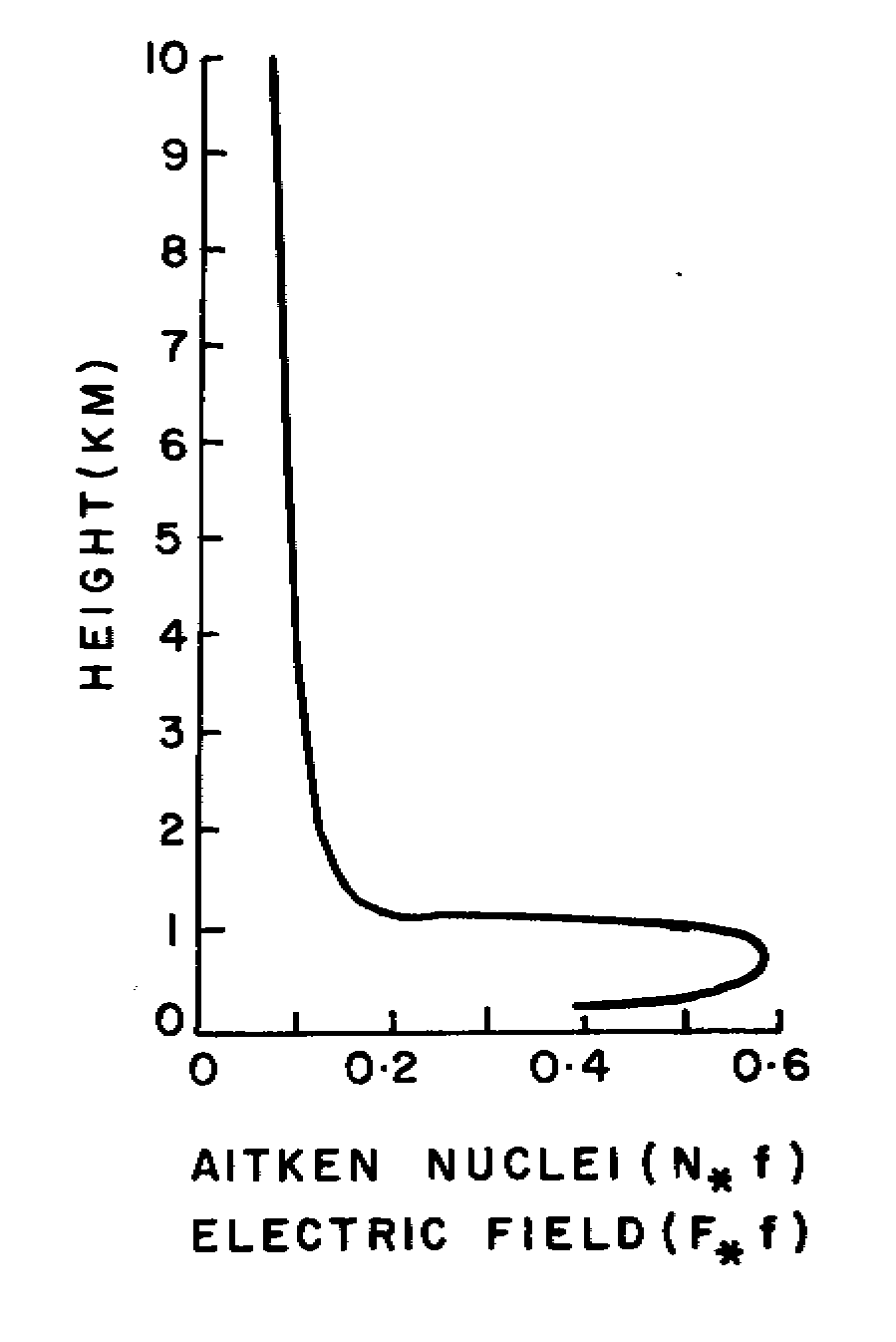
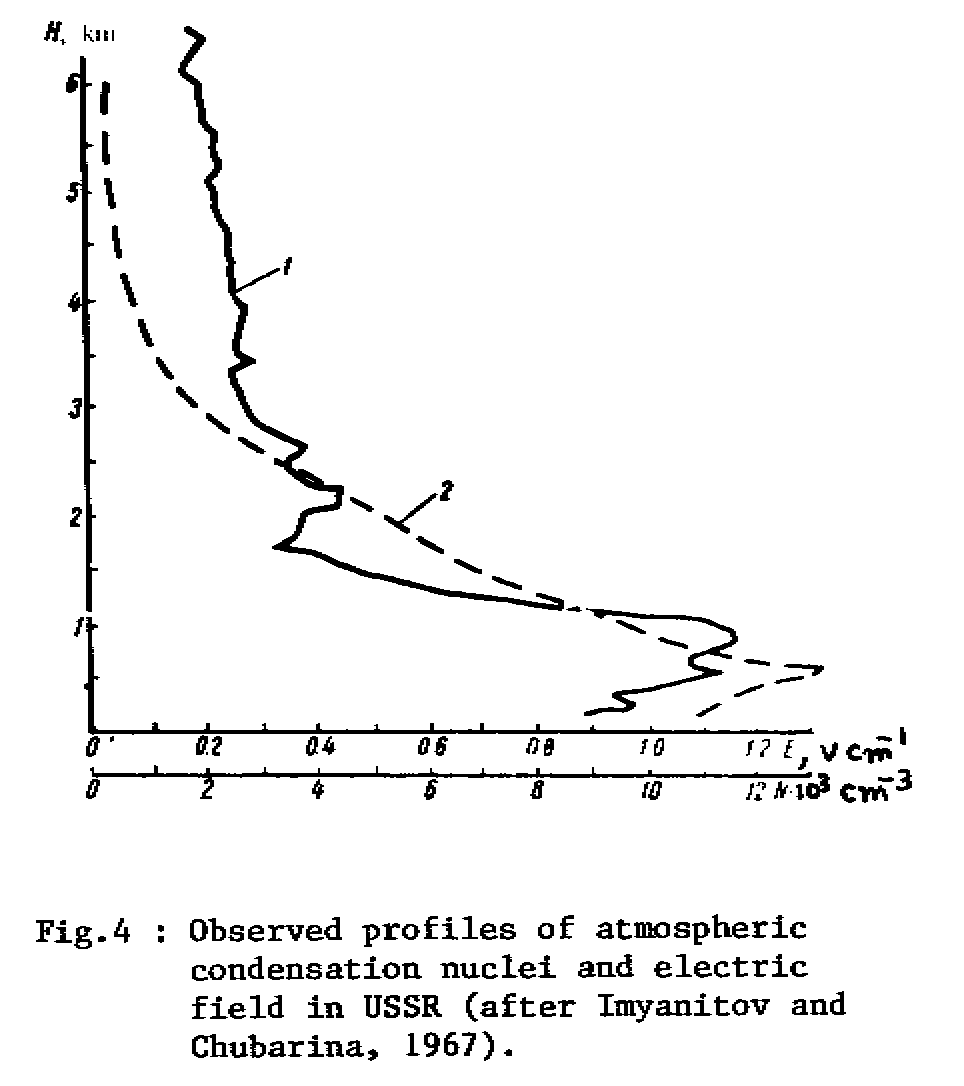
The aerosol current at any level Z is given by
ia = s * f Z w* f Z
Thus the aerosol current ia produced
by the vertical mass exchange generates the observed atmospheric electric
field. The conventional air-earth conduction current cannot discharge the
atmospheric electric field thus produced since the dynamic charge transport
by the vertical mass exchange process is faster than the ion mobilities
by more than one order of magnitude.
The vertical distribution of the aerosol current ia
follows the f2Z2
distribution.
The convective scale ( 2 km2) aerosol current can
be computed and shown to be 105 times larger and is in
opposite direction to the conventional air-earth conduction current from
Equation.12. The vertical aerosol currents are of the right order of magnitude
and direction as those of the vertical currents postulated to exist in
the atmosphere by Bauer (1920) and Schmidt (1924) in their hypothesis for
explaining the variations in the H component of the global geomagnetic
field. The aerosol currents occur over convective scale i.e., 1
km2 and thus were not detected by conventional spot observations.
Lanzerotti et al., (1982) found the fluctuations with periods less than
one day in the powering voltage on a transatlantic cable which are predominantly
produced by fluctuations in the geomagnetic field. Enhancements at similar
frequencies are seen in both voltage and magnetic field spectra. These
observations corroborate the hypothesis proposed in this paper.
The results of the analysis of the surface electric field data for Colaba
for the period 1936-66 are discussed below.
(a) Interplanetary Magnetic Field (IMF) and Electric field.
The results of the harmonic analysis of the electric field data showed
a fundamental peak with a period of 6 to 7 days. This period corresponds
to the average time interval between any two successive MSB crossing events.
Periodicities of 12-15 days and 21-23 days are also present
in the electric field. The peaks in the negative DST
index occurred when maximum values of the positive electric field are present.
Results of the cross-spectral analysis of the electric field data and the
daily mean equatorial DST index suggested negative correlation
between electric field and IMF for all significant wave lengths
less than 30 days with maximum being centred around 27 days,
which may roughly correspond to one solar rotation period. A positive correlation
between surface electric field and IMF is found in the wave length
range 35-55 days with maximum at about 47 days. This appears
to correspond with two solar rotation periods. The results indicate a strong
association between surface electric field and IMF.
(b) Geomagnetic Storms and Electric Field
Results of the analysis of the electric field, major geomagnetic storms
(with Ap>100) and the selected meteorological
parameters (surface pressure, wind, humidity, temperature and rainfall)
indicate the following. Geomagnetic storms are followed by a decrease in
the electric field during a 6-day period following the date of occurrence
of the storm. During the summer monsoon (June-September) geomagnetic storms
are followed by a decrease in surface pressure, increases in wind velocity
and rainfall. The results of the study corroborate the hypothesis that
there is a two way interaction between the ionospheric SQ
current systems and the meteorological parameters i.e., a geomagnetic storm
in association with a major solar flare can enhance the vertical mass exchange
resulting in enhancement of existing weather systems. This in turn feeds
back energy into the SQ current system which is manifested
as a delayed geomagnetic storm (sub-storm) following the solar flare induced
sudden storm commencement (SSC).
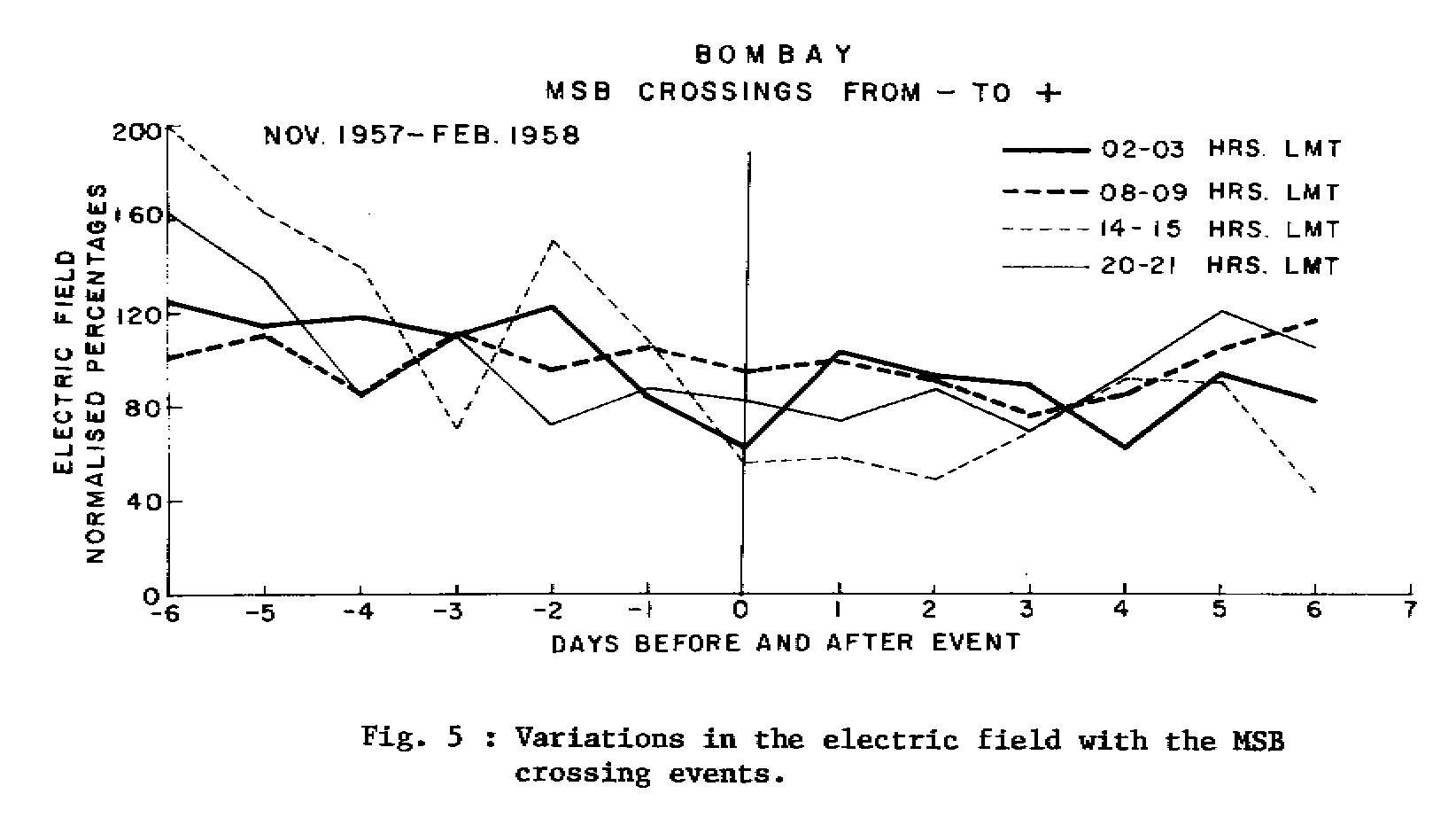
(c) Interplanetary Magnetic Sector Boundary (MSB) Crossing Events and Electric field.
The results indicate that an MSB crossing for which there is
a negative to positive polarity change is associated with a decreasing
surface electric field for a total period of about 4 days inclusive
of the MSB crossing date (Fig.5). An MSB crossing event for
which the polarity changes from positive to negative is associated with
a distinct peak in the surface atmospheric electric field within 2
days of the MSB crossing event. The above results are in agreement
with those reported by other investigators (Herman and Goldberg, 1978).
REFERENCES
Beer, T., 1975 : Atmospheric Waves, Adam Hilger, London, pp. 300.
Carter, D. A. and B.B. Balsley, 1982 : The summer wind field between
80 and 93 km observed by the MST radar at Poker Flat, Alaska (65oN),
J. Atmos. Sci., 39, 2905-291.
D’Angelo, N., I.B. Iversen and M.M. Madsen, 1982 : Influence of the
daun-dusk potential drop across the polar cap on the high-latitude atmospheric
vertical current, Geophys. Res. Letts.9, 773-776.
Dewan, E.M., 1979 : Stratospheric wave spectra resembling turbulence.
Science, 204, 832-835.
Gage, K. S., 1979 : Evidence for a K-5/3 inertial range in
mesoscale two-dimensional turbulence. J. Atmos. Sci., 36, 1950-1954.
Heppner, J.P., 1975 : High-latitude ionospheric winds related to solar-interplanetary
conditions. In ‘Possible relationships between solar activity and meteorological
phenomena’ National Aeronautics and Space Administration Report, Washington
D.C., pp. 360.
Holton, J. R., 1979 : An introduction to dynamic meteorology, Academic
Press, New York, pp. 391.
Holzworth, R.H. and F.S. Mozer, 1979 : Direct evidence of solar flare
modification of stratospheric electric fields. J. Geophys. Res., 84, 363-367.
Imyanitov, I. M. and E.V. Chubarina, 1967 : Electric of the free atmosphere.
Israel Program for Scientific Translations, Jerusalem, pp. 212.
Kelley, M.C., 1983 : Middle atmospheric electro-dynamics, Reviews of
Geophysics and Space Physics, 21, 273-275.
Keskinen, M.J., S. L. Ossakov and B.E. McDonald, 1980 : Non-linear evolution
of diffuse auroral F-region ionospheric irregularities. Geophys. Res. Letts.,
7, 573-576.
Lanzerotti, L.J., A. Meloni and L.V. Medford, 1982 : Induction in a
transatlantic cable at periods between 20 minutes and one day, Geophys.
Res. Letts., 9, 439-441.
Markson, R., 1978 : Solar modulation of atmospheric electrification
and possible implications for the sun-weather relationship, Nature, 273,
103-109.
Mary Selvam, A., G.K. Manohar, S. S. Kandalgaonkar, A. S. R. Murty and
Bh. V. Ramana Murty , 1982 : Electrical and dynamical characteristics of
summer monsoonc louds. Preprint Volume Regional Conference on Tropical
Meteorology, Tsukuba, Japan, 18-22 October 1982, WMO, Geneva, 249-250.
Mary Selvam, A., A. S. R. Murty, Poonam Sikka and Bh. V. Ramana Murty,
1983b : Some physical and dynamical aspects of warm monsoon clouds and
their modification. Proc. Indian Academy of Sciences (submitted).
Mary Selvam, A., A. S. R. Murty, G.K. Manohar, S. S. Kandalgaonkar and
Bh. V. Ramana Murty, 1984a : A new mechanism for the maintenance of fair
weather electric field and cloud electrification. Preprint Volume VIIth
International Conference on Atmospheric Electricity, 4-8 June 1984, Albany,
New York, Amer. Met. Soc.
Mary Selvam, A., A. S. R. Murty and Bh. V. Ramana Murty, 1984c : Role
of frictional turbulence in the evolution of cloud system. Preprint Volume
9th International Cloud Physics Conference, 21-28 August, 1984, Tallinn,
USSR.
Schmidt, A., 1924 : Zur Frage der elektrischen Vertikalstrome, Z. Geophys.,
1, 281-284.
Tsurutani, B.T., E.J. Smith, R.M. Thorne, R.R. Anderson, D. A. Gumett,
G.K. Parks, C. S. Lin and C. T. Russsell, 1981 : Wave particle interactions
at the magnetopause contributions to the dayside aurora, Geophys. Res.
Letts., 8, 183-186.
Van Zandt, T.E., 1982 : A universal spectrum of buoyancy waves in the
atmosphere, Geophys. Res. Letts., 9, 575-578.
Weinstock, J., 1980 : A theory of gaps in the turbulence spectra of
stably stratified flow, J. Atmos. Sci., 37, 1542-1549.
Weinstock, J., 1981 : Energy dissipation rates of turbulence in the
stable free atmosphere, J. Atmos. Sci., 38, 880-883.