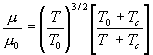§ 1. Основные понятия.

В жидкости и газе можно наблюдать множество красивых явлений: волны, солитоны, когерентные структуры, пену, пузыри, кавитацию, колебательное и вращательное движение, излучение, образование капель и фазовые переходы, фракталы, жидкие пальцы и т.д. Видя эти бесконечные картины хаоса, математики и механики постарались придумать менее хаотичную среду, и вывели её основные уравнения движения. Постепенно была создана механика сплошной среды – раздел механики, посвящённый изучению движения и равновесия газов, жидкостей и деформируемых твёрдых тел. Она подразделяется на гидроаэромеханику, газовую динамику, теорию упругости и теорию пластичности.

Гидроаэромеханика – раздел механики, изучает равновесие и движения жидких и газообразных сред, их взаимодействия между собой и с твердыми телами. Она включает в себя гидродинамику и аэродинамику.

В учебнике "Гидродинамика" Ландау Л.Д. и Лифшица Е.Л. авторы  не придерживаются строгого определения этой науки. Например, излагают теорию одномерного сжимаемого газа. Но если взять книгу Г. Н. Абрамовича, то в нём есть глава "Элементы гидродинамики". Короче говоря, нет чёткой классификации каждой науки и не возможно изложение одной теории без другой.

Полем вектора называют массив компонентов проекций вектора, например, скорости на три оси координат или скалярной величины, например, температуры, плотности, давления, для заданного интервала времени. Газ или жидкость заменяется системой материальных точек нулевого объема или "частиц", для которых и определяются вектора скорости и другие параметры.

Газ считается несжимаемым, если он движется с небольшой скоростью. Число Маха (отношение скорости звука к скорости газа в точке) должно быть M < 0.3. Если газ сжимаем, то нужно учитывать дополнительные члены в уравнениях движения. Жидкость при больших давлениях также становиться сжимаемой.

Когда жидкость или газ имеет конечную плотность в занимаемом ими объеме, используют понятие сплошной среды. Сплошная среда, это физический термин (Аналогично, вместо того, что бы сказать, что мы дышим смесью кислорода, азота и т.д., мы говорим, что дышим воздухом). Вот определение такой среды из [1].

"В отличие от дискретной системы материальных точек, под сплошной средой понимают непрерывное, безграничное или ограниченное множество материальных точек с непрерывным распределением по их множеству вещественных, кинематических, динамических и других физических характеристик, обусловленных разнообразными как "внешними", так и "внутренними" движениями материи, включая сюда и взаимодействие среды с внешними и внутренними полями".

Рассматриваемую область пространства можно поделить на элементарные объёмы, в каждом из которых, параметры среды одинаковы в какой-то момент времени. Принимается, что движущийся объём среды состоит из одних и тех же частиц жидкости. Это возможно благодаря наличию в нём большого числа молекул (1 кубический см воздуха содержит более 2^.10¹⁹ молекул при нормальных условиях). Молекулы могут быть разные, например, у воздуха, но их число в элементарном объёме должно быть очень велико. При уменьшении элементарного объёма концентрация молекул считается постоянной. Если вы считаете, что производная распределения плотности существует и конечна при уменьшении рассматриваемого объёма до нуля, то среду можно считать сплошной. В качестве среды может выступать не только газ или жидкость. Например, сплошной средой можно считать пену, если ее статистические параметры одинаковы в каждой точке или в бесконечно малом объеме, многофазную среду, магнитную жидкость, струю расплавленного металла кумулятивного заряда, твёрдые металлы, бетон, стекло, жидкие кристаллы, землю, пар, аэрогель. Таким образом, введение сплошной среды - это процесс замены реальной среды абстрактной средой. Она подчиняется точно заданной системе дифференциальных уравнений в частных производных с некоторыми начальными и граничными условиями. И не зная коэффициенты, входящие в уравнения невозможно понять, что мы в действительности описываем (жидкость, твёрдое тело или газ). А если рассматривают воздух, то вместо использования плотности каждого компонента воздуха используют некую среду со средней плотностью. Образованием озона в ней пренебрегаем. То есть, происходит не только физическое (с точки зрения введения средней плотности), но и химическое обезличивание среды (не рассматриваются никакие компоненты среды, она считается инертной, как гелий, если не рассматривается горение). Сплошная среда вводиться потому, что невозможно записать систему дифференциальных уравнений для всех молекул и задать для них начальные и граничные условия.

Частным аналогом такой абстракции, например, в математике, является аппроксимация решения системы дифференциальных уравнений полиномом на заданном отрезке.

Приведу примеры нарушения модели сплошной среды. Водяная воронка в ванной. Сначала это сплошная среда, затем по мере уменьшения уровня воды в ванне в центре воронки вода исчезает, образуется вращающаяся воздушная полость. Вода и воздух – это две разные сплошные среды.

В процессе вдува газа в воду среда перестает быть сплошной, когда вода или сжиженный газ кипят, или начинают замерзать, в процессе фазового перехода, при кавитации.

Рассмотрим падающую каплю на плиту. Когда в ней появился первый пузырёк пара, то среда теряет сплошность.

Определим среднюю длину пробега молекул атмосферы в зависимости от высоты. Когда она перестаёт быть намного меньше размеров измеряемого прибора, модель сплошной среды становиться не справедливой. Скорость газа при этом, перестает быть равной нулю на поверхности тела. Наблюдается проскальзывание молекул. Этот факт известен всем, кто проектирует вакуумную технику. Число Кнудсена (отношение длины свободного пробега молекул к наименьшему геометрическому размеру, например, к диаметру трубы, по которой течет газ) должно быть намного меньше единицы, чтобы считать среду сплошной.

В случае если  среда состоит из  льда и пара, число Кнудсена может характеризовать сплошность среды, даже если вам не известно, как меняется температура среды.

Модель не работает в условиях сильного нагрева среды, когда начинается термическая диссоциация и распад молекул на ионы или в случае разряженного газа. В этом случае законы гидромеханики очень грубо или совсем не описывают поведение среды. Для этого переходят к использованию законов статистической физики и использованию методов молекулярной динамики. Среда представляется ансамблем молекул, между которыми действуют силы Ван-дер-Ваальса (притяжения) и валентные силы (отталкивания). Это модель с использованием уравнения Больцмана и бесстолкновительного уравнения Больцмана более точна, чем модель сплошной среды. Этими вопросами немного занимаются и в квантовой химии, в которой изучается свойства групп молекул. Модель не работает при образовании кластеров при конденсации газа или пара, например, когда образуются фуллерены или снежинки. Бессмысленно её использовать при описании процессов внутри живых клеток и тканей, и в тех случаях, когда меняется фрактальная размерность среды.

Уравнения гидромеханики для несжимаемого газа и для жидкости одинаковые. Отличаются только коэффициенты вязкости, теплопроводности. Вязкость воды падает при увеличении температуры, а газа увеличивается. Но сама среда представляется в виде мельчайших шариков, подобно пластилину. Если вязкость равна нулю, то эту среду называют идеальной. Считается, что молекулы вообще не взаимодействуют друг с другом. Вместо пластилина шарики изготовлены из резины. При этом силы Ван-дер-Ваальса, (они не являются векторной величиной) или силы сцепления между шариками равны нулю. Существует состояние изотопов жидкого гелия 4 и 3, когда они находятся в сверхтекучем состоянии. Их вязкость равна нулю. Такую среду, в которой наблюдаются особые квантовые эффекты, так же описывают уравнениями гидромеханики.

Итак, сплошная среда, у которой коэффициенты вязкости, теплопроводности равны нулю, в которой отсутствуют квантовые эффекты, называется идеальной жидкостью или газом. Более точно: идеальный газ - это простейшая модель действительного газа. Считается, что его молекулы  сталкиваются, но не притягиваются друг к другу, и подчиняется распределению Больцмана. Молекулы все время флуктуируют со временем. Рассматривается  3 состояния  идеального газа. При первом, он находиться в равновесии, средняя макроскопическая скорость  газа равна нулю. При втором,  газ находиться в неравновесном состоянии, средняя скорость больше нуля.  В аэрогидродинамике  рассматривается третий случай: газ находиться в неравновесном состоянии, но вязкостью, теплопроводностью пренебрегаем. Уравнения для идеального газа можно применять и к несжимаемым жидкостям, если пренебречь их вязкостью. Поэтому нужно выделять идеальный газ, идеальную жидкость и идеальную среду. Получается, что существует 2 модели идеального газа. Первая модель используется в статистической физике. В аэрогидромеханике  она также используется и модель с коэффициентами вязкости и теплопроводности равными нулю, например при расчете течения в сопле. Во многих случаях используется та модель или их набор, которые удобны пользователю.

 Для течения воды вдали от тела, течения разряженного газа или смеси газов дифференциальные уравнения, описывающие данные течения, будут одинаковыми, но только при определенных условиях и в некоторых областях. Модель идеального газа или жидкости часто  не справедлива  для тонкой области вблизи  поверхности тела, называемой пограничным слоем.  Идеальный газ - это очень простая система и из неё не следует, что газ может конденсироваться в жидкость. Очень интересно смотреть, как идеальный газ вдруг становиться вязким, при выводе формулы вязкости. При большом градиенте скорости формула для  определения коэффициента вязкости опять становиться не справедливой, например, при течении среды в трубке. Течение становиться турбулентным.

Если в качестве уравнения состояния используют уравнение: pV = RT, то идеальный газ называют совершенным.

Необходимо отметить, что точная теория жидкости до сих пор не создана. Если рассматривать небольшую группу молекул воды, то она ведет себя совершенно по-другому, чем вода, как твердое тело. Этот объект называют кластером молекул. Поэтому, в действительности, движение воды – это движение больших кластеров молекул воды, непрерывно меняющих свой размер, из-за взаимодействий между собой и изменения параметров внешней среды. Недавно физики научились получать воду с заданным направлением вращения  протонов в молекулах (они даже думают, что эта "живая" и "мертвая" вода). Свойства каждой воды оказались различные. Существуют изотопы воды, например тяжелая вода. Все эти жидкости в модели сплошной воды будут отличаться только плотностью и коэффициентом сжимаемости. Если  эти параметры одинаковы и их вязкость и теплопроводность одинаковы, то это будет одним и тем же веществом. 

Примером среды, которую можно считать сплошной – это кровь. Но как только она начинает менять свой химический состав, например, свёртываться из-за испарения воды или вас интересует её химический состав, модель сплошной среды использовать нельзя.

Процессы горения также могут быть описаны с использованием модели сплошной среды, когда среда однофазная. Если же среда состоит из пыли и газа, то часто опять переходят к использованию законов статистической физики.

В модели сплошной среды газ или жидкость характеризуется плотностью, 3 компонентами вектора скорости, давлением. Иногда анализируют шесть компонент вектора поверхностных сил, три компоненты объемных или внутренних сил (например, это сила тяжести, сила инерции, действующая на малый объем газа). Вектора поверхностных и объемных сил зависят от вектора скорости и давления. Кроме этого, среду характеризует температура, коэффициент динамической вязкости (функция от температуры) и коэффициент теплопроводности (функция от давления и температуры). Но из уравнения состояния следует, что температура - функция давления и плотности. Поэтому внутренняя энергия не является независимой характеристикой среды. В зависимости от задачи некоторыми параметрами пренебрегают. Например, считают коэффициенты вязкости и теплопроводности постоянными.

При математическом описании считают, что движущая жидкость задается 3 функциями: вектора скорости, давления, плотности. Каждая зависит от 4 параметров: трёх координат и времени, если не учитывать силу тяжести и другие внутренние силы. Часто задают функцию зависимости коэффициента вязкости и теплопроводности от давления и температуры. Всего используется 5 функций. Функция вектора скорости, давления, плотности задаётся для каждой определённой точки пространства, а не для движущейся частицы среды. Число параметров может меняться для каждой среды и задачи. Часто используют вспомогательные функции температуры, внутренней энергии.

Широко используется формула Сатерленда для определения коэффициента динамической вязкости газа:

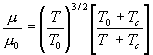Индекс 0 относится к вязкости при некоторой температуре T₀.

Для воздуха = 1,72 10 ^–5 Н ^. с / м² , T_c = 122 K при T₀ = 273 К.

Для воды вязкость можно определить по формуле:

где температура T измеряется по шкале Цельсия.

Можно добавить, что инженеры умеют качать солёную воду, жидкие металлы, плазму магнитным полем специальными насосами. То есть, если солёная вода движется через катушку с постоянным магнитом, которую вы поставите возле прибоя, то по катушке будет течь ток. Его можно увеличить в несколько раз, если вы образуете колебательный контур в системе. Но такими течениями, движением плазмы и магнитной жидкости занимается электродинамика сплошных сред и магнитная гидродинамика.

Если сплошная среда движется со скоростью, близкой к скорости света, что наблюдается при движении газа вблизи чёрных дыр, то необходимо учитывать релятивистские эффекты.

Солитоны или локализованные структуры возникают в газе и жидкости при достаточно сильном воздействии на среду внешних сил, а также в результате нелинейных эффектов взаимодействия элементов среды друг с другом. При слабом воздействии на систему эволюция системы описывается линейными закономерностями. Аналогично, например, закон Гука для пружины выполняется при небольшом её удлинении. Линейные уравнения при решении задачи Коши допускают только волновые пакеты. В основе их распространения лежит принцип суперпозиции, характерный для линейных систем. Но при сильном воздействии на среду или значительных эффектах взаимодействия между элементами среды, принцип суперпозиции нарушается, так как эволюция системы подчиняется нелинейным законам. При этом образуются устойчивые структуры. Изучением их занимается физика солитонов. Эта теория позволила создать оптико-волоконные системы связи и скоростной интернет с доступом 100 Мегабит/с и выше.

Существует состояние среды, называемое турбулентным, когда в среде происходят процессы переноса импульса, энергии, вещества из-за наличия в ней определенного количества солитонов и волн (они могут быть и звуковыми, ударными). Если же этих когерентных структур нет, или они оказывают незначительное влияние на среду, то течение в рассматриваемом объеме называют ламинарным. В среде наблюдается хаотичное изменение мгновенной скорости со временем в каждой точке потока. Коэффициент вязкости, диффузии такой среды намного выше, чем в ламинарном течении. Если вы откроете духи, то благодаря турбулентной диффузии вы быстро почувствуете  их запах в другом углу комнаты.  Осредненные параметры турбулентного течения часто удается предсказывать с достаточной для инженеров точностью. При проведении эксперимента, например, вы видите, что стрелка прибора (манометра давления) все время хаотически колеблется возле некоторого задаваемого вами значения. С математической точки зрения при турбулентном течении наблюдаются хаотически заданные области потенциального и не потенциального векторного поля скорости.

Примером солитона является волна цунами, распространяющаяся со скоростью около 800 км в час на сотни километров с незначительными потерями энергии. Максимальная высота такой волны у берега Аляски была равна более 500 метров! Академик Лаврентьев М.А. предлагал в 60-х годах взорвать водородную бомбу под водой, что бы уничтожить Нью-Йорк. Но когда провели эксперимент, обнаружили сильное затухание волны на суше. Поверхность гриба, образующегося при ядерном взрыве, также может служить примером солитона. Мне кажется, что торнадо, гигантская группа волн (акустических и ударных) и солитонов, служила объектом поклонения и божеством у многих народов.

Рассмотренные некоторые теоретические определения можно свести в таблицы:

Предположения о сплошности среды первым ввел Леонард Эйлер. Эта теория конкурировала с другими теориями. Например, Ньютон считал, что воздух состоит из отдельных, не связанных друг с другом частиц. При обтекании тела они, налетая на тело, отдают ему свой импульс. В этом Ньютон видел причину возникновения подъёмной силы. Предположение о сплошности среды позволяет использовать векторную алгебру, теорию дифференциального и интегрального исчисления. Леонардо да Винчи, который не смог придумать эти теории, считал, что при взмахе крыла плотность воздуха сильно меняется и возникает подъёмная сила.

Кроме гипотезы сплошности делаются предположения о евклидовости пространства, об абсолютности и необратимости времени, о мгновенности передачи тепла с помощью теплопроводности. Обычно считается, что скорость движения среды намного меньше скорости света. Принимаются определенные допущения о свойствах самой среды, об учете теплопроводности, гравитационных или электромагнитных сил.

Для описания движения сплошной среды используют два подхода, связанных с выбором системы координат.

В аэродинамике лопаточных машин наиболее распространен подход Эйлера. Рассматриваются неподвижные точки пространства, и исследуются изменения скорости в этих точках с течением времени. Через них с течением времени проходят различные частицы среды. Координаты неподвижной точки x, y, z и время t называют переменными Эйлера.

При подходе Лагранжа, среда состоит из конечного числа пронумерованных больших частиц.

dx/U(x,y,z,t) = dy/V(x,y,z,t) = dz/W(x,y,z,t) = dt,

Наблюдение ведётся за фиксированной частицей среды определённой массы, которая, подобно надувному шару, меняет свою форму, но не массу. Независимыми переменными является время и номер частицы. Если в качестве переменных Лагранжа выбрать координаты начального положения частицы и время t (хотя время иногда не считают переменной Лагранжа), то в этом случае закон движения для одной любой ее частицы, выражается формулой:

Для получения уравнений (1) необходимо проинтегрировать уравнения:

Например, пусть известна зависимость для скорости в виде:

Проинтегрируем эту систему уравнений:

dy/dt = 0;

dz/dt = 0.

Получим закон движения сплошной среды в переменных Лагранжа для одной частицы:

Постоянные интегрирования заданы из начальных условий.

Существуют формулы перехода от переменных Эйлера к переменным Лагранжа.

Производная Лагранжа равна:

Попробуйте еще ответить на вопрос. Поверхность волны, когда она начинает опрокидываться на берег, это однозначная функция? Мне кажется, что нет. Кипящая вода - это среда, потерявшая сплошность, описывается неоднозначной функцией. Но по определению, обычная функция должна быть однозначной. Поэтому получается, что дифференциальные уравнения гидромеханики не могут вообще описать эти течения, из-за нарушения сплошности среды. Но, тем не менее, приближенно опрокидывание волны удается рассчитать и визуализировать на компьютере. Значит, уравнения гидромеханики иногда точно описывают неоднозначные функции. Поэтому их решение теоретически можно использовать для изображения сложных поверхностей, кривых.

Физики и математики расширили понятие сплошной среды, введя понятие дробной или фрактальной размерности, фрактальной структуры, неравновесной термодинамики, открытой системы. Для меня было сложно представить производную от функции произвольной нецелой размерности. Появилось новое научное направление-синергетика. В металлургии и материаловедении она используются для создания новых материалов (например, фуллеренов и сажи) и оптимизации процессов их получения. Активно используется фрактальный анализ.

Наглядной моделью этих теорий служит позвоночник, адаптирующийся к внешним нагрузкам. Позвонки имеют пористую структуру и содержат жидкость. При перегрузках  между позвонками возникают структуры в межпозвонковой жидкости. Они гасят колебания, (позвоночник работает как демпфер - гаситель колебаний и насос, всасывая и выбрасывая  новую жидкость) и обеспечивают работоспособность при значительных избыточных давлениях. Разность давлений, определяющая скорость течения межпозвонковой жидкости является определяющим параметром в данном процессе. Другим примером самоорганизации диссипативных структур является образование в мозгу упорядоченных структур при восприятии мысли.

Наверное, в будущем появиться неравновесная механика (и гидроаэромеханика) фрактальной среды. Но ответ на вопрос о том, когда нужно использовать фрактальную размерность в уравнениях механики сплошной среды, не совсем ясен. Положение материальной точки считается заданным в пространстве, если заданы её 3 координаты радиус-вектора и вектор скорости в начальный момент времени. Но если фрактальная размерность вводиться в виде функции по пространству и времени, то не ясно, как задавать граничные и начальные условия в этом случае. Понятие материальной точки заменяется некоторой функцией. Поэтому на практике поступают проще, используя аппарат статистической физики, например прямое статистическое моделирование среды, например методом Монте-Карло. Но развивается обобщенная больцмановская кинетическая теория газов, основанная на введении в уравнение Больцмана членов, ответственных за изменение функции распределения на временах порядка времени столкновениях [18]. Расчеты, основанные на этом подходе, иногда дают более точный результат, например, при исследовании распространения звука.

Вопросы к параграфу:

1. Коэффициент вязкости реального газа растет от температуры, а жидкости падает. Как этот экспериментальный факт учитывается в модели идеальной и реальной среды?

   Ответ: В модели реальной среды вводят функции зависимости коэффициентов вязкости от температуры для конкретной среды. Подставляют их в системы дифференциальных уравнений. В модели идеального газа этим формулами пренебрегают, считая вязкость идеального газа и жидкости равной нулю.

2. В турбулентном течении коэффициент вязкости больше или меньше, чем в ламинарном течении?

   Ответ. Больше.

3. Если вы мгновенно заморозите каплю жидкости. Как определить, что она находилась в турбулентном состоянии?

   Ответ. Если посмотреть структуру града, то легко увидеть когерентные структуры. Это не значит, что она находилась в турбулентном состоянии. Она могла несколько раз оттаивать, прежде чем замерзнуть. При замораживании воды, находящей в турбулентном состоянии, цвет льда будет сильно меняется по объему. При быстром замораживании неподвижной среды никаких когерентных структур не наблюдается.

4. Чем волна отличается от солитона?

   Ответ: Волна - изменение какой-либо физической величины. Она способна перемещаться от места возникновения или колебаться внутри ограниченной области. Солитон - это волны в нелинейной среде. Наблюдаются, например, при решении уравнения Кортевега-де Фриса и похожи на частицы. Они локализованы в конечной области, перемещаются без деформации, перенося энергию и импульс, момент импульса. Они способны сохранять свою структуру при соударениях друг с другом и могут объединяться в ансамбли.

5. Дословный перевод японских иероглифов слова турбулентность, означает разбрызгивание вихрей. Приведите пример физического явления, которое наблюдается в реальном турбулентном течении газа или жидкости.

   Ответ: Например, всевозможные колебания, акустические колебания. Морские животные, рыбы слышат инфразвуковые колебания перед штормом или землетрясениями и уплывают на глубину из опасной области.

6. Что такое аэрогель?

   Ответ.

   Это новое состояние вещества (например, кремния), занимающее промежуточное состояние между твёрдым телом и газом. Используется для улавливания частиц пыли комет на космических аппаратах. Плотность этого вещества намного меньше плотности всех твердых тел.

7. В 1827 г. ботаник Броун наблюдал беспорядочное движение пыльцы (размер частиц 1 мкм), взвешенных в воде, происходящее под действием ударов молекул воды. В метрологии это движение рассматривают как основной фактор, ограничивающий точность чувствительности измерительных приборов. Предел точности измерений оказывается достигнутым, когда броуновское смещение подвижных частей измерительного прибора по порядку величины совпадает со смещением, вызванным измеряемым эффектом.

   Вопрос. При турбулентном течении так же наблюдается беспорядочное движение измерительной стрелки, возле измеряемого значения, однако предел точности измерений не оказывается достигнутым. Почему?

   Ответ. Из-за разницы масштабов. Так как с помощью оптических методов измерений, например лазерно-доплеровской анемометрии, удается измерять мгновенные поля скоростей турбулентного течения. Его размеры на несколько порядков превышают размеры пыльцы.

8. Когда воздух, смесь более чем 10 газов, можно считать идеальным газом?

   Ответ. Отклонение воздуха от свойств идеального газа характеризует коэффициент сжимаемости, который при 0 градуса Цельсия равен 1,0006. Поэтому при не больших скоростях движения или когда его можно считать несжимаемым, удовлетворяющим модели идеального газа вдали от поверхности тела. Число Кнудсена должно быть намного меньше единицы. То есть должна быть справедлива модель сплошной среды. Температура воздуха должна быть не ниже температуры замерзания каждого компонента и не выше температуры диссоциации.

9. Диссипативной средой называют физическую систему, в которой энергия одних движений или полей обычно упорядоченных необратимым образом переходит в энергию других движений или полей, в конечном счете, в теплоту. Если диссипация энергии происходит в замкнутой системе (например, в термосе), то энтропия системы возрастает. В открытых системах диссипация энергии, обусловленная уносом энергии из системы, например в виде звука, волн, может приводить к уменьшению энтропии рассматриваемой системы при увеличении полной энтропии системы и окружающей среды. Можно наблюдать диссипативные структуры (ячейки Бенара, перистые облака, неоднородные распределения концентрации в химических реакторах), спонтанное развитие структур в живом организме, окраску поверхности тел животных. Столкновения молекул в газах приводят к необратимым процессам внутреннего трения и теплопроводности.

   Вопрос. Когда, глядя на систему дифференциальных уравнений, описывающих среду, мы можем предполагать, что она является диссипативной?

   Ответ. Когда есть параметры диссипативной среды, коэффициент сдвиговой, объемной, динамической и турбулентной вязкости, коэффициент теплопроводности. Когда силы сопротивления не равны нулю.

10. К газовой динамике часто относят акустику, динамическую метеорологию, электро и магнитогазодинамику, динамику разряженных газов, динамику плазмы. Какие два подхода используют при описании сплошной среды?

    Ответ. Статистическое описание поведения частиц, составляющих среду (в теории плазмы и разряженных газов) и подход на основе сплошной среды, с использованием средних по малому объёму значений массы, импульса, энергии.

11. Какой синоним словосочетанию распространение слабых возмущений можно использовать?

Рекомендуемая литература к параграфу: