Creador: Marcelo Torres Vea las estadísticas de esta página aquí

Empezando por...

No me gustan los sitios que explican y que contienen solo texto y referencias a los creadores de las pagina, y sus proyectos. Por esto intentare en esta pagina ser un poco mas practico, y de este modo quedar contento con migo mismo.

Yo pretendo mostrar ejemplos clásicos y básicos de redes neuronas, además, entregare un poco de código fuente a modo de ejemplo, tal vez algunos programas ejecutables y consejos de cómo entrenar alguna que otra red neuronal.

Lo básico en redes neuronales.

Las redes neuronales básicas están basadas en el principio de repetición para aprender (Hebb),como niño chico. Su estructura física esta basada en lo que se piensa que son las neuronas. Aquí debe haber una figura.



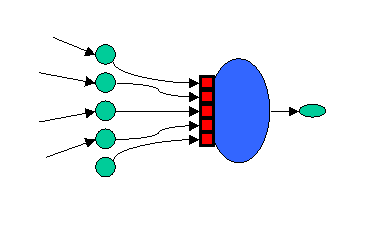
Estas neuronas reciben una serie de entradas X, las ponderan por factores W y de forma lineal (mediante una función lineal) entregan un resultado.

Función F(X·W)=Y

	X=( x1,x2,...,xn,1)
	W=(w1,w2,...,wn,wn+1)t
	Y'= F( w1*x1+w2*x2+...+wn·xn+wn+1·1)

El truco esta en conseguir que el algoritmo de aprendizaje de la red neuronal establezca relaciones entre una serie de vectores X para una serie de vectores Y, y esperar que estos vectores sean lo suficientemente representativos como para extender esta relación a otros casos intermedios.

Para no aproblemarnos la función F será la función de identidad F(Z)=Z.



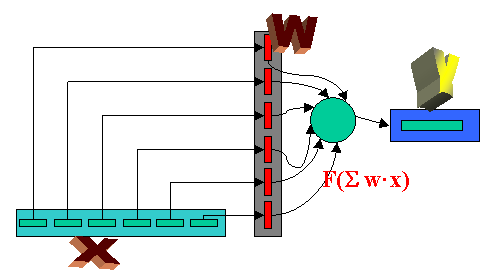
¿Que son estos vectores?

Son representaciones de lo que queremos relacionar con esta red, caso típico una imagen. Lo importante es que cualquiera que halla sido su anterior conformación ahora está representado por un vector que contiene unos (1), ceros (0) o menos 1 (-1).



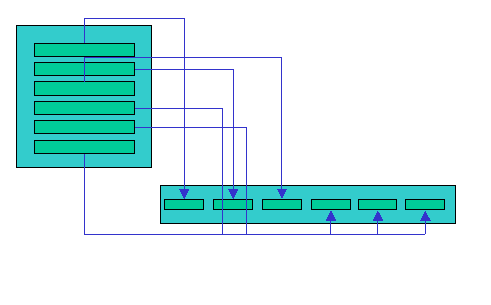
El algoritmo de aprendizaje se aplica repetidas veces para un conjunto conocido de vectores X e Y, la idea es que la salida calculada Y' sea lo menos diferente posible al vector propuesto.

El error es simple Y' - Y,

El error para el conjunto total de vectores es de 1/2å ( Y'²- Y²)

Atención los factores w_i se denominan pesos, y es obvio que W es un vector de pesos.

En esta parte siempre se utilizan una boragine de sub y super índices pero yo no los usare.

Cualquiera que programe un poco sabe que:

I= I+1

No es ( en programación) una contradicción de lógica, es una actualización o reemplazo del valor almacenado en I por el valor de I+1.

Ya aclarado esto, la forma de adecuar los pesos es la siguiente:

W=W+ h X·(Y'-Y).

¡Simple!

Bueno en rigor falta la función derivada de F pero como esta es id(identidad) esta función es 1

W = W + h X·(Y'-Y)·F'(Y) [no usar]

Donde h es un valor entre 0 y 1 que representa la violencia con que irrumpirán los cambios en la red, si la red es pequeña y las relaciones son pocas este valor será 1, mientras mas entradas h deberá ser menor.

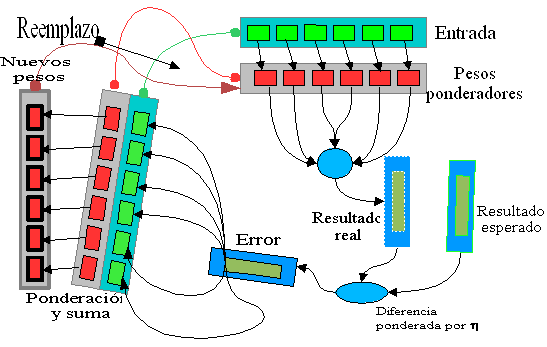
 Si el parametro es muy grande es posible que la red jamas converja lo suficiente como para concretar un entrenamiento efectivo. Si en cambio es muy pequeño nunca llegara a producir resultados lo suficiente cercanos a lo esperado.

Tambien se debe recordar que al entrenar la red de deben usar ejemplos distribuidos de modo hómogeneo dentro del espacio de posibles entradas-soluciones, y no es suficiente, en general si se puede ordenar las entradas de algún modo, no lo haga, coloquelas en desorden de otro modo olvidara los ejemplos que corresponan con el inicio de la lista

Encuentro necesario el mensionar que este desorden se aplica con las salidas, me explico, la entrada y la salida corresponden a un par, de modo que si se modifica el orden en que las entradas se aplican, este cambio se aplica del mismo modo a las salidas.

Bajo construcción

Visitantes :

This page hosted by
Get your own Free Home Page