Formule di Cardano

A) Equazioni di 3° grado.

Consideriamo l’equazione di terzo grado:

Dividiamo primo e secondo membro per a e quindi possiamo supporre a=1. Troviamo allora un’equazione del tipo:

Facciamo la sostituzione:

otteniamo allora la nuova equazione:

equivalente a:

che a sua volta è equivalente ad un’equazione del tipo:

Dunque l’equazione di partenza si è trasformata in un’equazione del tipo:

Consideriamo ora l’identità:

Se si trovano u e v tali che:

allora u+v è una soluzione dell’equazione (*).

Dal sistema (**) segue:

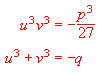Quindi di e si conoscono somma e prodotto e quindi e sono le soluzioni dell’equazione:

Dato il ruolo simmetrico giocato da u e v (siccome ci interessa trovare la soluzione dell’equazione (*)) possiamo supporre che:

da cui:

(sono 3 redici complesse) e

quindi: u+v è la soluzione cercata.

B) Equazioni di 4° grado

Come nel caso precedente, si può supporre che l’equazione sia del tipo:

Se abbiamo un’equazione del tipo:

allora poniamo

ottenendo l’equazione:

Svolgendo le potenze si ottiene:

Consideriamo ora l’identità:

Se riusciamo a trovare che soddisfano il sistema:

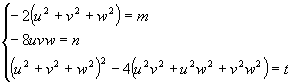
allora u+v+w è una soluzione dell’equazione (*). Dei numeri e si conoscono la somma , il prodotto e l’espressione:

Si tratta quindi degli zeri del polinomio:

Questa è un’equazione di III grado della forma di quella precedente. Troviamo, per quanto detto prima, e quindi la radice cercata u+v+w.

Formule per il calcolo delle soluzioni di equazioni di grado maggiore o uguale a 5 non ne esistono e non possono esisterne. Questo teorema è stato dimostrato da Galois.