LCR in a nut shell
This page assumes that you have some background about the LCR circuit and you are reading it for refresh or for further details.
The diameter of the wire doubles in every 6 AWG.
Example:
50 AWG = 1 mil
44 AWG = 2 mil
38 AWG = 4 mil
32 AWG = 8 mil
26 AWG = 16 mil and so on…
Inductor
1. Straight wire Inductance
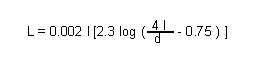
Where:
L: Inductance in micro Henry
I: Length of wire in cm
d: Diameter of wire in cm
2. Single layer air core Inductor
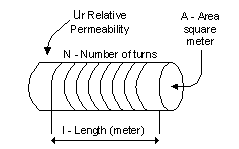
The self Inductance of the above coil is:
L: Inductance in Henry
N: Number of turns
A: Area of coil in square meter
I: Length of coil in meter
Uo: Free space permeability in henry per meter
Ur: Relative permeability of the coil
For optimum coil Q factor the following formula is used to calculate the inductance:
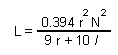
Where:
L: The inductance in micro henry
l : Coil length in cm
r: Coil radius in cm
For the above formula to be accurate the following condition must be met:
l > 0.67 r
and for optimum Q factor the following condition must be met:
l = 2 r
Therefore a wire with the right
AWG must be selected to fit the calculated number of turns.
3. Toroidal Inductance
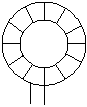
Where:
L: Inductance in micro Henry
N: Number of turns
Ui: Initial permiability
Ac: Cross sectional are of toroid in cm square
Ie: effective length of core in cm.
If the current flows inside the toroid a magnetic field is generated. The magnetic flux (phi) are lines of forces that don't intersect, repel each others, and form closed loops. Flux is measured in Weber (Wb). If a conductor cuts a flux of 1 Weber in one second then the voltage induced in the conductor is one volt. Flux Density (B field) is an indicator of the magnetic field strength and is measured in Weber per meter (Wb / meter or Tesla).
B = (phi / A)
Where:
B: Flux density in Tesla
Phi: Magnetic flux in Weber (Wb)
A: Area intercepting the field (in meter square)
4. Loop Inductance
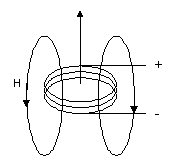
Where:
L: Inductance in Henry
N: Number of turns
Uo: Magnetic field constant (1.257 x 10e-6 Volt Second/Ampere meter)
R: Radius of loop in meter
d: Diameter of wire used in meter
5. Square Loop Inductance
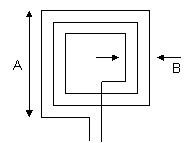
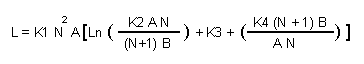Where:
L: Inductance in micro henry
A: length of the square side in cm
B: Width of the coil in cm
N: Number of turns in close winding
K1: 0.006
K2: 1.4142
K3: 0.3794
K4: 0.3333
Time Constant
The voltage across the capacitor is:
and the voltage across the resistor is:
The time constant T = RC. The capacitor voltage at 1 time constant is 0.632 of the final value (maximum voltage), and almost maximum supply voltage at 5 times constant.
The time constant for LR circuit is L/R. In LR circuit the final value (Max) is the current and not voltage as compared to RC circuit.
L Circuit - Lead circuit
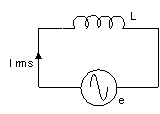
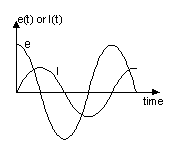
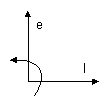
Voltage e(t) across inductor leads the current I(t) by 90 degrees.
eLi as in "eLi the iCe man."
V (coil) = - L (di / dt)
Xl = w L
W = 2 pi f
C Circuit - Lag circuit
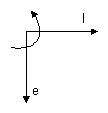
Voltage e(t) across capacitor lags the current I(t) by 90 degrees.
iCe as in "eLi the iCe man."
I (capacitor) = C (de / dt)
Xc = (1 / wC)
W = 2 pi f
Lead Lag Networks
|
|
|
The current in each component is same but voltages are different.
If R = 0 then Xc = Xl at resonance; fr = 1 / (2 pi sqrt (LC) )
When Xc = Xl the current will be Max. If R is > 0 the current Irms starts to drop as R increases.
When Xc = Xl at certain resonance frequency fr the current only depends on R.
Total impedance is:
The resultant Impedance is the vector addition of capacitate, inductive, and resistive elements. If the result is capacitate (Xc) then the network is
Lag network: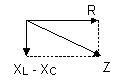
If the result is inductive (X
L) the network is then Lead network: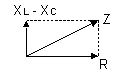
to Index
Firas Faham, Design Engineer
