


V.A.Kaimanovich (1), E.M.Krupitski (2) and A.V.Spirov (3)1) Department of Mathematics and Statistics, University of Edinburgh, Edinburgh EH9 3JZ, Great Britain 2) Research Laboratory of the Regional Narcological Center, St.Petersburg, Russia 3) I.M. Sechenov Institute of Evolutionary Physiology & Biochemistry St.Petersburg, Russia
For a numerical realization of the above model we consider the cell surface to be the sphere with a geodesic grid on it. The diffusion equations (1) and (2) are replaced with the corresponding difference equations in a standard way.
The computational scheme corresponding to this model is the following
one: for a given set of values of 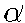 the system of difference equations obtained from the differential
equations (1) and (2) is run until a stationary solution is achieved.
Then the initial set of values of
the system of difference equations obtained from the differential
equations (1) and (2) is run until a stationary solution is achieved.
Then the initial set of values of 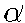 is replaced with a new set of values obtained by formula (3),
where V are stationary values of the
potential, and so on.
is replaced with a new set of values obtained by formula (3),
where V are stationary values of the
potential, and so on.
Equations (1), (2) in our model are realised on a sphere (zygote
surface). The sphere is divided by 29 parallels and 30 meridians
in to 900 surface elements. Difference in their sizes is taken
into account by using for numerical integration of this system
a difference scheme with weights for diffusion-type equations
with variable coeffcients. Parameter L equals
5. According to Fromherz, the values of time steps are chosen
as 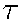 = 0.1 and
= 0.1 and 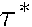 =
0.0001. The boundary conditions on the "animal" and
"vegetal" poles of the model are N
= V = 0. Initial values of parameters
are chosen as
=
0.0001. The boundary conditions on the "animal" and
"vegetal" poles of the model are N
= V = 0. Initial values of parameters
are chosen as 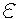 = 8 ;
= 8 ; 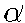 = 1.1, so that the zero solution of the system N
= 0 ; V = 0 is unstable. The initial
perturbation is introduced in the frst circle of animal elements
by putting N(1,i)
= 0.5. The values of parameters in equation (3) are
= 1.1, so that the zero solution of the system N
= 0 ; V = 0 is unstable. The initial
perturbation is introduced in the frst circle of animal elements
by putting N(1,i)
= 0.5. The values of parameters in equation (3) are 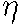 = 0.3 and Vcr =
2 (the qualitative behaviour of the model did not show any significant
dependence on the value of Vcr
).
= 0.3 and Vcr =
2 (the qualitative behaviour of the model did not show any significant
dependence on the value of Vcr
).
After the frst run (300 steps) of numerical integration an animal-vegetal
gradient of potential V and channel
density N stabilizes in the form of
a semiwave (Fig. 1a). After changing the parameter 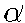 according to equation (3) (which leads to a loss of stability
of the pattern), the next run is carried out. By the step 1000
a new pattern stabilizes, which corresponds to a broadening of
the animal zone of highly ordered orientation of MT bundles (Fig.
1b).
according to equation (3) (which leads to a loss of stability
of the pattern), the next run is carried out. By the step 1000
a new pattern stabilizes, which corresponds to a broadening of
the animal zone of highly ordered orientation of MT bundles (Fig.
1b).
a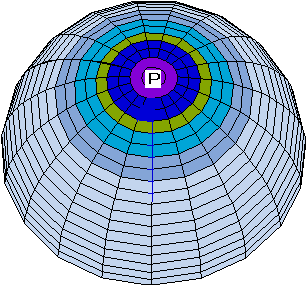 b
b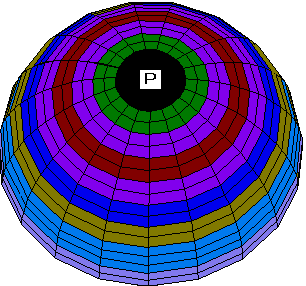
c d
d
Fig 1. a, b. Stages of the spreading of the radial electrical polarization wave from the pole of the modeled zygote envelope to equator areas with symmetric initial data.
c, d. Schematic pictures of dynamics of the wave of "cortical" microtubules vectorization in the zygote envelope conditioned by the wave of electric polarization of the envelope.
After the second change of 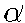 the
system again becomes unstable. In the third run after 400 steps
a new pattern of V stabilizes, corresponding
to a further spreading of the wave of MT vectorization from the
animal pole to the equator. The wave of electric potential V
reaches the equator area and dies down (as well as the induced
wave of the vectorization of cortical MT bundles). This picture
remains the same at further runs. Thus, this result simulates
the spreading of the wave of cortical MT vectorization from the
site of initial perturbation. This phenomenon could be signifcant
for understanding of such processes as the waves of actin polymerization
in the oocyte cortex induced by fertilization and high ordering
of MT bundles in the zygote cortex.
the
system again becomes unstable. In the third run after 400 steps
a new pattern of V stabilizes, corresponding
to a further spreading of the wave of MT vectorization from the
animal pole to the equator. The wave of electric potential V
reaches the equator area and dies down (as well as the induced
wave of the vectorization of cortical MT bundles). This picture
remains the same at further runs. Thus, this result simulates
the spreading of the wave of cortical MT vectorization from the
site of initial perturbation. This phenomenon could be signifcant
for understanding of such processes as the waves of actin polymerization
in the oocyte cortex induced by fertilization and high ordering
of MT bundles in the zygote cortex.
Another set of boundary conditions gives rise to a series of patterns similar to some processes of ooplasmic segregation in ascidian zygote. Consider the zero boundary conditions along the zero meridian. Then for the same values of parameters as in the previous case the geometry of boundary conditions leads to a pronounced asymmetry of the V and N patterns (Fig. 2a, 2b). Both waves still spread from the animal pole to the equator, but the wave of ion channels is excentric with respect to the wave of MT vectorization.
a b
b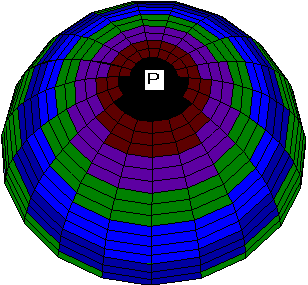
Fig. 2. a, b. Stages of the excentrical spreading
of the radial electrical polarization wave from the pole of the
zygote envelope to equator areas at other boundary conditions
than on Fig.1.
The pattern evolution illustrated by Fig. 2 is stable with respect
to changing parameters within a certain range. When the value
of 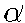 exceeds 1.3, the picture changes
drastically. Instead of propagation of wave fronts, initial gradients
with maxima on the animal pole sharply transform in to gradients
with maxima on the vegetal pole. As a result, cortical MT are
first vectorized on the animal pole, and then on the vegetal pole,
whereas there is no vectorization on the equator. This phenomenon
of potential growth and vectorization of MT bundles first on the
animal pole, and then on the vegetal pole could serve for a highly
directed transport of macromolecules first to one pole, and then
to the other one.
exceeds 1.3, the picture changes
drastically. Instead of propagation of wave fronts, initial gradients
with maxima on the animal pole sharply transform in to gradients
with maxima on the vegetal pole. As a result, cortical MT are
first vectorized on the animal pole, and then on the vegetal pole,
whereas there is no vectorization on the equator. This phenomenon
of potential growth and vectorization of MT bundles first on the
animal pole, and then on the vegetal pole could serve for a highly
directed transport of macromolecules first to one pole, and then
to the other one.