| Acerca de... |
| Geocities |
| Home |
Potencia disipada en los elementos resistivosSi quisiéramos averiguar las potencias disipadas en los elementos, tendríamos que aplicar simplemente la siguiente fórmula:Vemos pues, que los únicos elementos que disipan potencia (tanto en el caso mecánico como eléctrico) son los elementos de tipo resistivo. Hay que hacer notar que en la fórmula anterior (y en lo que sigue) me refiero a potencia media, o activa. En el caso eléctrico, la potencia disipada en una resistencia será: En el caso mecánico, mediante analogía de impedancia, sustituimos resistencia eléctrica por resistencia mecánica, y corriente por velocidad, de forma que obtenemos la potencia disipada en una resistencia mecánica:
Si ahora hacemos el análogo de movilidad, sustituiremos resistencia eléctrica por responsabilidad mecánica (la inversa de la resistencia mecánica), y corriente por fuerza, de forma que obtenemos de igual forma que antes la potencia disipada en una resistencia mecánica: 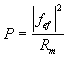 Si igualamos los términos de la derecha de las dos expresiones anteriores, vemos que despejando Rm nos queda:
quedando demostrado que el proceso es correcto.
Energía almacenada en los elementos reactivosLos elementos reactivos no disipan potencia, pero almacenan una energía que se disipará en forma de potencia en los elementos resistivos. La potencia disipada en los elementos reactivos (bobina y condensador) es nula puesto que existe un desfase de pi/2 entre la tensión instantánea y la corriente instantánea del componente. Eléctricamente sabemos que en el caso de una bobina se cumple: 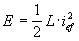 Por lo que haciendo el análogo mecánico de impedancia, sabemos que en una masa mecánica la energía viene dada por: 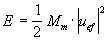 Y haciendo el análogo mecánico de movilidad obtenemos que la energía en un resorte viene dada por:
Otra forma de obtener la energía del resorte y de la masa es obteniéndola a partir de la analogía (de movilidad e impedancia) del condensador. De igual forma a como hemos hecho con la bobina, sabemos que la energía almacenada en un condensador es: 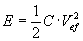
Por lo que haciendo el análogo mecánico de impedancia,
sabemos que en un resorte la energía viene dada por:
Y haciendo el análogo mecánico de movilidad obtenemos que la energía en la masa mecánica viene dada por: 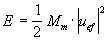
Método práctico de cambio de analogía (Movilidad a Impedancia)Como hemos visto, lo normal es crear el análogo de movilidad de el circuito mecánico. Si queremos obtener el análogo de impedancia, podemos obtenerlo a partir de el circuito eléctrico de movilidad a través de la propiedad de dualidad.En la práctica, existe un método gráfico que permite de forma simple obtener el circuito de movilidad a partir del de impedancia. Es el llamado "método del punto". Sea el siguiente circuito mecánico de movilidad generado a partir de un sistema mecánico determinado: 
El procedimiento es el siguiente:
|
| Anatomía y Fisiología del Oído | El Modelo | Links |
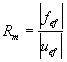 , lo que es cierto, ya que,
, lo que es cierto, ya que, 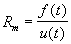
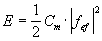 o lo que es lo mismo
o lo que es lo mismo