| H O M E -------- S O F T W A R E -------- C O C O M O -------- METRICS AND MODELS |
Software cost estimation is the process of predicting the amount of effort required to build a software system. Models provide one or more mathematical algorithms that compute cost as a function of a number of variables. Size is a primary cost factor in most models and can be measuring using lines of code or function points. Models used to estimate cost can be categorized as either cost models or constraint models. COCOMO is an example of a cost model and SLIM is an example of a constraint model. Although criteria for evaluating a model have been suggested, there are some fundamental problems with existing models. Many models are available as automated tools.
Software cost estimation is the process of predicting the amount of effort required to build a software system. Cost estimates are needed throughout the software lifecycle. Preliminary estimates are required to determine the feasibility of a project. Detailed estimates are needed to assist with project planning. The actual effort for individual tasks is compared with estimated and planned values, enabling project managers to reallocate resources when necessary.
Analysis of historical project data indicates that cost trends can be correlated with certain measurable parameters. This observation has resulted in a wide range of models that can be used to assess, predict, and control software costs on a real-time basis. Models provide one or more mathematical algorithms that compute cost as a function of a number of variables.
SizeSize is a primary cost factor in most models. There are two common ways to measure software size: lines of code and function points.
Lines of CodeThe most commonly used measure of source code program length is the number of lines of code (LOC) (Fenton, 1997). The abbreviation NCLOC is used to represent a non-commented source line of code. NCLOC is also sometimes referred to as effective lines of code (ELOC). NCLOC is therefore a measure of the uncommented length.
The commented length is also a valid measure, depending on whether or not line documentation is considered to be a part of programming effort. The abbreviation CLOC is used to represent a commented source line of code (Fenton, 1997).
By measuring NCLOC and CLOC separately we can define:
total length (LOC) = NCLOC + CLOC
KLOC is used to denote thousands of lines of code.
Function PointsFunction points (FP) measure size in terms of the amount of functionality in a system. Function points are computed by first calculating an unadjusted function point count (UFC). Counts are made for the following categories (Fenton, 1997):
- External inputs – those items provided by the user that describe distinct application-oriented data (such as file names and menu selections)
- External outputs – those items provided to the user that generate distinct application-oriented data (such as reports and messages, rather than the individual components of these)
- External inquiries – interactive inputs requiring a response
- External files – machine-readable interfaces to other systems
- Internal files – logical master files in the system
Once this data has been collected, a complexity rating is associated with each count according to Table 1.
Table 1. Function point complexity weights.
| Weighting Factor | |||
| Item | Simple | Average | Complex |
| External inputs | 3 | 4 | 6 |
| External outputs | 4 | 5 | 7 |
| External inquiries | 3 | 4 | 6 |
| External files | 7 | 10 | 15 |
| Internal files | 5 | 7 | 10 |
Each count is multiplied by its corresponding complexity weight and the results are summed to provide the UFC. The adjusted function point count (FP) is calculated by multiplying the UFC by a technical complexity factor (TCF). Components of the TCF are listed in Table 2.
Table 2. Components of the technical complexity factor.
| F1 | Reliable back-up and recovery | F2 | Data communications |
| F3 | Distributed functions | F4 | Performance |
| F5 | Heavily used configuration | F6 | Online data entry |
| F7 | Operational ease | F8 | Online update |
| F9 | Complex interface | F10 | Complex processing |
| F11 | Reusability | F12 | Installation ease |
| F13 | Multiple sites | F14 | Facilitate change |
Each component is rated from 0 to 5, where 0 means the component has no influence on the system and 5 means the component is essential (Pressman, 1997). The TCF can then be calculated as:
TCF = 0.65 + 0.01(SUM(Fi))
The factor varies from 0.65 (if each Fi is set to 0) to 1.35 (if each Fi is set to 5) (Fenton, 1997). The final function point calculation is:
FP = UFC x TCF
Types of ModelsThere are two types of models that have been used to estimate cost: cost models and constraint models (Fenton, 1997).
Cost ModelsCost models provide direct estimates of effort. These models typically have a primary cost factor such as size and a number of secondary adjustment factors or cost drivers. Cost drivers are characteristics of the project, process, products, or resources that influence effort. Cost drivers are used to adjust the preliminary estimate provided by the primary cost factor (Fenton, 1997).
A typical cost model is derived using regression analysis on data collected from past software projects. Effort is plotted against the primary cost factor for a series of projects. The line of best fit is then calculated among the data points. If the primary cost factor were a perfect predictor of effort, then every point on the graph would lie on the line of best fit. In reality however, there is usually a significant residual error. It is therefore necessary to identify the factors that cause variation between predicted and actual effort. These parameters are added to the model as cost drivers (Fenton, 1997).
The overall structure of regression-based models takes the form:
E = A + B x S^C
where A, B, and C are empirically derived constants, E is effort in person months, and S is the primary input (typically either LOC or FP) (Pressman, 1997).
The following are some examples of cost models using LOC as a primary input (Pressman, 1997):
| E = 5.2 x (KLOC)^0.91 | Walston-Felix Model |
| E = 5.5 + 0.73 x (KLOC)^1.16 | Bailey-Basili Model |
| E = 3.2 x (KLOC)^1.05 | COCOMO Basic Model |
| E = 5.288 x (KLOC)^1.047 | Doty Model for KLOC > 9 |
Cost models using FP as a primary input include (Pressman, 1997):
| E = -12.39 + 0.0545 FP | Albrecht and Gaffney Model |
| E = 60.62 x 7.728 x 10^-8 FP^3 | Kemerer Model |
| E = 585.7 + 15.12 FP | Matson, Barnett, and Mellichamp Model |
Constraint models demonstrate the relationship over time between two or more parameters of effort, duration, or staffing level (Fenton, 1997). The RCA PRICE S model and Putnam’s SLIM model are two examples of constraint models.
COCOMOBoehm derived a cost model called COCOMO (Constructive Cost Model) using data from a large set of projects at TRW, a consulting firm based in California (Fenton, 1997). COCOMO is a relatively straightforward model based on inputs relating to the size of the system and a number of cost drivers that affect productivity. The original COCOMO model was first published in 1981 (Boehm, 1981). Boehm and his colleagues have since defined an updated COCOMO, called COCOMO II, that accounts for recent changes in software engineering technology (Fenton, 1997).
Original COCOMOThe original COCOMO is a collection of three models: a Basic model that is applied early in the project, an Intermediate model that is applied after requirements are specified, and an Advanced model that is applied after design is complete (Fenton, 1997). All three models take the form:
E = aS^b x EAF
where E is effort in person months, S is size measured in thousands of lines of code (KLOC), and EAF is an effort adjustment factor (equal to 1 in the Basic model) (Fenton, 1997). The factors a and b depend on the development mode. Boehm has defined three development modes:
Basic
- Organic mode – relatively simple projects in which small teams work to a set of informal requirements (ie. thermal transfer program developed for a heat transfer group).
- Semi-detached mode – an intermediate project in which mixed teams must work to a set of rigid and less than rigid requirements (ie. a transaction processing system with fixed requirements for terminal hardware and software).
- Embedded mode – a project that must operate within a tight set of constraints (ie. flight control software for aircraft).
The Basic COCOMO model computes effort as a function of program size (Pressman, 1997). The Basic COCOMO equation is:
E = aKLOC^b
The factors a and b for the Basic COCOMO model are shown in Table 3 (Boehm, 1981).
Table 3. Effort for three modes of Basic COCOMO.
| Mode | a | b |
| Organic | 2.4 | 1.05 |
| Semi-detached | 3.0 | 1.12 |
| Embedded | 3.6 | 1.20 |
The Intermediate COCOMO model computes effort as a function of program size and a set of cost drivers (Pressman, 1997). The Intermediate COCOMO equation is:
E = aKLOC^b x EAF
The factors a and b for the Intermediate COCOMO model are shown in Table 4 (Boehm, 1981).
Table 4. Effort parameters for three modes of Intermediate COCOMO.
| Mode | a | b |
| Organic | 3.2 | 1.05 |
| Semi-detached | 3.0 | 1.12 |
| Embedded | 2.8 | 1.20 |
The effort adjustment factor (EAF) is calculated using 15 cost drivers. The cost drivers are grouped into four categories: product, computer, personnel, and project. Each cost driver is rated on a six-point ordinal scale ranging from low to high importance. Based on the rating, an effort multiplier is determined using Table 5 (Boehm, 1981). The product of all effort multipliers is the EAF.
Table 5. Software Development Effort Multipliers.
| Cost Driver | Description | Rating | |||||
| Very Low | Low | Nominal | High | Very High | Extra High | ||
| Product | |||||||
| RELY | Required software reliability | 0.75 | 0.88 | 1.00 | 1.15 | 1.40 | - |
| DATA | Database size | - | 0.94 | 1.00 | 1.08 | 1.16 | - |
| CPLX | Product complexity | 0.70 | 0.85 | 1.00 | 1.15 | 1.30 | 1.65 |
| Computer | |||||||
| TIME | Execution time constraint | - | - | 1.00 | 1.11 | 1.30 | 1.66 |
| STOR | Main storage constraint | - | - | 1.00 | 1.06 | 1.21 | 1.56 |
| VIRT | Virtual machine volatility | - | 0.87 | 1.00 | 1.15 | 1.30 | - |
| TURN | Computer turnaround time | - | 0.87 | 1.00 | 1.07 | 1.15 | - |
| Personnel | |||||||
| ACAP | Analyst capability | 1.46 | 1.19 | 1.00 | 0.86 | 0.71 | - |
| AEXP | Applications experience | 1.29 | 1.13 | 1.00 | 0.91 | 0.82 | - |
| PCAP | Programmer capability | 1.42 | 1.17 | 1.00 | 0.86 | 0.70 | - |
| VEXP | Virtual machine experience | 1.21 | 1.10 | 1.00 | 0.90 | - | - |
| LEXP | Language experience | 1.14 | 1.07 | 1.00 | 0.95 | - | - |
| Project | |||||||
| MODP | Modern programming practices | 1.24 | 1.10 | 1.00 | 0.91 | 0.82 | - |
| TOOL | Software Tools | 1.24 | 1.10 | 1.00 | 0.91 | 0.83 | - |
| SCED | Development Schedule | 1.23 | 1.08 | 1.00 | 1.04 | 1.10 | - |
The Advanced COCOMO model computes effort as a function of program size and a set of cost drivers weighted according to each phase of the software lifecycle. The Advanced model applies the Intermediate model at the component level, and then a phase-based approach is used to consolidate the estimate (Fenton, 1997).
The 4 phases used in the detailed COCOMO model are: requirements planning and product design (RPD), detailed design (DD), code and unit test (CUT), and integration and test (IT). Each cost driver is broken down by phase as in the example shown in Table 6 (Boehm, 1981).
Table 6. Analyst capability effort multiplier for Detailed COCOMO.
| Cost Driver | Rating | RPD | DD | CUT | IT |
| ACAP | Very Low | 1.80 | 1.35 | 1.35 | 1.50 |
| Low | 0.85 | 0.85 | 0.85 | 1.20 | |
| Nominal | 1.00 | 1.00 | 1.00 | 1.00 | |
| High | 0.75 | 0.90 | 0.90 | 0.85 | |
| Very High | 0.55 | 0.75 | 0.75 | 0.70 |
Estimates made for each module are combined into subsystems and eventually an overall project estimate. Using the detailed cost drivers, an estimate is determined for each phase of the lifecycle.
COCOMO IIWhereas COCOMO is reasonably well matched to custom, build-to-specification software projects, COCOMO II is useful for a much wider collection of techniques and technologies. COCOMO II provides up-to-date support for business software, object-oriented software, software created via spiral or evolutionary development models, and software developed using commercial-off-the-shelf application composition utilities (Boehm et al, 1997). COCOMO II includes the Application Composition model (for early prototyping efforts) and the more detailed Early Design and Post-Architecture models (for subsequent portions of the lifecycle).
The Application Composition ModelThe Application Composition model is used in prototyping to resolve potential high-risk issues such as user interfaces, software/system interaction, performance, or technology maturity. Object points are used for sizing rather than the traditional LOC metric.
An initial size measure is determined by counting the number of screens, reports, and third-generation components that will be used in the application. Each object is classified as simple, medium, or difficult using the guidelines shown in Tables 7 and 8 (Fenton, 1997).
Table 7. Object point complexity levels for screens.
| Number and source of data tables | |||
| Number of views contained | Total <4 | Total <8 | Total 8+ |
| <3 | simple | simple | medium |
| 3-7 | simple | medium | difficult |
| 8+ | medium | difficult | difficult |
Table 8. Object point complexity levels for reports.
| Number and source of data tables | |||
| Number of views contained | Total <4 | Total <8 | Total 8+ |
| <3 | simple | simple | medium |
| 3-7 | simple | medium | difficult |
| 8+ | medium | difficult | difficult |
The number in each cell is then weighted according to Table 9. The weights represent the relative effort required to implement an instance of that complexity level (Fenton, 1997).
Table 9. Complexity weights for object points.
| Object type | Simple | Medium | Difficult |
| Screen | 1 | 2 | 3 |
| Report | 2 | 5 | 8 |
| 3GL component | - | - | 10 |
The weighted instances are summed to provide a single object point number. Reuse is then taken into account. Assuming that r% of the objects will be reused from previous projects, the number of new object points (NOP) is calculated to be:
NOP = (object points) x (100 – r) / 100
A productivity rate (PROD) is determined using Table 10 (Boehm et al, 1997).
Table 10. Average productivity rates based on developer’s experience and the ICASE maturity/capability.
| Developers' experience and capability | Very Low | Low | Nominal | High | Very High |
| ICASE maturity and capability | Very Low | Low | Nominal | High | Very High |
| PROD | 4 | 7 | 13 | 25 | 50 |
Effort can then be estimated using the following equation (Boehm et al, 1997):
E = NOP / PROD
The Early Design ModelThe Early Design model is used to evaluate alternative software/system architectures and concepts of operation. An unadjusted function point count (UFC) is used for sizing. This value is converted to LOC using tables such as those published by Jones, excerpted in Table 11 (Jones, 1996).
Table 11. Programming language levels and ranges of source code statements per function point.
| Language | Level | Min | Mode | Max |
| Machine language | 0.10 | - | 640 | - |
| Assembly | 1.00 | 237 | 320 | 416 |
| C | 2.50 | 60 | 128 | 170 |
| RPGII | 5.50 | 40 | 58 | 85 |
| C++ | 6.00 | 40 | 55 | 140 |
| Visual C++ | 9.50 | - | 34 | - |
| PowerBuilder | 20.00 | - | 16 | - |
| Excel | 57.00 | - | 5.5 | - |
The Early Design model equation is:
E = aKLOC x EAF
where a is a constant, provisionally set to 2.45.
The effort adjustment factor (EAF) is calculated as in the original COCOMO model using the 7 cost drivers shown in Table 12 (Boehm et al, 1997). The Early Design cost drivers are obtained by combining the Post-Architecture cost drivers shown in Table 13 (Boehm et al, 1997).
Table 12. Early Design cost drivers.
| Cost Driver | Description | Counterpart Combined Post-Architecture Cost Driver |
| RCPX | Product reliability and complexity | RELY, DATA, CPLX, DOCU |
| RUSE | Required reuse | RUSE |
| PDIF | Platform difficulty | TIME, STOR, PVOL |
| PERS | Personnel capability | ACAP, PCAP, PCON |
| PREX | Personnel experience | AEXP, PEXP, LTEX |
| FCIL | Facilities | TOOL, SITE |
| SCED | Schedule | SCED |
The Post-Architecture model is used during the actual development and maintenance of a product. Function points or LOC can be used for sizing, with modifiers for reuse and software breakage. Boehm advocates the set of guidelines proposed by The Software Engineering Institute in counting lines of code (Park, 1992). The Post-Architecture model includes a set of 17 cost drivers and a set of 5 factors determining the projects scaling component. The 5 factors replace the development modes (organic, semidetached, embedded) of the original COCOMO model.
The Post-Architecture model equation is:
E = aKLOC^b x EAF
where a is set to 2.55 and b is calculated as:
b = 1.01 + 0.01 x SUM(Wi)
where W is the set of 5 scale factors shown in Table 13 (Boehm et al, 1997).
Table 13. COCOMO II scale factors.
| W(i) | Very Low | Low | Nominal | High | Very High | Extra High |
| Precedentedness | 4.05 | 3.24 | 2.42 | 1.62 | 0.81 | 0.00 |
| Development/Flexibility | 6.07 | 4.86 | 3.64 | 2.43 | 1.21 | 0.00 |
| Architecture/Risk Resolution | 4.22 | 3.38 | 2.53 | 1.69 | 0.84 | 0.00 |
| Team Cohesion | 4.94 | 3.95 | 2.97 | 1.98 | 0.99 | 0.00 |
| Process Maturity | 4.54 | 3.64 | 2.73 | 1.82 | 0.91 | 0.00 |
The EAF is calculated using the 17 cost drivers shown in Table 14 (Boehm et al, 1997).
Table 14. Post-Architecture cost drivers.
| Cost Driver | Description | Rating | |||||
| Very Low | Low | Nominal | High | Very High | Extra High | ||
| Product | |||||||
| RELY | Required software reliability | 0.75 | 0.88 | 1.00 | 1.15 | 1.39 | - |
| DATA | Database size | - | 0.93 | 1.00 | 1.09 | 1.19 | - |
| CPLX | Product complexity | 0.70 | 0.88 | 1.00 | 1.15 | 1.30 | 1.66 |
| RUSE | Required reusability | 0.91 | 1.00 | 1.14 | 1.29 | 1.49 | |
| DOCU | Documentation | 0.95 | 1.00 | 1.06 | 1.13 | ||
| Platform | |||||||
| TIME | Execution time constraint | - | - | 1.00 | 1.11 | 1.31 | 1.67 |
| STOR | Main storage constraint | - | - | 1.00 | 1.06 | 1.21 | 1.57 |
| PVOL | Platform volatility | - | 0.87 | 1.00 | 1.15 | 1.30 | - |
| Personnel | |||||||
| ACAP | Analyst capability | 1.50 | 1.22 | 1.00 | 0.83 | 0.67 | - |
| PCAP | Programmer capability | 1.37 | 1.16 | 1.00 | 0.87 | 0.74 | - |
| PCON | Personnel continuity | 1.24 | 1.10 | 1.00 | 0.92 | 0.84 | - |
| AEXP | Applications experience | 1.22 | 1.10 | 1.00 | 0.89 | 0.81 | - |
| PEXP | Platform experience | 1.25 | 1.12 | 1.00 | 0.88 | 0.81 | - |
| LTEX | Language and tool experience | 1.22 | 1.10 | 1.00 | 0.91 | 0.84 | |
| Project | |||||||
| TOOL | Software Tools | 1.24 | 1.12 | 1.00 | 0.86 | 0.72 | - |
| SITE | Multisite development | 1.25 | 1.10 | 1.00 | 0.92 | 0.84 | 0.78 |
| SCED | Development Schedule | 1.29 | 1.10 | 1.00 | 1.00 | 1.00 | - |
Putnam developed a constraint model called SLIM to be applied to projects exceeding 70,000 lines of code. Putnam’s model assumes that effort for software projects is distributed similarly to a collection of Rayleigh curves. Putnam suggests that staffing rises smoothly during the project and then drops sharply during acceptance testing. The SLIM model is expressed as two equations describing relation between the development effort and the schedule. The first equation, called the software equation, states that development effort is proportional to the cube of the size and inversely proportional to the fourth power of the development time. The second equation, the manpower-buildup equation, states that the effort is proportional to the cube of the development time.
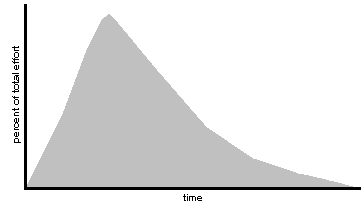
The Norden-Rayleigh CurveThe Norden-Rayleigh curve represents manpower as a function of time. Norden observed that the Rayleigh distribution provides a good approximation of the manpower curve for various hardware development processes (Pillai, 1997).
SLIM uses separate Rayleigh curves for design and code, test and validation, maintenance, and management. A Rayleigh curve is shown in Figure 1.

Figure 1. A Rayleigh curve.
Development effort is assumed to represent only 40 percent of the total life cycle cost. Requirements specification is not included in the model. Estimation using SLIM is not expected to take place until design and coding.
Several researchers have criticized the use of a Rayleigh curve as a basis for cost estimation (Pillai, 1997). Norden’s original observations were not based in theory but rather on observations. Moreover his data reflects hardware projects. It has not been demonstrated that software projects are staffed in the same way. Software projects sometimes exhibit a rapid manpower buildup which invalidate the SLIM model for the beginning of the project.
The Software EquationPutnam used some empirical observations about productivity levels to derive the software equation from the basic Rayleigh curve formula (Fenton, 1997). The software equation is expressed as:
Size = CE^1/3( t^4/3)
where C is a technology factor, E is the total project effort in person years, and t is the elapsed time to delivery in years.
The technology factor is a composite cost driver involving 14 components. It primarily reflects:
- Overall process maturity and management practices
- The extent to which good software engineering practices are used
- The level of programming languages used
- The state of the software environment
- The skills and experience of the software team
- The complexity of the application
The software equation includes a fourth power and therefore has strong implications for resource allocation on large projects. Relatively small extensions in delivery date can result in substantial reductions in effort (Pressman, 1997).
The Manpower-Buildup EquationTo allow effort estimation, Putnam introduced the manpower-buildup equation:
D = E / t^3
where D is a constant called manpower acceleration, E is the total project effort in years, and t is the elapsed time to delivery in years.
The manpower acceleration is 12.3 for new software with many interfaces and interactions with other systems, 15 for standalone systems, and 27 for reimplementations of existing systems.
Using the software and manpower-buildup equations, we can solve for effort (Fenton, 1997):
E = (S / C)^9/7 (D^4/7)
This equation is interesting because it shows that effort is proportional to size to the power 9/7 or ~1.286, which is similar to Boehm's factor which ranges from 1.05 to 1.20.
Criteria for Evaluating a ModelBoehm provides the following criteria for evaluating cost models (Boehm, 1981):
Problems with Existing Models
- Definition – Has the model clearly defined the costs it is estimating, and the costs it is excluding?
- Fidelity – Are the estimates close to the actual costs expended on the projects?
- Objectivity – Does the model avoid allocating most of the software cost variance to poorly calibrated subjective factors (such as complexity)? Is it hard to adjust the model to obtain any result you want?
- Constructiveness – Can a user tell why the model gives the estimates it does? Does it help the user understand the software job to be done?
- Detail – Does the model easily accommodate the estimation of a software system consisting of a number of subsystems and units? Does it give (accurate) phase and activity breakdowns?
- Stability – Do small differences in inputs produce small differences in output cost estimates?
- Scope – Does the model cover the class of software projects whose costs you need to estimate?
- Ease of Use – Are the model inputs and options easy to understand and specify?
- Prospectiveness – Does the model avoid the use of information that will not be well known until the project is complete?
- Parsimony – Does the model avoid the use of highly redundant factors, or factors which make no appreciable contribution to the results?
There is some question as to the validity of existing algorithmic models applied to a wide range of projects. It is suggested that a model is acceptable if 75 percent of the predicted values fall within 25 percent of their actual values (Fenton, 1997). Unfortunately most models are insufficient based on this criteria. Kemerer reports average errors (in terms of the difference between predicted and actual project effort) of over 600 percent in his independent study of COCOMO (Kemerer, 1997). The reasons why existing modeling methods have fallen short of their goals include model structure, complexity, and size estimation.
StructureAlthough most researchers and practitioners agree that size is the primary determinant of effort, the exact relationship between size and effort is unclear (Fenton, 1997). Most empirical studies express effort as a function of size with an exponent b and a multiplicative term a. However the values of a and b vary from data set to data set.
Most models suggest that effort is proportional to size, and b is included as an adjustment factor so that larger projects require more effort than smaller ones. Intuitively this makes sense, as larger projects would seem to require more effort to deal with increasing complexity. However in practice, there is little evidence to support this. Banker and Kemerer analyzed seven data sets, finding only one that was significantly different from 1 (with a level of significance of p=0.05) (Fenton, 1997). Table 15 compares the adjustment factors of several different models (Boehm, 1981).
Table 15. Comparison of effort equation adjustment factors.
| Model | Adjustment Factor |
| Walston-Felix | 0.91 |
| Nelson | 0.98 |
| Freburger-Basili | 1.02 |
| COCOMO (organic) | 1.05 |
| Herd | 1.06 |
| COCOMO (semi-detached) | 1.12 |
| Bailey-Basili | 1.16 |
| Frederic | 1.18 |
| COCOMO (embedded) | 1.20 |
| Phister | 1.275 |
| Putnam | 1.286 |
| Jones | 1.40 |
| Halstead | 1.50 |
| Schneider | 1.83 |
There is also little consensus about the effect of reducing or extending duration. Boehm’s schedule cost driver assumes that increasing or decreasing duration increases project effort. Putnam’s model implies that decreasing duration increases effort, but increasing duration decreases effort (Fenton, 1997). Other studies have shown that decreasing duration decreases effort, contradicting both models.
Most models work well in the environments for which they were derived, but perform poorly when applied more generally. The original COCOMO is based on a data set of 63 projects. COCOMO II is based on a data set of 83 projects. Models based on limited data sets tend to incorporate the particular characteristics of the data. This results in a high degree of accuracy for similar projects, but restricts the application of the model.
ComplexityAn organization’s particular characteristics can influence its productivity (Humphrey, 1990). Many models include adjustment factors, such as COCOMO’s cost drivers and SLIM’s technology factor to account for these differences. The estimator relies on adjustment factors to account for any variations between the model’s data set and the current estimate. However this generalized approach is often inadequate.
Kemerer has suggested that application of the COCOMO cost drivers does not always improve the accuracy of estimates (Kemerer, 1987). The COCOMO model assumes that the cost drivers are independent, but this is not the case in practice. Many of the cost drivers affect each other, resulting in the over emphasis of certain attributes. The cost drivers are also extremely subjective. It is difficult to ensure that the factors are assessed consistently and in the way the model developer intended (Fenton, 1997).
Calculation of adjustment factor is also often complicated. The SLIM model is extremely sensitive to the technology factor, however this is not an easy value to determine. Calculation of the EAF for the detailed COCOMO model can also be somewhat complex, as it is distributed between phases of the software lifecycle.
Size EstimationMost models require an estimate of product size. However size is difficult to predict early in the development lifecycle. Many models use LOC for sizing, which is not measurable during requirements analysis or project planning. Although function points and object points can be used earlier in the lifecycle, these measures are extremely subjective.
Size estimates can also be very inaccurate. Methods of estimation and data collection must be consistent to ensure an accurate prediction of product size. Unless the size metrics used in the model are the same as those used in practice, the model will not yield accurate results (Fenton, 1997).
Automated ToolsMany models are available as automated tools. These tools allow the planner to estimate cost and effort and to perform what if analyses for important project variables (Pressman, 1997).
CostarCostar is an estimation tool developed by Softstar Systems. Costar will produce estimates of a project's duration, staffing levels, effort, and cost based on the original COCOMO or COCOMO II models. Planners can adjust the estimate to arrive at an optimal project plan. The main screen is shown in Figure 2.
Figure 2. Costar main screen.
SLIMPutnam has extended the SLIM model to include an automated tool. The SLIM tool was developed by Quantitative Software Management. SLIM produces the chart shown in Figure 3.
Figure 3. SLIM manpower distribution.
CheckpointCheckpoint is a tool developed by Software Productivity Research. Checkpoint predicts effort at four levels: project, phases, activity, and task. Checkpoint facilitates the comparison of actual and estimated performance to various industry standards included in an internal estimation knowledge base.
Summary and ConclusionsSoftware cost estimation is an important part of the software development process. Models can be used to represent the relationship between effort and a primary cost factor such as size. Cost drivers are used to adjust the preliminary estimate provided by the primary cost factor. Although models are widely used to predict software cost, many suffer from some common problems. The structure of most models is based on empirical results rather than theory. Models are often complex and rely heavily on size estimation. Despite these problems, models are still important to the software development process. Model can be used most effectively to supplement and corroborate other methods of estimation.