| 1) (GV) Num pátio existem automóveis e bicicletas. O número total de
rodas é 130 e o número de bicicletas é o triplo do número de automóveis. Então, o
número total de veículos que se encontram no pátio é:
a) 50 ......................................b)
42
c) 52 ......................................d) 54 ......................................e) 62
|
| 2) (GV) A quantia de R$ 2.100,00 foi distribuída entre 4 pessoas do
seguinte modo: a segunda recebeu a metade da primeira; a terceira recebeu a metade da soma
da primeira com a segunda; e a quarta a metade da terceira. Quanto recebeu a segunda
pessoa?
a) R$ 600,00 ..........................b) R$ 200,00
............................. c) R$ 500,00
b) R$ 300,00 ..........................e) R$ 400,00
|
| 3) (FUVEST) O dobro de um número, mais a sua terça parte, mais a sua
quarta parte somam 31. Determine o número. |
| 4) (FUVEST) Dois quintos do meu salário são reservados para o aluguel, e a
metade do que sobra, para a alimentação. Descontados o dinheiro do aluguel e da
alimentação, coloco um terço do que sobra na poupança, restando então R$ 1.200,00
para gastos diversos. Qual é o meu salário? |
| 5) (FUVEST) Subtraindo-se 3 de um certo número, obtém-se o dobro da
sua raiz quadrada. Qual é esse número? |
| 6) (FUVEST) A soma de um número com sua quinta parte é 2. Qual é o
número? |
| 7) (PUC-SP) Para produzir um objeto, uma firma gasta R$ 1,20 por
unidade. Além disso, há uma despesa fixa de R$ 4.000,00, independente da quantidade
produzida. O preço de venda é de R$ 2,00 por unidade. Qual é o número mínimo de
unidades, a partir do qual a firma começa a ter lucro?
a) 1.800 ......................................b)
2.500 ......................................c) 3.600
d) 4.000 ...................................... e) 5.000
|
| 8) (UFCE) Dois tipos de comprimidos I e II são fabricados de modo que
cada comprimido do tipo I contenha 10 unidades de vitamina A e 5 unidades de vitamina B e
cada comprimido do tipo II contenha 3 unidades de vitamina A e 2 unidades de vitamina B.
Calcular o número total de comprimidos I e II (juntos) que uma pessoa deve ingerir de
modo a absorver 35 unidades de vitamina A e 20 unidades de vitamina B. |
| 9) (FUVEST) Um copo cheio de água pesa 325 g. Se jogarmos metade da
água fora, seu peso cai para 180 gramas. O peso do copo vazio é:
a) 20 g ......................................b) 25 g ......................................c)
35 g
d) 40 g ......................................e) 45 g
|
| 10) (UFGO) Diminuindo-se 6 anos de idade de minha filha obtém-se os 3/5
de sua idade. A idade de minha filha, em anos, é:
a) 9 ......................................b)
10 ...................................... c) 12
d) 15 ................................... e) 18
|
| 11) (UFSC) Um fazendeiro repartiu 240 reses entre seus três herdeiros
da seguinte forma: o primeiro recebeu 2/3 do segundo, e o terceiro tanto quanto o primeiro
e o segundo juntos. Quanto recebeu o primeiro herdeiro? |
| 12) (FUVEST) A soma dos quadrados de dois números positivos é 4 e a
soma dos inversos de seus quadrados é 1. Determine:
a) o produto dos dois números;
b) a soma dos dois números.
|
| 13) (FEP-PA) Um número é composto de dois algarismos cuja diferença
é 3. Escrito na ordem inversa obtém-se 4/7 do número dado. O número dado é:
a) 96 ......................................b) 74 ......................................
c) 69
d) 63 ......................................e) 52
|
| 14) (UNICAMP) Ache dois números inteiros positivos e consecutivos
sabendo que a soma de seus quadrados é 481. |
| 15) (GV) A quantia de R$ 4.000, 00 deveria ser repartida para um certo
número de crianças, No entanto, quatro crianças deixaram de comparecer aumentando com
isso em R$ 50,00 a quantia para cada uma das crianças restantes. Qual era o número
inicial de crianças?
a) 10 ......................................
b) 32 ...................................... c) - 3
d) 66 ...................................... e) n.d.a.
|
| 16) (GV) A soma de dois números é 400. Dividindo-se o maior por 36 e o
menor por 28 obtemos o mesmo quociente e o resto zero. Então, a raiz quadrada do maior
adicionada à quinta parte do menor resulta em:
a) 64 ......................................
b) 8 ...................................... c) 40
d) 50 ...................................... e) n.d.a.
|
| 17) (UNICAMP) Um funcionário teve seu salário reajustado em 6/10
daquilo que recebia antes desse reajuste, e passou então a ganhar R$ 8.600,00. Qual o seu
salário antes do aumento? |
| 18) (UNICAMP) Para transformar uma temperatura dada em graus Fahrenheit
(ºF) para seu valor em graus Celsius (ºC), procede-se da seguinte forma: subtrai-se 32
do número que exprime a temperatura em ºF e multiplica-se o resultado por 5/9. Qual é a
temperatura que é expressa pelo mesmo número tanto em ºF quanto em ºC? |
| 19) (GV) Daqui a 12 anos eu terei o triplo da idade que você tinha há
12 anos atrás. Se hoje eu tenho 15 anos que idade você tera daqui a 12 anos?
a) 12
anos .................................b) 21 anos ................................. c) 15 anos
d) 33 anos ................................ e) 27 anos
|
| 20) (FATEC) Uma loja vendeu 112 pneus para 37 veículos entre
"Fuscas" e motos. Somente dois "Fuscas" trocaram também o pneu de
estepe. Quantas motos trocaram pneus? |
| 21) (UNICAMP) Uma bola elástica, abandonada de certa altura, volta 8/9
da altura original após atingir o solo. Calcule a altura original considerando que,
depois de dois toques no solo, ela volta a uma altura de 80 cm. |
| 22) (VUNESP) João e Tomás partiram um bolo retangular. João comeu a
metade da terça parte e Tomás comeu a terça parte da metade. Quem comeu mais?
a)
João, porque a metade é maior que a terça parte.
b) Tomás.
c) Não se pode decidir porque não se conhece o tamanho do bolo.
d) Os dois comeram a mesma quantidade de bolo.
e) Não se pode decidir porque o bolo não é redondo.
|
| 23) (FUVEST) No vestibular FUVEST 90 exigia-se,
dos candidatos à carreira de administração, a nota
mínima 3,0 em Matemática e em Redação.
Apurados os resultados, verificou-se que 175 candidatos foram
eliminados em Matemática e 76 candidatos forma eliminados em
Redação. O número total de candidatos eliminados
por essas duas disciplinas foi 219.
Qual foi o número de candidatos eliminados apenas pela
Redação?
a) 24 ...................................... b) 143 ...................................... c) 32
d) 44 ......................................e) 99
|
24) (FUVEST) A tabela abaixo fornece os valores unitários do peso,
volume e preço de três tipos de produtos A, B e C.
| |
A
|
B
|
C
|
|
Peso (kg)
|
2
|
3
|
5
|
|
Volume (litros)
|
2
|
5
|
4
|
|
Preço (US$)
|
4
|
8
|
10
|
a) Calcule o valor total do peso, volume e preço do seguinte pedido de
mercadorias:
|
A
|
100 unidades
|
|
B
|
200 unidades
|
|
C
|
50 unidades
|
b) Calcule o número de unidades de cada um dos produtos A, B e C
num despacho com os seguintes valores totais:
|
Peso
|
4.500 kg
|
|
Volume
|
5.300 litros
|
|
Preço
|
10.000 US$
|
|
| 25) (PUCC) Considere um número real qualquer, diferente de zero. Some
esse número com 3, multiplique a soma por 5, subtraia 15 do produto e divida o que resta
pelo próprio número. É correto afirmar que o resultado desses cálculos
a) depende do
número considerado. ......................................
b) é sempre 1. .....................................
c) é sempre 5.
d) pode ser negativo.
.e) é um número maior que o número considerado.
|
| 26) (PUCC) Numa certa cidade, os taxímetros marcam, nos percursos sem
parada, uma quantia inicial de 4 UT (Unidade Taximétrica) e mais 0,2 UT por quilômetro
rodado. Se, ao final de um percurso sem paradas, o taxímetro registrava 8,2 UT, o total
de quilômetros percorridos foi
a) 15,5 ....................................
b) 21 ...................................... c) 25,5
d) 27 ...................................... e) 32,5
|
| 27) (GV) Determinar quatro números reais de modo que suas somas, três
a três, sejam 10, 11, 12 e 13. |
| 28) (IME) A coleção de selos de Roberto está dividida em três
volumes. Dois décimos do total de selos estão no primeiro volume, alguns sétimos do
total estão no segundo volume e 303 selos estão no terceiro volume. Quantos selos
Roberto tem? |
| 29) (VUNESP) Segundo dados de um estudo, 100 g de soja seca contêm 35 g
de proteínas e 100 g de lentilha seca contêm 26g de proteínas. Suponhamos que uma
pessoa, objetivando ingerir 70 g de proteínas por dia, se alimentasse apenas com esses
dois produtos. Se num certo dia sua alimentação incluísse 140 g de soja seca, calcular
a quantidade de lentilha que deveria incluir. |
| 30) (FUVEST) Encontre todos os conjuntos de três números inteiros
consecutivos cuja soma é igual ao seu produto. |
| 31) Uma caixa d’água com capacidade de 3000 litros está com 1000 litros
de água. Outra de 1000 litros, está com 300 litros. Cada uma delas está recebendo 10
litros de água por minuto. Em quantos minutos a primeira caixa terá exatamente o dobro
da quantidade de água da segunda? |
32) (PUCC) A pessoa A, generosamente dá  do que possui à pessoa B. Esta, sentindo-se rica, perde 20 mil
jogando pôquer e fica com a mesma quantia que A. Quanto tinha a pessoa A no
início da história, se A e B, juntas, possuíam 140 mil?
a) R$ 96.000,00
......................................b) R$ 90.000,00
c) R$ 84.000,00 ......................................d)
R$ 72.000,00
e) R$ 60.000,00
|
| 33) (UNICAMP) O IBGE contratou um certo número de entrevistadores para
realizar o recenseamento em uma cidade.
Se cada um deles recenseasse 100 residências,
60 delas não seriam visitadas. Como, no entanto, todas as residências foram visitadas e
cada recenseador visitou 102, quantas residências tem a cidade?
|
| 34) Num certo momento, se 10% dos homens de uma cidade A fossem
mulheres, o número de homens e mulheres da cidade seria igual. Após um certo tempo,
tendo nascido 40 crianças, verificou-se que o número de homens igualou-se ao número de
mulheres. No período, não foi registrada nenhuma morte e nenhum caso de mudança de
pessoas da cidade ou para a cidade.
a) Seja x o número de homens e y, o
de mulheres no início. Quais são os possíveis valores de x e y?
b) Seja t o número de meninos que nasceram no período. Quais são os
possíveis valores de t?
|
| 35) Estando todos os irmãos reunidos à mesa, um menino diz:
- Vejo tantos
irmãos quanto irmãs.
Uma menina diz:
- Vejo que o número de meus irmãos é o dobro do de minhas irmãs.
Quantos são os meninos? E as meninas?
|
| 35) Eu tenho duas vezes a idade que tu tinhas quando eu tinha o que tu tens.
Quando tiveres a idade que eu tenho, soma de nossas idades será 45 anos. Quantos anos
tenho? |
| 36) As despesas de um condomínio totalizam R$ 36.000,00. Cinco dos
condôminos, não dispondo de dinheiro para pagar, obrigam os demais condôminos, além de
sua parte, a pagar um adicional de R$ 240,00 cada um. Qual o número total de pessoas do
condomínio? |
| 37) O resto por falta, da raiz quadrada de um inteiro positivo, é 14 e o resto
por excesso é 9. Achar esse inteiro. |
38) Aldo viveu, nesta ordem, 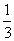 de sua vida
em Jundiaí,  em Pedreira, 12 anos em Amparo, a
metade do resto em São Paulo e está atualmente morando em Campinas há tantos anos
quanto morou em Pedreira.
Pergunta: Em que cidade ele fez 40 anos?
|
| 39) Duas camponesas levaram um total de 100 ovos ao mercado. Uma delas, tinha
mais mercadoria que a outra, no entanto, recebeu por ela a mesma quantidade de dinheiro
que a outra.
Uma vez vendidos todos, a primeira camponesa disse à segunda: "Se eu
tivesse levado a mesma quantidade de ovos que você, teria recebido 15 moedas". A
segunda respondeu: "Se eu tivesse vendido os ovos que você tinha, teria recebido 6
2/3 moedas". Quantos ovos tinha cada uma?
(Introdução à álgebra - Leonard Euler)
|
| 40) Um vendedor de maçãs vendeu ao primeiro cliente, metade das maçãs que
tinha, mais meia maçã; ao segundo cliente, vendeu metade do restante, mais meia maçã e
assim sucessivamente até o quinto cliente, quando então acabaram as suas maçãs.
Quantas
maçãs o vendedor tinha inicialmente?
|
|
|
|
|