PGP (Pretty Good Privacy) que l'on pourrait traduire en français par "assez bonne confidentilalité" est un système de chiffrement hybride qui combine un algorithme à clé publique (asymétrique) avec un algorithme à clé secrète (symétrique) pour donner un chiffrement combinant la vitesse de la cryptographie conventionnelle avec les avantages considérables de la cryptographie à clé publique. En ce qui concerne l'utilisateur, PGP se comporte comme un système de chiffrement à clé publique, où une paire de clés (se composant d'une clé publique et d'une clé privée) est mathématiquement produite. Vous pouvez crypter un message avec une clé et le décrypter avec l'autre (l'une ou l'autre clé peut être utilisée pour le cryptage) mais le message codé ne peut pas être décrypté en utilisant la même clé que celle qui a été employée pour le crypter (cryptage asymétrique). D'une façon générale vous rendez disponible votre clé publique à n'importe qui veut vous envoyer un message crypté. L'expéditeur crypte son message avec votre clé publique - ils ne peuvent plus alors décrypter leur message et ni quiconque d'autre que vous. La seule personne qui peut décrypter le message est vous, c'est-à-dire la personne qui a la clé privée qui est associée à la clé publique. Il est clair que la clé privée doit être maintenue secrète par son propriétaire. Le grand avantage de ce genre de cryptographie est que, à la différence de la cryptographie conventionnelle à clé secrète, il n'est pas nécessaire de trouver un moyens sûr pour communiquer la clé de chiffrement au destinataire de votre message. Un autre dispositif utile de tels systèmes de chiffrement à clé publique est la capacité de " signer " des messages en les cryptant avec votre clé privée. N'importe qui peut alors décrypter le message avec votre clé publique, et le destinataire peut être sûr que seul le propriétaire de cette clé publique a pu crypter le message (avec la clé privée correspondante).

PGP peut être employé pour produire des signatures électroniques (ou empreintes digitales). Une signature électronique est un bloc de données qui est créé en utilisant une certaine clé privée et qui "résume le message original", et il n'y a qu'une clé publique (associée à la clé privée) qui peut être employée pour vérifier que la signature a été vraiment produite en utilisant la clé privée correspondante. L'algorithme employé pour produire la signature est tel que sans connaître la clé privée, il n'est pas possible de créer une signature qui soit vérifiée comme valide avec la clé publique. Des signatures électroniques sont employées pour vérifier qu'un message vient vraiment de l'expéditeur voulu et que le contenu du message n'a pas été modifié (considérant que seul l'expéditeur connaît la clé privée associée à sa clé publique).Une signature électronique d'un document est créée en calculant un "résumé" du message avec un algorithme et en l'enchaînant avec des informations sur le signataire en utilisant un algorithme approprié. La chaîne de caractères résultante est alors cryptée en utilisant la clé privée du signataire. Le bloc chiffré résultant est la signature électronique ou empreinte digitale. Pour vérifier une signature, on décrypte la signature électronique en utilisant la clé publique de la personne qui a envoyé le message signé. Si la clé publique décrypte correctement la signature électronique du message (un algorithme vérifie le message transmis et le "résumé" produit lors de la signature pour vérifier qu'aucune modification n'a été apportée au message original), la signature est reçue comme valide.

Il reste encore à être sûr que la clé publique dont on dispose est bien celle d'une personne qui prétend que c'est la sienne. C'est encore un point faible des systèmes de cryptographie à clé publique. On peut y contribuer en faisant signer la combinaison de la clé et des informations sur son propriétaire par d'autres personnes (signatures par des clés de confiance, certification de clé). C'est le concept de confiance utilisé par exemple dans PGP.

Lorsque PGP est installé sur votre ordinateur, vous allez générer une paire de clés comprenant la clé publique et la clé privée . La clé privée doit être gardée soigneusement secrète. Chaque personne qui veut vous faire parvenir un message crypté avec PGP a besoin de connaître votre clé publique. Le message est alors crypté par l'expéditeur avec la clé publique du destinataire et lui est envoyé. Seul le destinataire peut décrypter le message codé avec sa clé privée.

Chaque personne qui veut envoyer un message crypté par PGP doit avoir en sa possession un "trousseau de clés" qui, à part sa propre paire de clés (publique et privée), comprendra les clés publiques des destinataires de messages cryptés. Le trousseau de clés est enregistré sur le disque de son PC en association avec les adresses e-mails des propriétaires des clés.

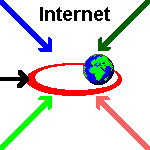
Lorsque quelqu'un veut envoyer un message crypté par PGP à Charlie, il a besoin de la clé publique de Charlie. Il peut la recevoir par e-mail directement de Charlie ou aller à une adresse donnée sur Internet où Charlie l'a déposée (par exemple sur la Home Page de Charlie). Lorsque quelqu'un veut envoyer un message crypté par PGP à Snoopy, il peut aller chercher sa clé sur un serveur de clés, adresse Internet regroupant les clés publiques de nombreuses personnes ou la recevoir par e-mail directement de Snoopy. Lorsque quelqu'un veut envoyer un message crypté par PGP à Lucy, il ne peut que la recevoir par e-mail directement de Lucy.

RSA utilise l'exponentiation modulaire (^ est utilisé pour symboliser l'exponentiation) pour crypter et décrypter des messages basés sur des textes convertis en forme numérique.

La fonction de cryptage de RSA est la suivante: C = T^U mod N, où T est le texte en clair, C est le texte crypté et U la clé publique et N un nombre entier > U et < T^U. En d'autres termes T est élevé à la puissance de U modulo N . (a mod b indique le reste de la division de a par b).

La fonction de décryptage de RSA est la suivante: T = C^R mod N, où T est le texte en clair, C est le texte crypté, R la clé privée et N un nombre entier > R et < C^R.

Les clés U et R doivent être produites tels que U est l'inverse de R eu égard à l'exponentiation modulaire, c'est-à-dire qu'il est nécessaire que (T^U mod N)^R mod N = (T^UR) mod N = T.

L'exponentiation modulaire est une fonction asymétrique f(x) dans le sens que si l'on a g = f(x), il n'est pas possible de trouver f-1(x) (plusieurs solutions). Exemple: posons T = 2, U = 3 et N = 5. T^U = 2^3 = 8 et 8 mod 5 = 3 = C. En connaissant U et C, il n'est pas possible de retrouver T de manière univoque: ainsi on a 3 = 2^3 mod 5 mais aussi 3 = 7^3 mod 5, etc.