About Demo
Partially Randomized Systems and Spectral Analysis
1. Toy Model
Any system can be characterized by correlations (spacial- and time-like) of its elements. A powerful mechanism to reveal these correlations is a spectral analysis.
Let us start with a very simple system in which Black and White balls form a chain structure. The formulation of the problem is consistent with a random distribution of these Blacks and Whites constrained with definite concentrations of both sorts.
In fact, a true situation with randomly distributed balls is highly difficult for realization: but this question is beyond the scope of this Demo. We can easily imagine that the balls are partly randomized, that means, partly correlated.
More important are applications for ball ensembles, consisting of more than two sorts of balls. Because their consideration (not academic, but more, or less realistic) needs to involve the transfer matrix ideas, I tried to avoid such a generalization here.
Let us start to think in terms of clusters. If there are no correlations, the frequency of appearance of the Black-balls cluster, containing of (n + 1) Black balls, and no Whites, is the frequency for the n-Black-balls cluster, multiplied by c , if c is the concentration of Black balls and the balls are randomly distributed along the chain. For White balls such a recursion should include a factor (1 – c).
It should be intuitively clear, that frequencies decay exponentially with n. Indeed, if no correlations are introduced, but the only parameter is concentration, the frequencies are true exponentially decaying functions. For a partly correlated system, one, or both frequencies might be different from an exponential decay on not-too-long scale: Moreover, a frequency might increase with a cluster length before an exponential decay will develop.
Microscopic (Fourier) analysis of the system can be done if we ascribe a "scattering" amplitude exp(i ql) to a Black ball located at the chain site l. Then the total amplitude F will be the sum over individual amplitudes of Black balls. However, the amplitudes are not measured, but the quadratic form K = F F* is the observable quantity. Important fact about the structure factor of a disordered system is that this quantity should be proportional to the system length.
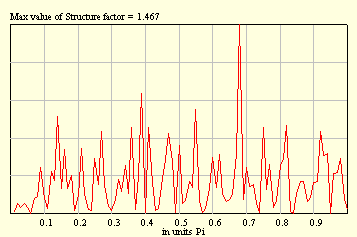
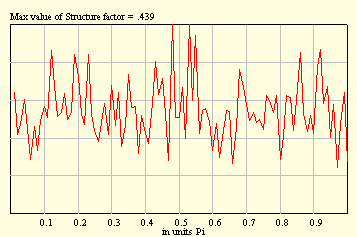
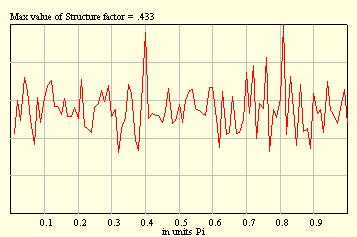

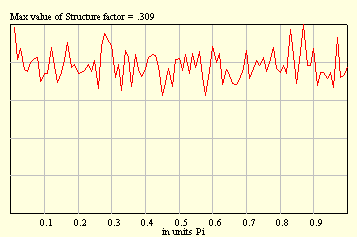
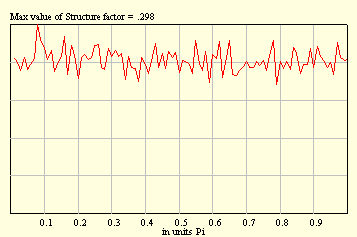
Well, this is not a difficult problem to calculate the structure factor analytically. And, in fact, the rigorous result is 1/4.
That is important to mention that performing averaging over random configurations we meet with the so-called sampling. For example, if you take, say, ten samples with 1000 balls in each, in this case statistics will be better as compared with that one due to one sample with 10000 balls. Two pictures below illustrate this fact.


2. How to make a bridge to Phase Separation?
Let us modify a randomization process, accepting the following rules:
- A Black ball is tried to be placed into the chain, substituting for a White ball, until the concentration of Blacks reaches a desired value (that’s a usual element of a traditional randomization scheme);
- If a site which is tried for a Black ball is surrounded by two White balls, then this event is accepted only probabilistically ;
- If a site which is tried for a Black ball has at least one Black ball as a nearest neighbor, then this event is accepted.
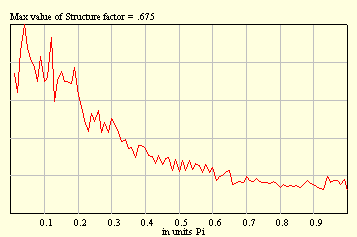
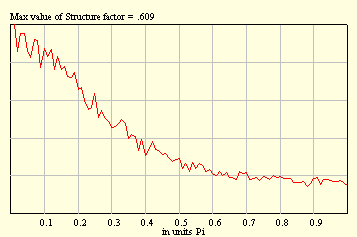
It is possible to apply a process in which Black and White balls tend to form clusters of minimal sizes. In this case a process of substitution should satisfy the following constraints:
- If a site which is tried for a Black ball is surrounded by two White balls, then this event is accepted;
- If a site which is tried for a Black ball has at least one Black ball as a nearest neighbor, then this event is accepted only probabilistically.
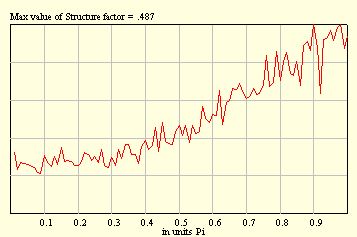
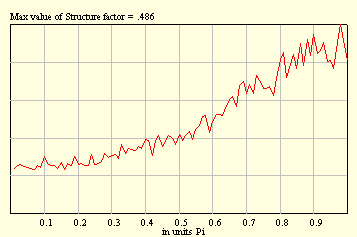
From the figures below, a tendency to form long and short clusters whose fingerprints are maxima at q = 0, and p, becomes evident.
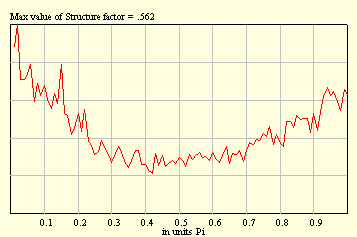
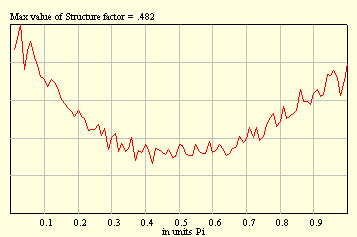
-
Return to
- Page Central,
- Roadmap,
- Professional Resume.