The Complexity of the
Collatz problem
The Collatz problem is a very simple, well-known and unresolved problem
of number theory. It can be expressed like this:
1. Take any integer number.
2. Divide it by 2. If the division is exact, repeat step 2.
3. If it isn't, multiply it by 3, add 1 and go to step 2.
For example, if you start with 7, you'll get:
7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
The question is: does this journey always end with 1? Computers have
calculated this for numbers up to millions, and they've always ended at
1. But it has never been proven it has to be so for every number. Many
mathematicians have attacked the problem with no result. Legend says scientists
in Los Alamos spent a good deal of their time with it, instead of working
in the atomic bomb! It was even rumored it was a Russian sabotage.
I haven't solved it, I've got no idea about how to solve it, but I
have a good insight of how complex it can be. Let's consider a generalized
version of the problem:
1. Take any Gauss integer
2. Divide it by another called a. If the division is exact,
repeat step 2.
3. If it isn't, multiply it by b, add c and go to step
2.
What's a Gauss integer? It's a complex number whose real and imaginary
parts are integer. Now, you can feed the problem to Fractint and see how
long it takes to get to 1, -1, i, -i, 1+i, 1-i, -1+i or -1-i. (If you don't
know what are complex numbers or Fractint, it's a good moment to learn.
Click here).You
get some marvellous plots like these (click on the thumbnails to see a
larger image):
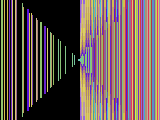
a=2, b=3, c=1
(the classical Collatz) |

a=1+i, b=i, c=i
|
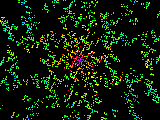
a=2+i, b=i, c=1
|

a=1+2i, b=1, c=1 |
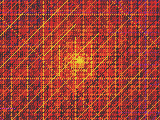
a=8+8i, b=1+i, c=2+2i |

a=20+20i, b=1, c=1+i |
This is the code you should write in the fractint.frm file to explore
it yourself:
Collatz {
z=scrnpix-scrnmax/2:
t=z/p1
test= (t==floor(t))
z=test*t+(1-test)*(p2*z+p3)
|z|>2
}
(Take p1 as a, p2 as b, and p3 as c)
What I love of this problem is the incredibly varied kinds of plots
you can get. If you find something interesting, e-mail me: lusina@redestb.es
Back to math page