GEOMETRIC FUNCTIONS
The concept of geometric functions is a subject of great difficulty when first encountered by the student in the classroom. Perhaps that difficulty is caused because the subject is considered by instructor and student alike as a new form of reality, rather than as an imaginary game.
The ultimate simplicity becomes apparent when it is recognized that geometric functions are simply a different way to present the concept of fractional numbers.
There are two primary geometric ‘functions’ named the ‘sine’ and the ‘cosine’. These are simply code words which refer ratio of the vertical and horizontal component length of a line that is one unit long as the angular inclination of that line is varied from horizontal to vertical orientation.
One end of the line of unit length is imagined to be located at the origin of a cartographic coordinate system. The other end of that same line is then imagined to rotate from the horizontal position to the right of the origin of the coordinate system through a range of ‘angles’ from zero ‘degrees’ to 360 ‘degrees’.
All other geometric functions are simply imaginary ratios or manipulations involving the lengths which have been given the names of sine, the cosine, and the unit of length associated with that line from which the sine and cosine ratios were themselves defined.
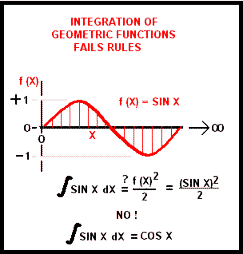Another problem of inconsistency occurs when an attempt is made to apply the general rules of integral calculus to geometric (or trigonometric) functions. And as was true for the creation of
‘logarithmic’ functions, a new set of rules had to be created in order to perform calculus operations involving geometric functions. For example, if the generalized rules of integration were applied to the function f (X) = sin X, then the associated value would be an area equal to the square of the sin divided by 2. But that is not the correct result because integration of a pure number such as indicated by sin X does not result in an area, and in any case, the resultant numbers are not correct.
Hence it was necessary to establish an entire new set of mathematical equations which had to be memorized in order to determine the desired value for integration of geometric type functions.
skip to SIGNIFICANCE
back to Calculus
back to Logarithms
return to DIALOG page
Home Index