-
La creación de la teoría de conjuntos
se debe al matemático alemán Georg Cantor (1845-1918).
- Las coordenadas cartesianas las inventó el
francés Renato Descartes (Cartesius en latín), en el
siglo XVII.
-
Los números naturales se conocen desde la
época más remota. Los babilonios sintieron necesidad de
usar el cero; al principio el cero era un espacio en blanco,
así el número 7 5 significaba 7 centenas, ninguna
decena y 5 unidades. Al pasar el tiempo se utilizó el
símbolo 0 como círculo para rellenar los espacios en
blanco, por tanto el número anterior se escribía 705,
como lo hacemos actualmente.
-
La invención del 0 se debe a los hindúes en
el siglo IX, fueron los árabes los que lo introdujeron en
Europa. Al parecer, el primer matemático importante que hizo
uso del signo 0 fue el árabe Muhammad ibn al-Khwarizmi, en el
810 de nuestra era, aunque no adquirió su actual significado
hasta el siglo XVII.
-
El símbolo de la raíz tiene su origen en una
r inicial de la palabra latina radix.
El símbolo de la raíz, aparece por primera vez en el
libro de álgebra publicado en alemán en 1525, de
Christoff Rudolff.
-
El número raíz cuadrada de dos aparece por primera
vez al aplicar los griegos el teorema de Pitágoras para
calcular la diagonal de un cuadrado de lado 1.
-
La primera edición latina del libro Los Elementos de
Euclides apareció en 1482 con la invención de la imprenta.
-
De los tres pueblos orientales (chino, indio y árabe) que
influyeron en el progreso de las matemáticas, fueron los indios
los más importantes en aportaciones originales: conservaron
los trabajos de los griegos, inventaron el sistema de
numeración decimal, el uso del cero como símbolo
operatorio, establecieron diferencias entre números enteros
positivos y negativos, que interpretaron como créditos y débitos.
-
Los problemas de interés los conocían los indios,
pero fueron los árabes los que los introdujeron en España.
-
Parece ser que las letras de cambio fueron inventadas por
los judíos en el siglo VII tras ser expulsados de Francia.
Otros investigadores opinan que nacieron de las relaciones entre
Grecia y Roma.
-
Cuando decimos que un objeto de oro tiene 16 quilates,
significa que de 24 partes del objeto, 16 son de oro. Sirve para
medir la ley; en este caso el objeto de oro tiene una ley de 16 quilates.
También se utiliza el quilate como unidad de masa de
piedras preciosas; se llama quilate métrico y su valor es de
200 miligramos.
-
El origen de los signos + y - no se conoce con certeza. Hay
varias opiniones. Una de ellas supone que surgieron de las marcas
hechas con tiza en las cajas de mercaderías, por los
comerciantes alemanes del siglo XV, para indicar las diferencias de
peso en más o en menos según un patrón establecido.
-
El signo = para las igualdades fue utilizado por primera vez por
el inglés Robert Recorbe en 1557 apareciendo por primera vez
en su libro "El aguzador del ingenio", siendo el primer
tratado inglés de álgebra. Según el autor,
eligió ese símbolo porque dos cosas no pueden ser
más iguales que dos rectas paralelas.
El símbolo se generalizó hacia finales del siglo
XVII. Descartes utilizó un signo semejante al símbolo
del infinito.
-
En el año 1761, Lambert (matemático alemán)
demostró que ¶ es un número irracional, es
decir, no es expresable mediante una fracción de números
enteros.
-
El símbolo ¶ fue usado en 1647 por William Oughtred,
para representar la circunferencia de un círculo. William
Jones en 1706 en Sypnosis palmariorum mathesios, fue el primero que
lo utilizó para la relación entre la longitud de la
circunferencia y su diámetro. Sin embargo fue Leonhard Euler
quien lo popularizó en 1748.
-
El número irracional ¶ es un número trascendente,
por no ser solución de ninguna ecuación de
coeficientes enteros; esto lo demostró Ferdinand Lindemann
(matemático alemán, 1852-1939).
-
La regla de los signos de la multiplicación:
-
El símbolo . para la multiplicación fue utilizado
por Thomas Harriot, pero quien lo popularizó fue Leibniz.
-
Una propiedad curiosa del número 12345679 es que los
múltiplos que resultan al multiplicarlo por: 9, 18, 27, 36,
45, 54, 63, 72 y 81, se escriben con una sola cifra.
-
La divisibilidad por 2, 5, 3 y 9 ya era conocida por los
indios bastante antes de nuestra era. En cambio, el criterio de
divisibilidad por 11 no se conoció hasta el siglo XVI.
-
La división sexagesimal se debe a los caldeos.
-
La división centesimal se inventó con el
sistema métrico decimal a finales del siglo XVIII.
-
El Sistema Métrico Decimal que mide longitudes,
volúmenes, superficies, capacidades y masas, fue aprobado en
el año 1791 por la Academia de Ciencias de París.
Debido al desarrollo de la técnica y la ciencia ha habido
modificaciones importantes en el S.M.D. y se han introducido nuevas
unidades de medida.
España adoptó el sistema por la Ley de 8 de junio de 1892.
Se tomó como unidad fundamental el metro y así
se inició el Sistema Métrico Decimal.
-
Existe el número googol que es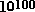 
;
el nombre se lo puso un niño de 9 años, sobrino del
matemático Kasner. Es un número muy grande, si
asignamos a una gota de agua un espesor de 2 mm., habría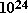 
gotas de agua en el Mediterráneo.
-
El triángulo perfecto o sagrado, de lados 3, 4 y 5
unidades, fue usado por los egipcios para trazar ángulos
rectos. En sus papiros se observan los tenedores de cuerdas,
que fijaban los límites de las parcelas después de las
inundaciones del Nilo, construyendo con cuerdas triángulos
rectángulos y fijando direcciones perpendiculares. Los
arquitectos de algunas dinastías persas también usaron
estos conocimientos para trazar los tejados de sus edificios.
-
El primer mapa con carácter científico se
debe al griego Dicearc (IV-III a.C.). Dividió la Tierra
trazando una línea horizontal que salía de las Columnas
de Hércules (Estrecho de Gibraltar), pasando por Sicilia, el
Peloponeso y Asia Menor. También trazó una línea
perpendicular a la primera que pasaba por la actual Asswan (Egipto).
De esta manera, cualquier punto en tierra o en mar se identificaba
con dos números: la distancia a la línea horizontal y a
la vertical. En el siglo XVII y basándose en esta idea surge
la Geometría Analítica.
-
El origen de la Trigonometría se debe a los indios y
egipcios; pero los verdaderos impulsores fueron los árabes que
por razones religiosas se les plantearon problemas de
orientación y determinación de fechas y horas,
perfeccionando aspectos astronómicos y con ello la Trigonometría.
-
Thales fundó en la ciudad griega de Mileto (s. VI a.
d. C.) la primera escuela que organizó los estudios de
Geometría. Murió repentinamente mientras que
asistía a los Juegos Olímpicos.
-
Lo que hoy conocemos como ecuaciones lineales,
aparecían en el papiro Rhind, escrito por el sacerdote egipcio
Ahmes (2000 años a. J.C.), representando la incógnita
con un ibis (ave tropical) escarbando en el suelo.
-
El uso de las letras x, y, z para representar incógnitas
y las primeras del abecedario para valores conocidos, aparece en el
libro "La Geometrie" de Descartes. Se cuenta que cuando el
libro se estaba imprimiendo y debido a la gran cantidad de ecuaciones
que tenía, se quedaban sin letras, el editor le preguntó
a Descartes si podía emplear otras letras para las
ecuaciones. Descartes le respondió que era indiferente las
letras que utilizase en las ecuaciones. El editor eligió la x porque
en francés esa letra se utiliza poco.
Otros autores afirman que la x se usó como abreviatura de
la palabra árabe shei (cosa).
Diofanto usaba una letra griega con acento para representar
una cantidad desconocida.
- El calendario es el conjunto de normas para contar el tiempo.
La Tierra tarda 365'2422168... días en su movimiento de
rotación alrededor del Sol, aunque se toman 365 días
que es el año civil.
Para compensar el error que en cuatro años supone
0'9688671... días, Julio César dispuso que cada cuatro
años se aumentara la duración del año en un
día y de esta manera aparecieron los años bisiestos
y el calendario juliano.
Pero no se resolvió del todo el problema porque el error es
de 0'9688671... días y no 1 día. El papa Gregorio XIII
en el año 1582 dispuso suprimir 3 días cada 400
años, dejando de ser bisiestos los años que terminen en
dos ceros y el número de sus centenas no sea divisible por 4.
Para compensar los errores hasta entonces, se pasó el 4 de
octubre de 1582 al 15 del mismo mes. Este es el calendario gregoriano.
-
Arquímedes (287 a. J.C.) fue el sabio que en la
antigüedad más se ocupó del estudio de las
áreas y volúmenes de los cuerpos.
Suyas son las siguientes fórmulas:
Área de la esfera: ..................... 4 ¶ R2
Volumen del cono: .................... 1/3 ¶ R2 . h
Volumen de la esfera: .............. 4/3 ¶ R3
Volumen del cilindro: ................ ¶ R2 . h
Murió en el año 212 a. de J.C. atravesado por la
espada de un soldado romano en el saqueo de la ciudad de Siracusa.
-
Los cinco poliedros regulares se conocían en el
siglo VI a. J.C. por Pitágoras y sus discípulos. Para
ellos tenían un sentido simbólico: el tetraedro
representaba el fuego; el cubo, la Tierra; el octaedro,
el aire; el icosaedro, el agua y el dodecaedro,
el universo en su integridad.
- Paolo Ruffini, matemático italiano (1765-1822)
publicó su famosa regla en 1804. Esencialmente coincide con la
publicada en 1819 por el inglés W.G. Horner. Antecedentes de
esta regla se han encontrado en trabajos de matemáticos chinos
en el siglo XIII.