Tú aprendes Matemática
Queremos darle una calurosa recepción a nuestra primera morada en este hiperespacio.
Como recién llegados nos disculpamos de las pocas atenciones que podamos brindarles, pero prometemos hacer todo el esfuerzo para en el futuro atenderle como se merece.
Le pedimos la mayor sinceridad y cooperación para poder alcanzar lo prometido, si Ud. nos ayuda seguro lo lograremos.
Sus sugerencias serán tomadas en cuenta y no olvidaremos agradecérselo públicamente.
Recuerde eso si, que está llegando a una casa que comienza a equiparse, y esto ocupa toda la vida en lograrse, pero cada día esperamos sentirnos mejor en ella, reiteramos que deseamos contar con su ayuda.
Cuando uno se está iniciando, la más pequeña colaboración es bien recibida, no tema darnos aunque sea ese granito de arena, el que con toda seguridad Ud. dispone. Sea solidario.
Por el momento estamos recibiendo su aporte en:
No deje de escribirnos.
Para saber de nuestras necesidades al respecto, le pedimos por favor, siga leyendo
nuestro proyecto.
Este es un proyecto en el cual el grupo comprometido con él, desea elaborar una serie de softwares orientados al aprendizaje de contenidos Matemáticos, pero con programas interactivos.
Está dirigido a una población, no estrictamente en un nivel escolar determinado. Los diferentes títulos de los contenidos, indicarán quién puede hacer uso de ellos. Es posible que no sean autosuficiente en los objetivos que pretenden lograr, pero fundamentalmente se espera que sirvan al docente como recurso.
En ellos se desea que los usuarios tengan la oportunidad de descubrir las relaciones matemáticas, que conllevan a las definiciones tradicionales.
Se espera que los conceptos aparezcan con
significado, producto de las diferentes experiencias a las que serán expuestos los
participantes.
El orígen de este proyecto tiene varias vertientes.
Algunas de ellas se exponen a continuación:
Es difícil delimitar el marco pedagógico del presente proyecto.
Son muchos los autores que podrían citarse, cada uno con una voluminosa producción.
Esbozaremos algunas ideas directrices, en
base a párrafos extraídos de obras de algunos exponentes que creemos dan
soporte a este trabajo.
Además daremos la opción de leer los siguientes artículos un poco más extensos,
que nos parecen pertinentes.
*Ciudadanía y educación matemática.
Eduardo Sebastiani Ferreira
*El método genético en la Psicología del
estudio del Pensamiento
Piaget
Ciudadanía y educación matemática.
¨Sin duda, es la matemática la disciplina que es la más llamada en la hora de arbitrar para la ciudadanía. Es ella quién más reprueba y por tanto es la gran responsable por la exclusión de la mayoría de la población de participar de la ciudadanía. Todo proceso selectivo, algunos necesarios, otros no, que la sociedad se ve obligada a emplear, cuando se tiene más competidores de lo que se necesita o capacidad de absorción, es la matemática solicitada a colocar el demarcador. Podemos entonces decir que cuando se habla de "vinculación entre ciudadanía y educación marcada por la exclusividad" es la Matemática la gran responsable. Más, ¿qué Matemática? En el artículo "Filosofía Antigua" de Lygia A. Watanabe del libro Primera Filosofía -Lecciones introductorias. la autora nos relata un poco de esa matemática-" ...Escuelas-científicas -filosóficas como la pitagórica, de la cual se guardó solamente la contribución purificada, matemática, no-mística, aislando así, el lenguaje matemático de su eficacia casi mágica. Esto sólo contribuyó para, en el correr de los siglos, mistificarnos a la matemática en sí misma, elevando el grado de 'mathesis universales'- especie de panacea epistemológica- imagen de que hasta hoy ella tiene dificultades para desembarazarse.
No fue solamente esa imagen de misticismo en sí mismo que la 'mathesis universales' vistió. Ella también incorporó la imagen de apolítica, la historia, verdad absoluta y otros adjetivos que sirven mucho para que una elite la use en el sentido, descrito encima, de demarcador del status de ciudadanía. La escuela fue y es una reproductora de ese status en el sentido de colaborar como precondición a la ciudadanía. "Aunque bien que el pueblo común tiene otras escuelas, donde aprende a ser sujeto de derechos y a luchar por ellos, sin dejar de lado las ciudades, las fábricas y las complejas empresas modernas", como escribió Arroyo.
Es entonces en esas "escuelas",diferentes de la escuela institucional que se da "el proceso interno de la práctica social y política de las clases" y es donde nace de hecho la ciudadanía. Es en ellas que debemos encontrar el conocimiento que debería dar el status de ciudadano. En cuanto estuviéramos esperando de la educación y en particular de la matemática, el gran "milagro de configurar el nuevo hombre libre para el nuevo mercado económico, social y político; en cuanto no estuvieren todos aptos para entender los valores de la nueva orden , en cuanto no estuvieren constituidos ciudadanos por obra y gracia de la educación, una minoría sabia, insigne, moderna y racional gobernará y decidirá por todos y para el bien de todos".
Este tipo de educación y principalmente de educación matemática decidida por una "elite sabia, insigne y racional" hoy ya no satisface los anhelos de la sociedad y es por esos motivos que esa sociedad insigne con sus status diferente del establecido, solicita algo más de la escuela que tenemos.
"El problema surge solamente cuando se piensa en la
enseñanza de la matemática de forma diferente. Si la concepción de la matemática como
un cuerpo de conocimientos cede lugar a la matemática como una actividad humana, la
matemática como proceso -en contraste con la matemática como producto- y, por lo tanto,
falible. Si no se permite que el alumno acepte 'verdades' sino por autoridad (sea del
profesor, del libro, etc.), en vez de que se fomente una actitud crítica en que cualquier
'verdad' es siempre verificada por el propio alumno. Si se encara al profesor como alguien
que hace matemática y no como el que detenta una serie de conocimientos estáticos. Si el
alumno es llevado a recrear la matemática, basándose en su intuición y lógica,
llegando a diferentes niveles de abstracción y de rigor, conforme con su propio
desarrollo y las necesidades por ellos sentidas. Esas son las premisas hoy pretendidas por
casi todo educador matemático preocupado por la ciudadanía del estudiante como bien
escribió Neeleman.¨
Extraído de traducción de artículo de Eduardo Sebastiani Ferreira
en "A educaçao matemática Nº1"
El método genético en el estudio de la psicología del pensamiento.
¨Desde el punto de vista del desarrollo, lo esencial del acto de pensar no es la contemplación -es decir, lo que los griegos llamaron "theorema"- sino la acción de la dinámica
Teniendo en consideración todo lo que se sabe, podemos distinguir dos aspectos principales:
1. El punto de vista formal que trata de la configuración del estado de
las cosas con el fin de conocer, p. ej., la mayoría de las percepciones, las imágenes
mentales y las de la imaginación.
2. El aspecto -dinámico-, que trata de las transformaciones, p. ej., desconectar un motor a fin de comprender su funcionamiento, separar y variar los componentes de un fenómeno físico para comprender sus causas, aislar los elementos de una figura geométrica para investigar sus propiedades, etc.
El estudio del desarrollo del pensamiento muestra que el aspecto dinámico es al mismo tiempo más difícil de alcanzar y más importante, porque sólo las transformaciones nos hacen comprender el estado de las cosas. -P. ej., cuando un niño de 4 o 6 años hace pasar un líquido de un vaso ancho y bajo a otro estrecho y más alto, cree, en general, que la cantidad de líquido ha aumentado, porque se limita a comparar el estado inicial (nivel bajo) con el estado final (nivel alto), sin preocuparse de la transformación operada. Por otra parte, hacia los 7 y 8 años, un niño descubre la conservación del líquido, porque ya piensa en términos de la transformación. Dirá que no se ha añadido nada ni se ha quitado nada y que si se eleva el nivel del líquido ello es debido a la pérdida de anchura, etc.-
Por consiguiente, el aspecto formal del pensamiento se abre paso cada vez más en el transcurso del desarrollo hacia sus aspectos dinámicos, hasta el momento en que sólo la transformación nos hace comprender las cosas. Pensar significa, ante todo, comprender; y comprender significa llegar a las transformaciones, las cuales nos suministran la razón del estado de las cosas. Todo el desarrollo del pensamiento se resume de la siguiente manera: una construcción de operaciones que brota de acciones y una subordinación gradual de los aspectos formales a los aspectos dinámicos.
La operación, propiamente hablando, que constituye el punto terminal de esta evolución debe concebirse, por consiguiente, como una acción interna reversible (p. ej., suma y resta, etc.) unida a otras operaciones, que forman con ella un conjunto estructurado y que se caracteriza por unas leyes bien definidas de totalidad (los conjuntos y los grupos, p. ej.). Las totalidades dinámicas son claramente distintas de la Gestalt porque aquéllas se caracterizan por su composición no aditiva y, por ello, irreversible.
Definida así, la dinámica interviene en la construcción de todos los procesos del pensamiento; en la estructura de las formas y clasificaciones, de las relaciones y la serialización de correspondencia, de los números, del espacio y tiempo, de la causalidad, etc. Se podría pensar, a primera vista, que el espacio y la geometría aumentan los aspectos formales del pensamiento. De esta manera se concebía la ciencia geométrica en el pasado, considerándola como una matemática impura, pero que era aplicable a la percepción y a la intuición.
La geometría moderna, desde la obra Le Programme d'Erlangen, de F. Klein, ha tendido, como otras disciplinas precisas, a subordinar lo formal a lo dinámico. La geometría se entiende hoy, en verdad, como un elemento de unión de todos los grupos de transformación, de suerte que podemos ir de uno a otro caracterizando un "subgrupo" menos general como parte de un grupo más amplio. De esta manera, la geometría también descansa en un sistema de la dinámica.
¨Cualquier acción de pensamiento
consiste en combinar las operaciones del pensamiento e integrar los
objetos que se han de entender en sistemas de transformación dinámica.¨
JEAN PIAGET
EXTRAíDO DE
"PSICOLOGIA DE LA EDUCACION" DE ANASTASI ET AL.
El decálogo didáctico de Puig Adam.
¨I. Adaptación No adoptar una didáctica rígida, sino amoldable en cada caso al alumno, observándole constantemente.
II. Genetismo No olvidar el orígen concreto de la Matemática ni los procesos históricos de su evolución.
III. Vitalismo Presentar la Matemática como una unidad en relación con la vida natural y social
IV. Gradación Graduar cuidadosamente los planos de abstracción.
V. Heurísmo Enseñar guiando la actividad creadora y descubridora del alumno.
VI. Interés Estimular dicha actividad despertando interés directo y funcional hacia el objeto del conocimiento.
VII.Autocrítica Promover en todo lo posible la autocorrección.
VIII.Maestría Conseguir cierta maestría en las soluciones antes de automatizarlas.
IX. Expresión Cuidar que la expresión del alumno sea traducción fiel de su pensamiento.
X. Exito Procurar a todo alumno éxitos que eviten su desaliento.¨
(Extraído de "Perspectiva histórica de las reformas de los currículos de Matemáticas de Gonzálo Sánchez" en Epsilon Nº 26)
Objetivos:
Nuestro proyecto se inició considerando sólo el primer
objetivo.
En relación a él, se han elaborado 3 CD y estamos recién esbozando el cuarto.
Con respecto a la evaluación en la ciudad de Maturín y alrededores, esperamos contar con la participación de profesores de esta zona, para evaluar los softwares, en grupos de la educación sistemática, tanto como en otros informales.
Al lograr este sitio en el espacio, nos pusimos
más ambiciosos y pensamos en la colaboración de las personas que nos
visitan, para tener una visión ampliada de lo logrado.
Para saber como colaborar diríjase a Evaluación.
El objetivo acerca de diseño de pautas que pudieran aplicarse a la
mayoría de los softwares que queramos evaluar, surge de la necesidad de hacer una para
estos en particular y previendo la evaluación de los próximos que se elaborarán.
Consideramos una prioridad llegar a un acuerdo para poder establecer la calidad de
los softwares.
Hay una persona dentro de nuestro grupo quién está interesada en un trabajo como este y
será la responsable de dirigirlo.
Pensamos que para realizar esta tarea también podemos contar con nuestros amigos en Internet, como colaboradores. Para enviar sus ideas al respecto los esperamos en sylviad@telcel.net.ve
El quinto objetivo referente al intercambio de información es otro objetivo que nace al radicarnos en Geocities.
Solicitamos también en este aspecto una contribución de nuestros nuevos amigos, nosotros apenas hemos esbozado una bibliografía, unas listitas de softwares y sitios en Internet. Esperamos que Ud. nos ayude a aumentar esta información. No olvidaremos hacer público nuestro reconocimiento, al igual que a cualquiera otra contribución que Ud. nos ofrezca.
La evaluación de nuestro proyecto constituye en el presente nuestra principal preocupación.
Estamos conscientes que cualquier tarea de evaluación es díficil de realizar y más aún quedar satisfechos con sus resultados. En este caso tratándose de una experiencia totalmente nueva para nosotros, sin otras previas que tomar como base para cimentar nuestras reflexiones, nos asusta y sentimos la necesidad de solicitar ayuda.
Recuerden que tenemos en mente, evaluar el proyecto en dos instancias, dentro de la Comunidad que nos desenvolvemos y ambiciosamente con grupos foráneos. Quisiéramos tener información aunque fuera de una muestra pequeña de este último grupo, para poder obtener algunas conclusiones al respecto.
Para realizar esta última parte de la valoración de nuestro trabajo, su ayuda nos es fundamental.
Si desea participar, haga click en las opciones abajo presentadas de acuerdo al rubro elegido:
Deseo colaborar en la elaboración de un patrón para evaluar softwares.
Deseo colaborar en la evaluación de los softwares confeccionados.
En relación con este punto, pensamos que es posible que existan instrumentos que nosotros desconocemos, si Ud. sabe de algo al respecto, le agradeceríamos nos hiciese llegar dicha información.
No cabe duda que si decidiéramos usar un instrumento como aquel, indicaríamos su procedencia y si lo usamos como material de apoyo, se incluiría en la bibliografía utilizada, se procederá de igual modo si se trata de ideas particulares de la persona que está enviando su contribución.
En relación con este aspecto, es obvio que no disponemos de la pauta que estamos precisando. Pero si Ud. quisiera tener acceso al material elaborado, para hacerle observaciones, estaríamos muy agradecidos de su ayuda, en este caso además le pediríamos que en el futuro cuando dispongamos del instrumento que uniformará nuestros comentarios, Ud. acepte llenarlo.
Hasta el momento sólo disponemos de 3 CD elaborados:
-Parábola
-Elipse
-Cónicas, este último contiene, como es de suponer, buena parte
de los dos anteriores.
En esta primera etapa estaremos sólo enviando Parábola, ya avisaremos cuando empecemos a distribuir los otros.
Para recibir este CD , Ud. debe escribirnos a sylviad@telcel.net.ve adjuntando sus datos personales, dentro de los cuales nos gustaría conocer su profesión, trabajo actual y las razones de su interés.
Al responderles le estaremos solicitando el lugar dónde enviarlo, el valor de la copia del CD y de envío, todo a precio de costo, nos hubiera gustado poder regalarlo, pero somos unos modestos profesores.
Estamos optimistas, esperamos impacientes que nos dedique un poquito de su tiempo en una tarea que es posible beneficie a algunas personas.
El beneficio del colectivo es el que mueve nuestro interés.
En esta parte hemos querido incluir información sobre material recopilado por el grupo.
| Bibliografía | |
| Softwares | |
| Sitios en Internet |
La lista no es muy extensa, recién nos iniciamos, pero esperamos que la valiosa colaboración de nuestros visitantes, nos permita incrementarla.
Su contribución la esperamos en: sylviad@telcel.net.ve
Bibliografía sobre educación matemática
*En relación con toda la colección de Martín Gardner, está casi demás decirlo, es la que creemos debería estar en la biblioteca de todo profesor de Matemática.
Nosotros iremos entregando, en fechas futuras, un mayor número de títulos de este insigne y productivo autor.
Otro autor que pensamos no puede faltar en una lista como la que estamos presentando, es Zoltán Dienes, existe una voluminosa cantidad de títulos de este prestigioso Doctor en Psicología y Matemática, nos comprometemos, más adelante, a dar por lo menos parte de ella, la que tenemos disponible.
Estaremos muy agradecidos de recibir su aporte.
Para contribuir a incrementar esta lista escríbanos aquí sylviad@telcel.net.ve, sólo
solicitaremos que los juegos que se incluyan, cumplan con la siguiente característica,
que tengan el menor ingrediente de azar y sirvan para desarrollar formas de
pensamiento.
Bibliografía sobre
Historia de
la Matemática y biografía de matemáticos
Bell, E. T. Los grandes matemáticos Editorial Losada Bs. As 1948
Bourbaki,
Nicolas Elementos de Historia de la
Matemática Alianza Universidad
Madrid 1976
Bourbaki, N Théorie des Ensembles Hermann Paris 1970
Féliz, Lucienne Matemática Moderna Kapelusz Bs. As. 1968
Infield, Leopold El elegido de los Dioses Siglo XXI Bs. As. 1948
I.R.E.M. Epistemologie et histoire des Mathematiques I.R.E.M. Paris 1980
Kline, Morris Matemáticas en el mundo Moderno Editorial Blume Madrid 1974
Vera, Francisco
Breve Historia de
la Matemática
Editorial
Losada Bs. As. 1946
IDEAS DIRECTRICES
¨El fundamento más esencial y más próximo del pensamiento humano es,
precisamente, la transformación de la naturaleza por el hombre,
y no la naturaleza por sí sola, la naturaleza en cuanto tal.¨
Friedrich Engels
Dialéctica de la naturaleza
¨Al igual que las herramientas de trabajo cambian
históricamente, también las herramientas del pensamiento cambian históricamente. Y así
como las nuevas herramientas de trabajo dan lugar a nuevas estructuras sociales, también
las herramientas del pensamiento provocan el nacimiento de nuevas estructuras mentales
(........) uno se siente inclinado a considerar a la estructura de la mente
como algo universal y eterno, sin embargo tanto las estructuras sociales como
las estructuras mentales poseen raíces históricas bien definidas.¨
Lev S.Vygotsky
Theory
¨Mientras que los poderes del hombre son
expresados y amplificados por los instrumentos de la cultura, los límites que puede
alcanzar la riqueza del conocimiento individual seguramente sean tan amplios como las
combinaciones de las capacidades culturales.¨
Jerome S. Bruner
Investigaciones sobre el desarrollo cognoscitivo
"Es necesario transformar el énfasis en la enseñanza a
énfasis en el aprendizaje, de nuestra experiencia a la de los niños, en realidad de
nuestro mundo a su mundo".
Zoltán Dienes
¨El profesor medio aún con espíritu moderno, no puede tener las
perspectivas científicas accesibles a un investigador; él realiza las tendencias
modernas sobre un terreno restringido y limitado, puede facilmente -de buen grado o por
fuerza- reducir una idea metodológica creadora a detalles tratados de una manera
exagerada. Esto porque, en la base de todas nuestras marchas pedagógicas, necesitamos
poseer como un parapeto el siguiente principio: no debemos ser más ¨católicos que el
Papa¨, es decir más ¨puros¨ en nuestra enseñanza, que los matemáticos en su
práctica cotidiana habitual.¨
Z Krygowska
El problema del rigor
¨La matemática que nace en la misma forma que las otras disciplinas,
tiene, sin embargo, un carácter diferente, es, según se dice tan a menudo, más
ABSTRACTA, y lo es fundamentalmente porque la Matemática no se preocupa de objetos, sino
que de INTER-RELACIONES. Si tuviera que definir la Matemática en dos palabras diría que
es la Ciencia de las inter-relaciones. Inter-relaciones entre todo; no sólo entre objetos
del mundo natural, como ocurrió al comienzo, sino que también inter-relaciones en el
mundo concreto, CREADO por el hombre e inter-relaciones en el mundo de las ideas CREADAS
por el hombre.¨
Jaime Michelow
¨La Matemática y el Hombre¨
Pensamos que este programa al igual que Elipse, puede ser usado en varios
niveles, por supuesto seleccionando las opciones adecuadas.
Tal vez niños de los últimos años de primaria podrían adquirir una idea general acerca
de lo que es la Parábola. Es evidente que es para Secundaria donde estaría recomendado,
por constituir un contenido del programa.
Pero tal vez, y esto está en prueba, en la Universidad podría recomendarse como
actividad de nivelación.
Nuestro software Parábola fué diseñado para que los usuarios pudieran optar por una idea general acerca del tema o entrar a estudiar los detalles.
Dentro de la generalidades incluímos definiciones, algo de historia, algunas aplicaciones y gráficos de esta curva. Esta última parte es interactiva, el usuario cambia los parámetros para modificar el gráfico.
En el estudio detallado que llamamos Paso a Paso, puede elegirse entre obtener
la expresión analítica de la parábola y/o determinar que la gráfica de una función de
segundo grado corresponde a un parábola.
Esta parte del programa es totalmente interactiva, el usuario debiera lograr por la vía
inductiva y deductiva la comprensión del concepto.
Pensamos que este programa al igual que parábola, puede ser usado en varios
niveles, por supuesto seleccionando las opciones adecuadas.
Tal vez niños de los últimos años de primaria podrían adquirir una idea general acerca
de lo que es la elipse, está por evaluarse. Es evidente que está especialmente
recomendado para Secundaria, por constituir un contenido del programa.
Pero tal vez, y esto está, en este momento, siendo sometido a prueba, también en la
Universidad podría recomendarse como actividad de nivelación.
Este software al igual que Parábola tiene dos opciones para el usuario, elegir entre adquirir ideas generales sobre el tema y/o estudiarlo en sus detalles.
También al igual que en Parábola dentro de la generalidades incluímos definiciones, algo de historia y algunas aplicaciones.
En el estudio detallado que llamamos Paso a Paso, puede elegirse entre
identificar elipse y sus elementos y/o deducir la expresión analítica de la
elipse y/o demostrar la equivalencia entre algunas definiciones.
Esta parte del programa es totalmente interactiva, el usuario debiera lograr por la vía
inductiva y deductiva la comprensión de este nuevo concepto.
Pensamos que este programa al igual que los otros que hemos diseñado, tienen
la característica de poder ser usado en varios niveles, por supuesto seleccionando las
opciones adecuadas.
Sin embargo en este caso no estaríamos pensando en niños de primaria. Es evidente que
está especialmente recomendado para Secundaria, por corresponder a los
contenidos del programa.
Pero tal vez, y esto está, en este momento, siendo sometido a prueba, también en la
Universidad podría recomendarse como actividad de nivelación. No está pensado
para satisfacer los requerimientos de los programas de Enseñanza Superior.
Este software es el resultado de Parábola y Elipse juntos, más un
trabajo acerca de Hipérbola.
Por supuesto como era de esperarse las opciones en este caso son elegir alguna de las
Cónicas que se desee estudiar y a continuación en cada una de ellas, elegir entre
adquirir ideas generales sobre el tema y/o estudiarlo en sus detalles.
Cada uno de estos aspectos tienen nuevas posibilidades de elección que en los casos de Parábola y Elipse están anteriormente descritas en los programas separados.
En el caso de Hipèrbola al igual que en las anteriores dentro de la generalidades incluímos definiciones, algo de historia y algunas aplicaciones.
En el estudio detallado que llamamos Paso a Paso, puede elegirse entre
identificar hipérbola y sus elementos y/o deducir la expresión analítica de
la hipérbola y/o demostrar la equivalencia entre algunas definiciones.
Esta parte del programa es totalmente interactiva, el usuario debiera lograr por la vía
inductiva y deductiva la comprensión de este nuevo concepto.
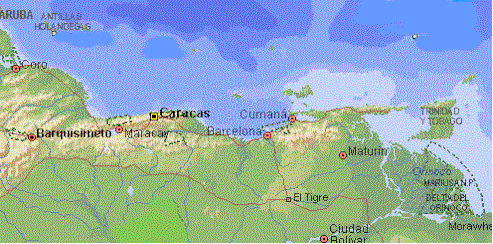
Es una hermosa ciudad de Venezuela que se encuentra a 500 kms. de Caracas en el Estado Monagas, en la zona Nor oriental del país.
En el mapa podemos apreciar su ubicación, se encuentra
más cerca de Trinidad Tobago que de Caracas.
Es llamada ¨una ciudad distinta¨ y hace honor a esta calificación
Cuenta con varios Institutos de Educación
Superior, como los núcleos de las siguientes Universidades:
Universidad Pedagógica Experimental Libertador (UPEL).
Universidad de Oriente (UDO).
Universidad Santa María.
Universidad Nacional Abierta (UNA).
Universidad Gran Mariscal de Ayacucho.
Universidad Simón Rodríguez.
También se encuentran núcleos de Institutos Tecnológicos:
Instituto Universitario Tecnológico de Venezuela (IUTV).
Instituto Universitario Politécnico Santiago Mariño (IPSM).
Instituto Universitario de Tecnología Industrial ¨Rodolfo Loero Arismendi (IUTIRLA) .
Regresar a objetivos Regresar a avance