
When I first found out about this project, the first thought that came into my mind was that it would be really interesting to research the lives of women in mathematics. The next thought that crossed my mind was that I had never really heard of many. After that I thought I had better choose another topic as there wouldn't be any information about this one. However, as I was looking for information on other potential topics, my eyes fell on a book called "Notable Women in Mathematics." Next to that book were several other books with similar titles. Excitedly I grabbed the books and checked them out.
As a young girl, I loved math. As a matter of fact, math has been my favourite subject throughout my schooling. That is why I want to become a high school math teacher, to share my love and fascination with numbers and hopefully inspire my students to develop a similar affection for the (much dreaded) subject. However, as I pursued my education in mathematics, I began to realize that I never really heard much about female mathematicians (except Hypatia). Traditionally, mathematics has been seen by the layman as a "mans" field, so as a girl interested in mathematics I wanted to know if this was true. I started to wonder what kinds of contributions women have made to mathematics. It is interesting to note that As early as the nineteen-seventies there were approximately equal numbers of men and women pursuing their bachelor’s degree in mathematics. In the pages that follow, I will illustrate the lives of three women in mathematics (all from different periods in time) and their contributions to the field. I have chosen Hypatia, Maria Agnesi, and Andrea Bertozzi because they have all made major contributions to mathematics during their lifetimes and because their personal stories interested me.

Hypatia (circa 360-415)
Hypatia is the first female mathematician who has been remembered throughout history. One might be led to wonder how Hypatia became interested in mathematics as in the era she was born into seriously discouraged women from taking an interest in academics; education was seen as a rich man’s domain. Hypatia was the daughter of a man called Theon who wanted to raise the "perfect" child. He envisioned his child as being physically fit, and being skilled in the arts as well as the sciences. For some peculiar reason, as this did not fit with the thinking at the time, it did not descourage Theon in the least that his child was a girl. Thus Hypatia was raised with the idea that physical fitness together with artistic ability and scientific expertise were the essentials of a happy life. As far as Theon would be concerned, his experiment was a success. As a matter of fact, Hypatia surpassed her father in mathematical ability and knowledge and had to be sent to Athens to study. She later travelled across Europe. Hypatia was a very beautiful woman and was asked several times for her hand in marriage but she always declined the offer because, at the time, it would mean leaving her mathematical career and so great was her love and devotion to mathematics.
After her travels in Europe she got a teaching position at the Universiy of Alexandria. The university at Alexandria was established by Ptolemy as the first university in the modern sense. The experience of teaching there was something Hypatia shared with Euclid who was the head of the mathematics department some seven hundred years before Hypatia was even born. People came from all over the world to hear Hypatia lecture and because of her intellectual brilliance she was seen as a goddess or an oracle, or something along those lines. When the Romans attempted to conquer all of Greece, mathematics was strongly discouraged and Hypatia was one of the last teachers to attempt to defy the Romans.
Unfortunately for Hypatia, her defiant spirit led to her death. As a Neoplatonist she did not want to accept the doctrines of the early Christian church. Because she was such a prominent woman, Cyril, the patriarch of Alexandria, was afraid that she had enough influence over the general population of Greece that she could actually hinder the growth of Christianity. That is why he started the rumour that all religious leaders would be able to work together if Hypatia were killed. He was taken seriously and in 415 Hypatia was lynched by a crowd in a Church(which is obviously a very un-Christian act) after being pulled out of her chariot by the hair and dragged through the streets. Cyril must have taken pleasure in the fact that Hypatia’s death saw the end of mathematical studies in Alexandria for an entire millenium.
As a teacher, Hypatia taught geometry and astronomy although her real interest was in algebra. As an author, Hypatia wrote commentaries on Diophantus and Euclid as well as a book called Atronomical Cannon of Diophantus and Conics of Appolonius. Actually, she probably wrote much more than these books but as printing had not been invented yet there were few copies of books if any at all, as such, much of what was written during this period is lost. In fact, we owe much of our knowledge of Hypatia’s work to letters she wrote to her pupil, Synesius of Cyrene. As an inventor she is credited with several ingenious processes and devices. Among them are a process for distilling sea water that has continued to be useful to us today, the astrolabe(a device that measures the positions of stars and planets), and the hydroscope(a device that allows you to see objects deep underwater).
As a mathematician, Hypatia looked mostly at the importance of conic sections. Her book, Atronomical Cannon of Diophantus and Conics of Appolonius consisted of treatises and conic sections. Her work on conics was based on the work of Apollonius (as the title suggests) who worked in Alexandria five hundred years before Hypatia. Years after her death, Hypatia’s work proved very useful as many natural phenomena are described by the curves she investigated. Her work also influenced Descartes, Newton, and Leibniz.

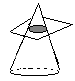
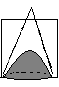
The
conic sections that hypatia worked with were ellipses, parabolas, and a
hyperbola. She constructed these by passing a plane through a cone. Here
are a couple of examles of how she constructed these curves. The first
is an ellipse, the second a circle and the third a hyperbola.

Maria Gaetanta Agnesi (1718-1799)
By the eighteenth century, society had progressed enough to see education as something appropriate for rich women; the poor were still highly uneducated. Although it was seen as acceptable for rich women to be educated it was still uncommon as it was not considered necessary for women to be knowledgeable about anything other than social graces and dressmaking, and we find that Maria’s story is similar to that of Hypatia.
Maria was born in Italy to a rich and scholarly family. Maria’s father realised that she had a good memory while she was still quite young and he took advantage of this by having her and her sister perform recitals in which they played music, read speeches and conducted mathematical debates for their guests in latin(the language used by educated people at the time). In the same way as Theon, Maria’s mathematician father moulded the "perfect daughter" as a sort of experiment. Unlike Hypatia, this was not necessarily a role that Maria wanted to play as she was shy but while she was young she did it nonetheless to please her father.
After her mother died, fourteen year old Maria was left to take care of her family which, after her father’s two remarriages, consisted of 20 children (excluding herself). During this time she continued to perform the aforementioned recitals as well as study math and science with several tutors. Eventually, her studies combined with the work of taking care of her family became too much for her and she began to have seizures. Her seisures were probably made worse by her doctor’s prescription of horseback riding and dancing! After pleading she pleaded with him, her father let hr out of the debates and let her go to a convent for some rest athough he would not allow her to become a nun. She continued working on mathematics mostly because she was teaching her younger siblings.
The one thing that really dealt a blow to Maria’s career was the death of her father in 1752. Despite all of the problems that could have occurred in their relationship from the way he expected these performances from her at a young age to her father’s remarriages, they had been very close until the day he died. Because it had been her father encouraging her all along to persue mathematics, she gradually pulled herself away from her mathematical career because it reminded her too much of her late father.
Before Maria’s mathematical career ended she published some very interesting things that came out of her personal. The debates that she conducted at her father’s parties provided Maria with the opportunity to make logical arguments for almost two hundred topics. Those topics included anything from math, to scince, to philosopy. She put all two hundred of these topics into her book called Philosophical Propositions. An example of a typical debate topic is the ancient celestial-mechanics vs. universal gravitation. Also from the recitals she performed as a youth, Maria published her speech on why women should be educated.
Another book she wrote drew its origins from tutoring sessions with her brother in which she began to look at Leibniz, Newton, Kepler, Galileo, and L’Hopital in a way that no one ever had before. She translated their work into Italien so that people who only spoke Italien would have acess to them as well. It is probably the greatest work she produced and it was called the book Analytical Institutions. This book was very widely known and used in mathematical circles. In fact Rev. John Colson (Cambridge university) learned Italian for the sole purpose of translating it. The book was essentially a textbook about algebra and analysis that used the calculus of Leibniz and Newton. It got her so much regognition that the Empress and the Pope bestowed jewelled treaures on her. The book’s success was considered by many a huge step toward the acceptance of women as productive and intellectual beings. The education of women was Maria’s favourite cause. The following quote is from the dedication of the book to the Empress, Maria Teresa:
…none has encouraged me so much as the consideration on your sex, to which You Majesty is so great an ornament, and which by good fortune, happens to be mine also. It is this consideration chiefly tht has supported me in all my labours, and made me insensible to the danges that attended so hardy an enterprise… Indeed I am fully convinced, that in this age, an age which, from your reigh, will be distinguished to latest posterity, every Woman ought to exert herself, and endeavour to promote the glory of her sex, and to contribute her utmost to increase that lustre…
Ironically, through one of the seemingly common glitches in the annals of mathematics, Agnesi is most remebered for something that she did not discover, the Witch of Agnesi. Not only was the curve actually discovered by Fermat one hundred years earlier but the word "witch" is a mistranslation of the word versiera (curve in English). The mislabelling occurred because Agnesi did some work on the curve even though she did not discover it. The witch can be generated by starting with a circle and a line and trying to find points which are on the curve.
Later in her life, after she had totally abandoned her mathematical career, she moved into a small home and took in some poor people. To pay the bills she taught catchism. Unfortunatley that did not give her enough money and she had to sell the ring and crystal jewelry box that were laden with diamonds, and other priceless items that the Empress of Austria and the Pope in honour of Maria’s mathematical expertise. Perhaps it was a final symbol of her letting go of her mathematical career. At any rate, she went on to become the director of a home for the sick and aged called Pio Albergo Trivulizo. She died pennyless in 1799 at the extraordinary (for the time) age of 81.

Andrea Bertozzi (1965- )
Andrea Bertozzi has something in common with Hypatia and Agnesi, her father is also a mathematician. She was born in Massachusetts in 1965. From a young age Andrea loved mathematics. In fact most of her childhood memories revolve around mathematics. "I didn't enjoy doing exercises," she said. "It was more the concepts. Most of us who go into the field don't like the memorizing."
The fact that she was put into an advanced class with only male students at the age of eleven helped Andrea to learn how to work on her own and solve problems because the boys would all work together and exclude her.
Andrea went to Princeton University and finished her bachelor’s degree in 1987, her master’s in 1988 and her Ph.D. in 1991 in mathematics. She then received an NSF Postdoctoral Fellowship at the University of Chicago. This is where she became interested in what she is currently investigating: the behaviours of film surfaces. This may sound more like physics than mathematics but what Andrea has an interest in is the area where abstract mathematics and applied physics meet. I went to Andrea’s website to read about her research so that I could discuss some of the mathematics involved but I did not understand any of it as it was way beyond any math I have ever taken.
As far as being a woman in the field of mathematics, Andrea says, "It's all a perception thing. I think it will change slowly." She is really happy at Duke University and she feels surprisingly welcome there, "They're supportive of my research. I do not feel singled out here. I'm really treated as one of the gang. I like that. I don't like separate but equal, and I didn't want to be a token."
In conclusion, although mathematics has traditionally been seen as a "man's" field, women have been active in mathematics for centuries and continue to be so. It might be possible for someone to criticize the centuries in which it was considered inappropriate for women to work or even educate themselves and thus the apparent lack of female mathematicians; but why dwell on the past. Let us look to the present where women have as great a chance at realizing their goals; even as future mathematicians, should they so choose.
References: