Instituto Oriente

Matemáticas III, Examen Unidad II

1. Escribe la respuesta en la forma a + bi.

Solución:

a)

b) (4 + i)[i - 3 + 10 - 6i] = (4 + i)[7 - 5i] = 28 - 20i + 7i + 5 = 33 - 13i

2. Escribe la respuesta en la forma a + bi:

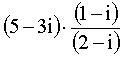
Solución:

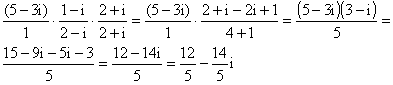
3. Encuentra la potencia indicada del siguiente número complejo:

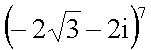
Solución:

Obtenemos los valores de r y q :

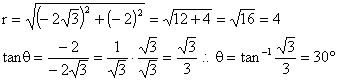
Como este número se encuentra en el tercer cuadrante, el ángulo real se obtiene al sumarle a 180º los 30º que encontramos originalmente, lo que nos da 210º.

Para encontrar la potencia:

r = 4⁷ = 16,384 y q = 210º * 7 = 1470º

de aquí: 16,384(cos 1470º + i sen 1470º) = 14,188.96 + 8,192 i

4. Encuentra la raíz cuadrada del siguiente número complejo:

Solución:

Planteamos el siguiente sistema de ecuaciones no lineal.

Despejamos y de la ecuación 2 y simplificamos: y = 20/x

Substituimos en la ecuación 1: x² - (20/x)² = -9

Simplificando: x⁴ + 9x² - 400 = 0

Realizando un cambio de variable: U = x²

La ecuación nos queda: U² + 9U - 400 = 0

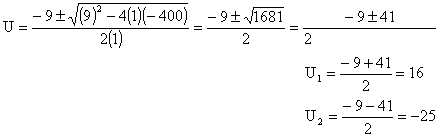
Descartamos la solución negativa y tomamos la positiva U = 16

de aquí obtenemos que x² = 16 entonces x₁ = 4 y x₂ = -4

Substituyendo estos valores en el despeje de la ecuación 2 tenemos entonces

y₁ = 5 y y₂ = -5 de aquí encontramos los números buscados:

4 + 5i

4 - 5i

5. Busca el valor de x y y en: i² (1 - i)(1 + i) = 3x + yi + i(y + xi)

Solución:

Desarrollando el miembro derecho e izquierdo tenemos

(-1)(1² - i²) = 3x + yi + yi + xi²

(-1)(1 + 1) = 3x + 2yi - x

- 2 = 2x + 2yi

Igualando la parte real de la izquierda a la de la derecha:

- 2 = 2x de aquí x = -1

Igualando la parte imaginaria de la izquierda a la de la derecha:

0 = 2 y de aquí y = 0

6. Una de las aplicaciones de los números complejos en la Teoría de Circuitos. Cuando dos impedancias x y y son conectadas en paralelo, la impedancia z del circuito está dada por:

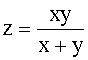
Escribe z en la forma a + bi sí: x = 5 - 3i ; y = 2 + i

Solución:

Substituimos el valor de x y y en el valor de la impedancia: