Para las personas que tienen que entregar proyecto final el día del Examen final. del 13 de Diciembre del 2002

Por grupos:

5ºB.- Arellano Olvera Jorge

5ºC.- Gómez Rayón Fernando

5ºD.- Ostrovskaya Yekaterina, Torres Nava Rosa Del Carmen, Robles Salmerón Adriana

5ºE.- Amuchástegui Reynoso Iñaqui, Díaz Hernández Hector A. Mastretta Real Aldo

SOLO estas personas deben de entregar su proyecto final, el cuál consiste en lo siguiente:

1) Estudiar del capitulo X del Lehman que empieza en la página 237 del mismo lo relativo a coordenadas polares, el paso de coordenadas polares a rectangulares y viceversa (pág. 239) discutir el Teorema I de esta misma sección.

2) Trazado de curvas en coordenadas polares (pág. 244), comprender los seis pasos descritos para construir curvas en coordenadas polares. Teorema 2 (Pág 245), revisar los ejemplos 1 y 2 (página 246 y 247)

3) Realizar el trazo en papel polar a "mano" (sin computadora) de las siguientes ecuaciones polares (tienes el resultado de la gráfica para que te guíes de él, no para que lo copies sin razonarlo)

Ejercicios: 2, 6, 10, 14, 19, 24, 26, 29, 33, 34. del Proyecto final de Otoño del 99, que se encuentra abajo...

4)En todo caso para cada una de estas curvas debes de seguir los 6 pasos descritos en la página 244 y expresarlos por escrito.

5) Entregar en un folder las graficas con sus pasos cada una, además debes de dar 2 ejemplos de APLICACIÓN de las coordenadas polares.

Proyecto final de Otoño del 99 (solución)

Traza la gráfica de las siguientes ecuaciones polares.

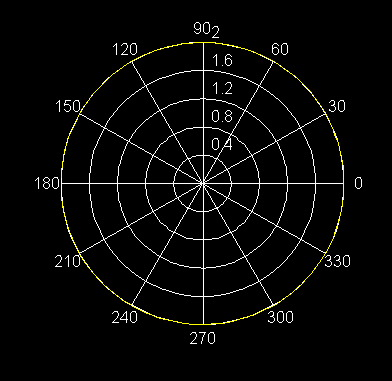
2) r = -2 Círculo con su centro en el origen y de radio igual a 2

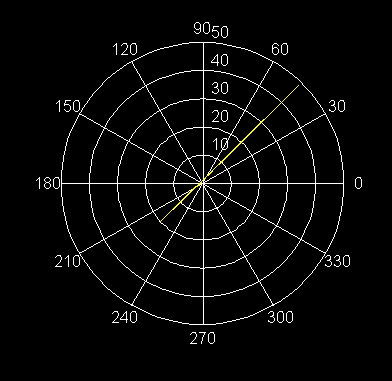
4) q = p /4, Línea recta que pasa por el origen, a 45º

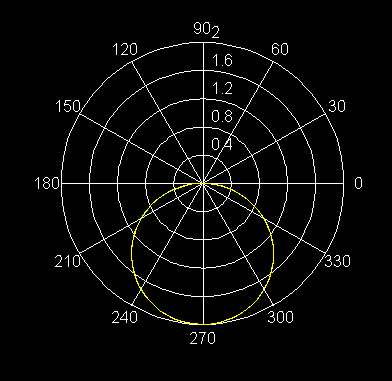
6) r = -2 sen q

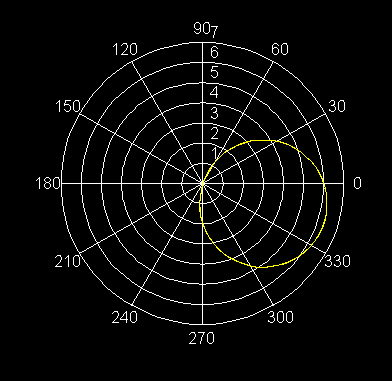
8) r = 6 cos q - 2 sen q

10) r = 3(1 + cos q ) Cardioide

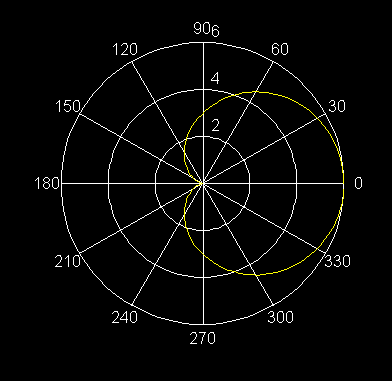
12) r = 2(1 + sen q ) Cardioide

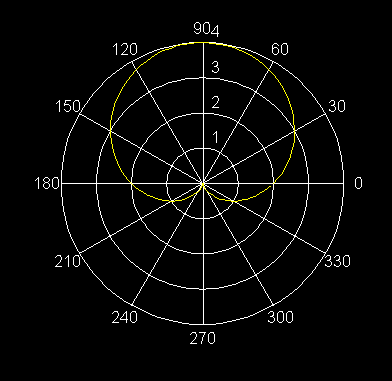
14) r = 1 + 2 cos q Caracol con lazo interior

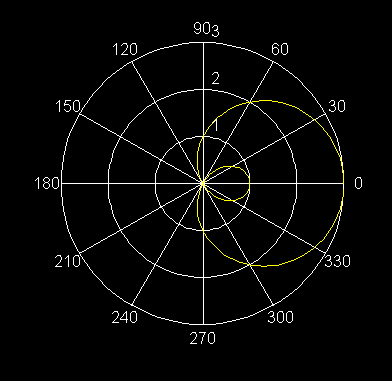
16) r = - 4 cos q Caracol con lazo interior

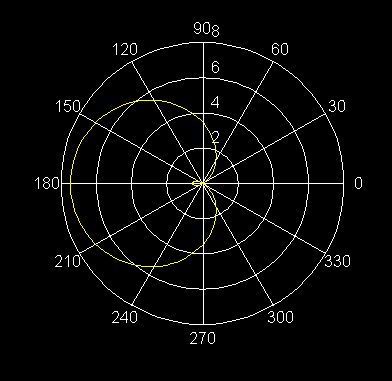
18) r = 5 + 3 sen q Caracol convexo

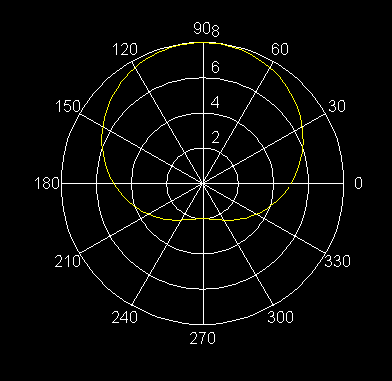
20) r = -3 sec q Equivale a la recta x = -3

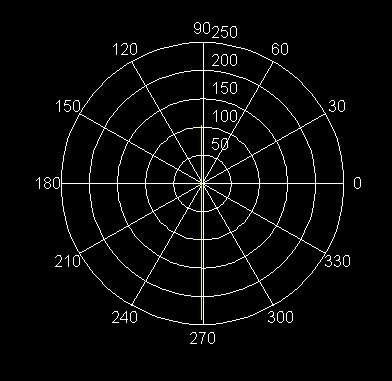
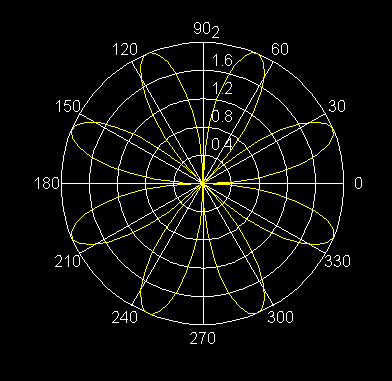
22) r = 2 sen 4q Rosa de 8 pétalos

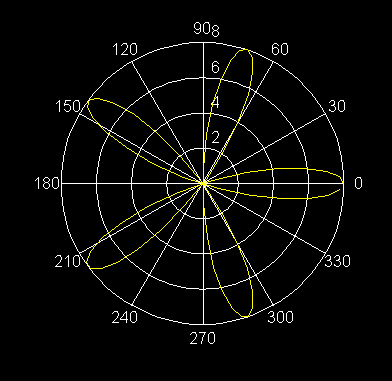
24) r = 8 cos 5q Rosa de 5 pétalos

25) r² = 4 cos 2q Lemniscata

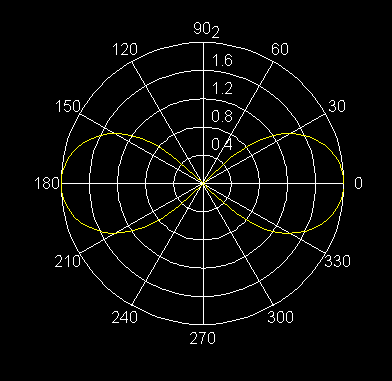
26) r² = -16 sen 2q Lemniscata

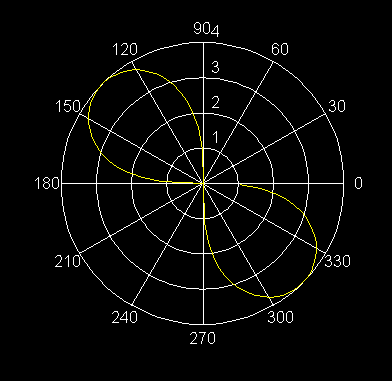
27) r = 2q , q ³ 0 Espiral

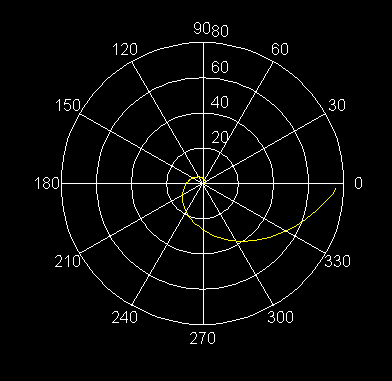
28) r = e^2q , q ³ 0 Espiral exponencial

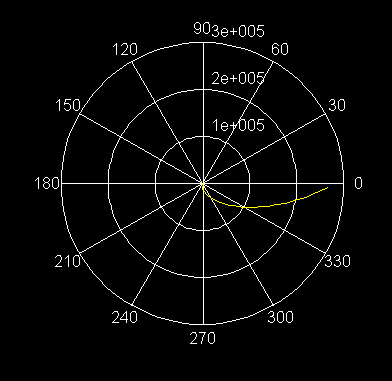
29) r = 2q , q ³ 0 Espiral de Arquímides

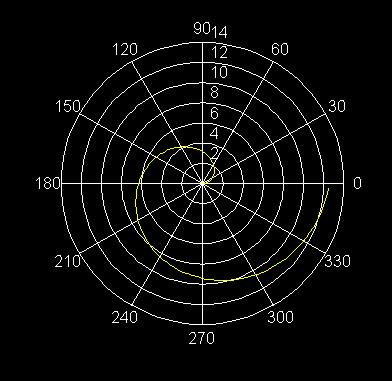
30) rq = 1, q > 0

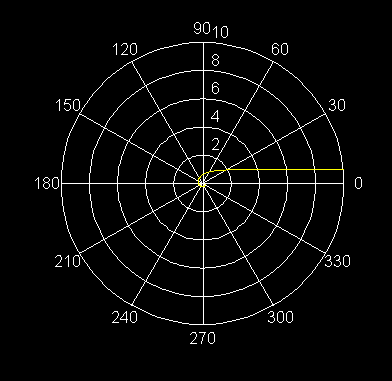
31) r = 6 sen ² (q /2)

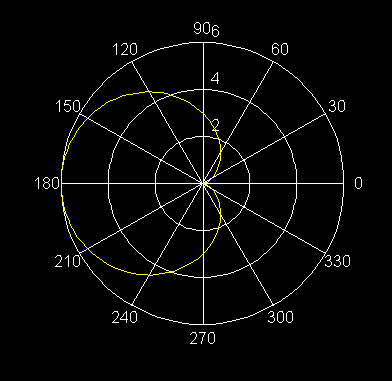
32) r = -4 cos²(q /2)

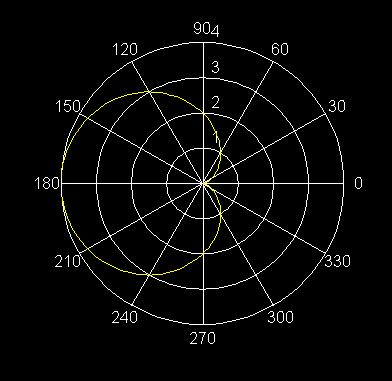
33) r = 2 + 2 sec q Concorde

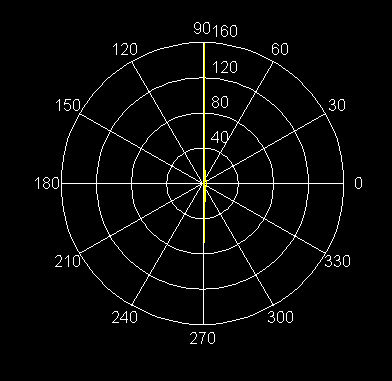
34) r = 1 - csc q Concorde

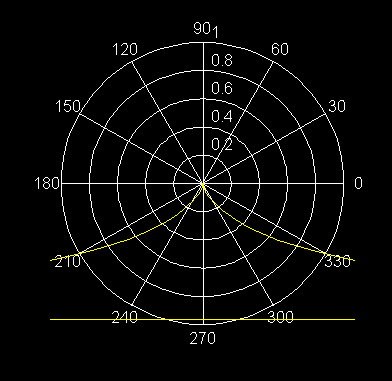
 36) x = -4.33; y = 2.5

38) x = 2.83; y = -2.83

 47) r = - 3 secq

49) r = 4

51) q = tan ^-1 (-1/2)

53) r² = -4 secq

55) r = 2 cosq

57) x = 5

59) x² + (y - 3)² = 9

61) y = x

63) (y² / 9) - (x² / 4) = 1

65) x² - y² = 1

67) y - 2x = 6

69) y = - x² + 1

71) (x + 1)² + (y - 4)² = 17

73) y² = x⁴ / (1 - x²)

Página principal ½ Página Anterior