Calculating Pi

Calculus:

Geometric:

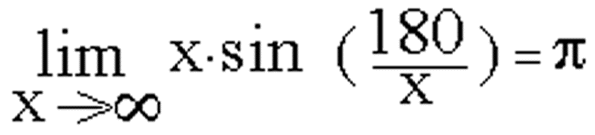
The following is how I derived this formula. To start with, the problem should be made much more simple.
Pi is the ratio of the circumference of a circle to the diameter. We can look at a circle as, not a figure with a curve, but a geometric figure with infinite angles. To simplify it further, we make it even less of a circle, giving in less and less angles and sides. Sooner or later (later) we will wind up with a shape like a octagon or hexagon. We can much more directly find the measure of both the circumference and diameters here. There are all sorts of useful relationships. If we draw lines from each corner to the corner exactly opposite it, we get something which resembles the diameter of a circle. We also get a number of triangles(x) that are all the same. This only works if the object has an even number of sides, so that these triangles actually are the same. The smallest angle of these triangles (which was once the one attached to the center of the figure) is equal to 360 degrees divided by the number of sides on the object(x). Both of the other two angles on the triangle can be found fairly easily since they are both the same, and the three angles of a triangle always add up to 180 degrees. Going back to the circle, we find we want the distance around the object divided by the distance through. If one point of the triangle used to be at the center of the triangle, then the longer sides of these triangles are equal to half the diameter. To simplify further, we will force the distance around the object to be Pi by making the diameter of the object one. This makes the length of the long side of each triangle one half. By using the Sine Law* we can find a relationship for a regular object with any number of sides. And, moving outwardly from our simplicity, we would find that as the number of sides approaches infinity, our calculation of Pi becomes closer and closer.

*note - The Sine Law is; the sine of any angle within a triangle divided by the length of it's opposing side is equal to the same relationship with any other angle in that triangle.