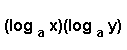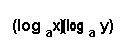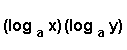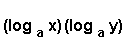INDICES AND LOGARITHMS (INDEKS DAN
LOGARITMA)
III. Addition/Subtraction and Multiplication/Division
The tables are divided this way:
- LEFT: Numbers in Logarithm Form (Bentuk logaritma)
- RIGHT: Numbers in Index Form (Bentuk Indeks)
- TOP: Things you are allowed
to do
- BOTTOM: Things you are not
allowed to do
The rules in the grey area are not "true"
index/log laws, but can be used here nonetheless.
Note: Base (English) = Asas (Malay)
|
ADDITION/SUBTRACTION |
|
2 logs of the same
base can be combined.
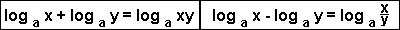

|
Different numbers can only be
combined
by factorizing.
a2 - b2 = (a
+ b)(a - b)
Aside from
factorizing, the only other possible way to combine index-forms is when they
are EXACTLY the same
am +
am
= 2am
|
|
2 logs of different
bases must be left
alone.
log
a
x + log b y
log a x + log
b x
|
Numbers with
the same base but different
index must be left alone. (except
when Factorizing)
a5
+ a3 - a2
am + an
(The best example is our Good Friend the
Quadratic Equation)
x2 + x1
Non-logs with
the same index but different
bases must be left alone. (except
when Factorizing)
a2
+ b2 + c2
xm - ym
- zm
|
|
MULTIPLICATION/DIVISION |
|
When dividing
logs of the same base, they can be combined.
(This involves Changing Bases, which is not in the West Australian TEE
syllabus) 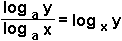
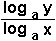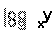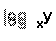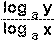
|
Same
base, different index:
am x
an = am+n
am ÷
an = am-n
Same index,
different base:
Compare these with the beginning of the previous
page
xa *
ya
= (x * y)a
xa ÷ ya =
(x ÷ y)a
|
| NO Logarithms can mix when being multiplied.
Leave them alone.
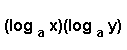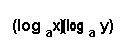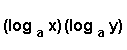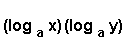
Logarithms of different
bases also do
not mix when multiplied/divided.
Leave them alone.
|
Different
base, different index:
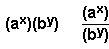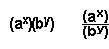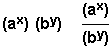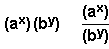
|
Extra
Ok, so we've established the rules for adding/subtracting
TWO logs. Now, what happens when you come across something like this?:
- log x a + log x
b - log x c + log x d (ax)(by)
Since all of them are the same base, all of
them can be combined into 1 logarithm. The general rule is, if the log is positive,
it goes up into the numerator;
if the log is negative, it goes down
into the denominator.
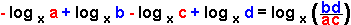
Revisiting the example on the previous page:
log a xy2
It cannot be given a SINGLE coefficient, but can be
expanded into 2 logarithms with different coefficients. Using the reverse of the
addition/subtraction rule above:
| log a (x)(y2) |
= log a x +
log a y2
|
|
= log a x + 2log a y |
Summary
Requirements for combining logs:
- Same base and addition(+)
- Same base and subtraction(-)
- Same base and division(÷)
Requirements for combining numbers in index form:
- Multiplication and same base
- Multiplication and same index
- Division and same base
- Division and same index
Summary of summary
- For combining logs, they must
have the same base and must
not be multiplied.
- For combining index-forms, they must
be multiplied/divided and must
have at least one thing in common
(either index or base) unless being factorized.
Prev Page: Powers
Extended
The Notes Portal Home